9.1.1 歐拉的式子
「哥哥，哥哥！」
又是一個週末，外面寒風陣陣，房間裡卻暖洋洋的很是舒心。
尤里方纔還在安靜地看書，不知怎的忽然站了起來。
我把視線從筆記本上移開，尤里邊摘眼鏡，邊對我露出帶有深意的笑容。
「我說哥哥，你知道『最美的數學公式』嗎？」
「知道啊，歐拉的式子，eiπ= -1 是吧？」
「最美的數學公式」（歐拉的式子）
eiπ= -1
「嘁，你為什麼會知道啊。」尤里的臉上寫著兩個大字——「無聊」。
「因為很有名啊，只要是理科生都知道。」
「是嗎？話說這個數學公式是什麼意思啊？」
「什麼是什麼意思？」
「你看，勾股定理的話就有『直角三角形三邊的關係』，這個歐拉的式子呢？」
「說的也是……」用一句話很難講明白啊。
「比如說，e 是什麼？」
「是自然對數的底，是個著名的常數。e = 2.71828 ... 它是個無理數。」
「沒聽說過。那個，eiπ 的 i 是 i2 = -1 對吧？」
「對，i 是虛數單位。」
「π 是圓周率 3.14 ... ？」
「對，π= 3.14159265358979 ... 是個無限循環的無理數。」
「唔……我最不明白的是 e 的 iπ次方。」
eiπ（什麼意思？）
「嗯，確實。」
「大家都明白這個數學公式的意思嗎？人家不懂啊！」尤里將雙臂交叉在胸前，「很奇怪不是嗎？要是 23 我就明白。二的三次方，連續乘 3 個 2 就好啦，e 也一樣，再怎麼複雜的數字終究還是數字啊。不過 iπ 次方是怎麼回事？難道乘 iπ 個 e 嗎？我不明白。」
「說的也是。」
「說什麼『最美的數學公式』，我還以為是什麼樣的呢，可是人家看了這個 eiπ= -1 的式子也完全不明白什麼意思。沒法說它『美』喵！」
我不知怎的，竟然覺得有些高興。
「尤里真聰明啊……」我想要摸摸她的頭，尤里卻撥開了我的手。
「我說……別隨隨便便摸女孩子頭髮！」
「好好……我們平常看到 23 就會想 到『連續乘 3 個 2』對吧。但是為了理解歐拉的公式，我們必須把這個想法遠遠拋開。這個嘛……因為 eiπ= -1 這個式子屬於『歐拉的公式』的特殊情況，所以可能先學歐拉的公式會比較好。」
「那就教給人家嘛！把 e 乘 iπ 次有意義嗎？」
「雖然需要轉換一下思維，不過還是很有意義的。想聽嗎？」
「嗯！不過人家也能明白嗎？」
「能明白的。只要稍微降低一下嚴謹度，過程應該不是很難。」
我走到房間中央的小桌子前坐下，翻開了筆記本。尤里在我旁邊撲通坐了下來。
我媽敲了敲門走了進來，滿臉忍俊不禁。
「不好意思打攪你們學習了，有位可愛的『跟蹤狂』從剛才開始就在大門前走來走去。是不是你的朋友啊？」
跟蹤狂？
我打開大門，只見一個小個子女生在門口慌亂地踱來踱去。
是泰朵拉。
9.1.2 歐拉的公式
我們回到了我的房間。
小小的桌前，圍坐著我、尤里還有泰朵拉。我媽拿來了紅茶和蛋糕。
「凍壞了吧，別客氣，當自己家就行。」
「您您您您您太客氣了。」
泰朵拉舌頭都打結了，緊張得不行。
「對對對對對不起，我沒想來學長家裡打擾學長，只是偶然路過……」
「沒什麼，剛剛我在跟尤里一起研究數學呢。」
「好久不見，泰朵拉。」尤里打了個招呼。
對哦，她們倆從尤里動完手術出院以後就沒見過了。
兩個人互相對視了一陣子，不一會兒，深深地向對方行了個禮。
喂喂……
「學長在解題嗎？」泰朵拉問我。
「我在解釋歐拉的公式……這就是歐拉的公式。」
◎ ◎ ◎
歐拉的公式（指數函數和三角函數）
這就是歐拉的公式。首先忘記虛數單位 i，先試著看看這個式子。這個式子左邊是指數函數，右邊卻是三角函數。
指數函數是急劇增大的函數。
三角函數是波狀圖像。
在歐拉的公式中，指數函數和三角函數這兩個具有截然不同性質的函數居然被用等號連接了起來。真是奇妙啊。
首先，先說一下能從歐拉的公式推導出歐拉的式子好了。先把歐拉的公式寫在這裡。
將圓周率 π 代入公式，替換公式中的變量 θ。
看之前 y = cos x 的圖像就能得到 cos π 的值了。因為當 x = π 時 y = -1，所以 cos π = -1，由此我們可以得到以下式子。
看 y = sin x 的圖像就能得到 sin π 的值。因為當 x = π 時 y = 0，所以 sin π= 0。
最後，我們用 i × 0 = 0 這個條件。看，得出了歐拉的式子。
也就是說，「最美的數學公式」指的是歐拉的公式中 θ = π 時的情況。
◎ ◎ ◎
「我說哥哥……等一下嘛，歐拉的公式中出現歐拉的式子這點人家能明白，可是人家還是中學生，怎麼會明白指數函數和三角函數什麼的嘛！」
「是是。」
泰朵拉微笑著看著我和尤里。
「哥哥，話說回來，sin x 不是 sin 乘以 x 嗎？」
「呃，不是。sin x 是個函數。加個括號寫成 sin(x) 應該更好理解吧。知道了 x 的值，就知道了與之相對應的 sin x 的值。這就是函數。打個比方，sin 0 的值是 0。意思是當 x = 0 時，sin x = 0。你看 y = sin x 的圖像，是通過 (x, y) = (0, 0) 這一點吧。」
「嗯。」
「同 理，當 
時，sin x = 1，當 x = π 時，sin x = 0。從圖像看得出來吧？」
「嗯……這個是叫正弦曲線吧？」
「沒錯。滿足 y = sin x 的點 (x, y) 的集合就構成正弦曲線。」
「人家明白了啦。」
「那尤里，cos π 的值是多少？」
「不知道。」
「喂喂，看看圖像啊！」
「啊，這樣啊。嗯……cos 這邊是吧。當 x 等於 π 時，縱坐標位於曲線下面啊。是 -1 吧？是吧，cos π = -1。」
「嗯，答對了。尤里你明白了啊。」
「所以人家都！說！了！人家明白了啦！話說回來，人家問的是 eiπ 啊！」
「是是。」
我跟尤里你一句我一句地說著，泰朵拉則靜靜地喝著紅茶。總覺得她跟平時有些不同，似乎在享受這種氛圍般，微微地笑著。
「這房間給人一種很安心的感覺呢。」
9.1.3 指數運算法則
「那我們脫離歐拉的公式，先從基礎的地方開始理解。如果有什麼不明白的，尤里和泰朵拉都可以打斷我。在看到 23（二的三次方）這個數學公式時，我們已經自然而然地會想到指數，即位於 2 右上方的小 3，它表達的是『乘以 2 的個數』。」
「誒，這個弄錯了吧？」尤里問道。
「不，沒弄錯，百分百正確。如果指數是 1, 2, 3, 4, ... 的話，也可以將指數表達為『乘以的個數』。當然，當指數為 1 的時候實際上不能構成乘法運算，這個不用我說吧。」
「嗯。我明白。」尤里回答。泰朵拉也點頭。
「那麼當指數為 0 時會如何呢？ 20 等於多少？」我問道。
「等於 0 吧。」尤里回答。
「應該等於 1 吧？」泰朵拉回答。
「泰朵拉回答正確。20 是等於 1 的。」
20 = 1
「誒？為什麼？明明乘以 0 個，為什麼不是 0 啊？」
「泰朵拉你能解釋一下為什麼 20 = 1 嗎？」
「嗯？讓我來解釋嗎？不好意思，我說不好。」
「這麼想就能理解了，像 24, 23, 22, 21, 20 這樣，把指數逐次減去 1，這樣一來計算結果會有怎樣的變化呢？」
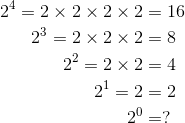
「16 → 8 → 4 → 2，每次都會變成原來的一半呢。」
「對，如果從 2n 的指數 n 減去 1，那麼 2n 的值就會變成原來的二分之一。如果我們從 21 的指數中減去 1，那麼 20 會變成什麼，按照相容性就不用我說了吧。」
「因為是 2 的一半所以……啊，得 1! 原來 20 = 1 啊。」
「是啊。所以我們確定 20 = 1。」
「嗯……不過感覺有點不能接受喵。」
「我也是。聽著聽著就越來越不明白了。就像尤里說的那樣，總覺得乘以 0 個得 1……很彆扭。感覺像是硬加上去的結論……」
「喂喂，你們的思路又回到『乘以的個數』上面去了。我說，只要把指數理解成『乘以的個數』，就不可能理解了。即使理解了，也會覺得是沒理也要辯三分，硬加上去的。只要思維還停留在『乘以的個數』這裡，就沒法逃出自然數的束縛。也就是說，雖然能明白 1, 2, 3, 4, ... 這樣的具體例子，但是像 0 和 -1 這樣一脫離自然數，就會弄不清楚了。」
「尤里能明白 0 個哦！就是『沒有』嘛。」
「不過說到『乘以 0 個』你就搞不清楚了吧。」
「這個嘛，是這樣沒錯……」
「而且，要是說到 -1 個你該怎麼辦呢？」
「-1 個就是借了 1 個嘛，就是這麼回事喵。」
「嗯，這種『解釋』在某些情況下是對的。」我點頭，「但是希望尤里你能明白，『解釋』也是有限度的。0.5 個呢？ π 個怎麼辦？ i 個呢？ iπ 個是什麼意思？對吧。」
「這樣啊……一開始人家就問的這個啊。」
「嗯，所以說，只在自然數的情況下，我們才用『乘以的個數』來思考指數。我們不去強行解釋 0 個和 -1 個的情況，不用『乘以的個數』來定義指數，而是用『數學公式』來定義。我們要站在這個立場去想問題。」
「用數學公式來定義？」泰朵拉和尤里同時提出了疑問。
「對。現在我們要定義 2x 的含義。我們把指數按下面這樣定義，使其滿足指數運算法則。」
指數運算法則
「一般情況下也可以用正數 a > 0 解釋指數運算法則，不過舉出具體數字更容易思考，所以我用 2 來解釋。」
「學長，在講之前我有個問題……」泰朵拉舉起手，「23 的 3 叫作『指數』是吧，那麼 23 的 2 叫什麼呢？」
「叫作『底』，也叫『底數』。」
「泰朵拉你很在乎叫什麼嗎？」尤里問道。
「嗯，非常在乎。這麼重要卻叫不出名字，心裡豈不是很沒底嗎？能叫出名字，不就安心了嗎。尤里你不這麼覺得嗎？」
「嗯，是這樣嗎……」
一直覺得泰朵拉在平時都是一個手忙腳亂的妹妹角色，這麼跟尤里待在一起一對比，感覺她一下沉靜成熟了許多……
「哥哥！繼續繼續！繼續講怎麼用指數運算法則定義指數！」
「比如說我們要研究 20 的值，指數滿足指數運算法則。
2s × 2t = 2s + t
所以，在指數運算法則中代入 s = 1, t = 0，這個等式也成立。不成立就難辦嘍。」
21 × 20 = 21 + 0
「哦……然後呢？」
「計算右邊的指數 1 + 0 = 1，則存在以下等式。
21 × 20 = 21
由指數運算法則我們可知 21 的值，21 = 2。因此可得到如下等式。
2 × 20 = 2
在等式兩邊同時除以 2 的話，20 的值就確定為 1 了。」
20=1
「等一下等一下！」尤里說道，「剛才我們幹了什麼？沒把指數想成『乘以的個數』，直接用指數運算法則定義……嗎？」
「沒錯。」
「原來如此……」泰朵拉點頭，「看著指數運算法則，想辦法讓指數中出現 0，然後由 21 的值確定 20 的值……」
「就是這樣。你們已經成功脫離『乘以幾個 2』的想法了，我們以指數運算法則為基礎確定了要求的值。」
「我想起來了……」泰朵拉說道，「原來聽過 
等於 
。要遵守相容性對吧。嚴格按照指數運算法則算出 0 次方。」
泰朵拉看上去理解得很透徹了。
而尤里卻在抱怨。
「哥哥，剛剛泰朵拉說的我也懂，可是就是接受不了喵……剛剛代入了 s = 1, t = 0 吧，可是就這樣隨便想個值好嗎？用別的 s, t 會不會得出別的值呢……嗯，我說不好……」
我舉起手，示意尤里停一停。
「感覺真敏銳啊……沒事，我明白你想說什麼。你想問指數運算法則究竟有沒有滿足相容性是吧。『定義指數，使其滿足指數運算法則』這點沒什麼問題，但是不是適用於所有指數呢？數學上將這種嚴格適用於所有情況的定義稱為 well-defined。」
「well-defined。」尤里重複了一遍。
「數學領域中要定義什麼的時候，必須證明這個定義是 well-defined 的。不能隨便創造法則，隨便定義概念。這樣就失去相容性了。雖然現在還沒有證明，但指數運算法則是 well-defined 的。」
跟她們講著 well-defined，我想起了米爾嘉說過的話。
「無矛盾性是存在的基石。」
無矛盾性嗎……我剛剛表達為「相容」。這不就是無矛盾性嗎？同樣運用指數運算法則，如果 20 的值一會兒是 1，一會兒是 0，這就矛盾了。可以斷言，像這樣具有矛盾的法則中不能存在 20 這個概念。原來如此……的確，「無矛盾性是存在的基石」。
「Is the term『well-defined』well-defined?」泰朵拉問道。
「什麼？」
「well-defined 這個概念是 well-defined 的嗎……」
「泰朵拉……你到底是何人？」
9.1.4 -1 次方，
次方
「我說，是不是也可以算負數次方啊？」尤里問道。
「我們試試看吧。嗯……假如讓 s = 1, t = -1……」
「不嘛，讓人家來！根據指數運算法則對吧……」
「解出來啦！原來 
啊。」
「嗯，解出來了。」我說。
「學長，這下關於所有的整數 n = ... , -3, -2, -1, 0, 1, 2, ... ，2n 的值都確定了對吧。」
「誒？為什麼啊？」
「因為根據指數運算法則，乘以 21 指數就相應地加上 1，乘以 2-1 指 數就相應地減去 1。」
「啊，這樣啊。之後只要重複就好了。」尤里點頭。
「沒錯。運用指數運算法則，不僅可以算整數的次方，還能算有理數的次方哦。打個比方，我們來算一下 的值。」
「對對， 次方是平方根呢。」泰朵拉說道。
「嗯……最後那裡好像有點奇怪吧？」尤里問道。
「嗯，我沒解釋到位，尤里你居然注意到了……」
「什麼奇怪啊？」泰朵拉重新看了一遍式子。
「這個嘛，在求平方根那裡。」尤里說道。
「對，在求平方根的時候，必須說明 
。因為平方得 2 的數有 
和 
兩個數字。」
「哎呀呀……居然還有條件擋著呢！」泰朵拉說道。
9.1.5 指數函數
「我們的目的是查明歐拉的公式，所以下面稍微加快點速度，從 ex 的微分方程來思考指數函數。」
「微分方程？」尤里問道。
ex 的微分方程
「我們假設指數函數是滿足以上這樣的微分方程的函數。」
「哥哥你一口一個微分方程，人家聽都沒聽過。」
「嗯，說的是啊，不過你等一下，即使不理解微分方程，只要明白這個式子的形式就可以了……為了求指數函數的具體形式，我們像下面這樣，把指數函數寫成冪級數的形式。」
「又出來新詞了……冪級數？」
「詞是很難，不過你只看數學公式就行了。
a0 指的是 x 的 0 次方項，係數是 a0。
a1x 指的是 x 的 1 次方項，係數是 a1。
a2x2 指的是 x 的 2 次方項，係數是 a2 ……
然後，我們把 x 的 0 次方項、1 次方項、2 次方項……這些項無限相加，把這個相加的式子稱為冪級數。我就是想用冪級數的形式表示指數函數。」
「這能行嗎？」
「這個……尤里你這話真犀利啊，不是什麼函數都能用冪級數來表示的。但是關於這點我們先……省略。」
「唔……好吧，就放你一馬。」
「求微分是從函數創造函數的一種方法。用 prime (') 這個符號。關於微分，現在我們只需要考慮兩條法則：第一條法則是，常數的微分結果等於 0；另一條法則是， xk 的微分結果等於 kxk-1。剛才我說的兩條法則可以像下面這樣用數學公式表達。
接著，我們試著把這兩條法則應用到剛才的『指數函數的冪級數』上面。」（其實必須證明微分算子的線性和對於冪級數的可適用性，不過在此就省略了。）
「那個……泰朵拉你明白這些吧？」
「嗯，原來做過一些這方面的題。」
「哇塞！」
「『求微分後形式也相同』指的就是指數函數的微分方程。也就是說，等式 
成立。我們把兩邊都換成冪級數的形式看看。
這樣比較一下等式兩邊的係數，就可以得到以下等式。」
「把它們稍微變個形式，就可以寫成以下這樣。
好好看一下這些等式，確定了 a0 的值，a1 的值也就確定了。確定了 a1 的值，然後 a2 的值也就確定了……就像這樣，跟多米諾骨牌一樣一個個確定值。那麼 a0 是什麼？實際上考慮一下 ex 的冪級數，就不難確定 a0 的值了。
代入 x = 0，就可以消去 a1x + a2x2 + a3x3 + ... 中含有 x 的部分了。因為我們已知在微分方程中 e0 = 1，所以……
也就是說 a0 = 1。既然確定了 a0……」
「因為在這裡 
可以用階乘表示為 k!，所以可得以下等式。
這是將指數函數 ex 泰勒展開得到的冪級數。在此，我們明確寫出 x0 和 x1 的指數和前面的符號 +，再把 0! 看作 1，用簡明易懂的形式表示出來。」
指數函數 ex 的泰勒展開
9.1.6 遵守數學公式
「那麼，接下來到指數函數的高潮部分嘍。」
「喔？」
「剛才我們丟掉了『指數表示的是乘以的個數』這個概念對吧，取而代之，我們把它理解成遵守指數運算法則這個數學公式的數字。從數學公式具有的相容性出發，延伸指數的含義。這次我們再重複一遍剛才的工作，也就是說利用數學公式來定義指數函數。怎麼辦呢？我們把剛才的泰勒展開——
進行『指數函數定義』。」
「咦？人家不太明白呢。我說哥哥，不是之前有過指數函數，我們已經把它泰勒展開了嗎？」
「對。確實是這樣。不過在泰勒展開的時候，指數函數 ex 的 x 畢竟還在實數範圍內。現在我們想在指數函數 ex 的 x 裡加入複數，所以要利用泰勒展開得到的冪級數這種數學公式的形式，來定義指數函數。」
「喔？」
「還記得歐拉的公式左邊是什麼樣子吧？」
對吧？為了求出 ，我們在指數函數的冪級數中代入 x = iθ。這可以說是出於對數學公式的信任而進行的『大膽的代入』。
代入 x = iθ，再利用 i2 = -1，則 1 → i → -1 → -i → 的循環就派上大用場了……」
「啊啊啊啊啊啊！」泰朵拉沉默了好一會兒，突然爆發了。
「咋了咋了咋了？！」尤里也跟著大叫起來。
「什麼事啊？！」我媽趕過來了。
為什麼連老媽都過來了啊……
「對不起對不起，沒什麼。我只是有點吃驚……」泰朵拉紅了臉。
9.1.7 向三角函數架起橋樑
「泰朵拉，什麼讓你那麼吃驚啊？」尤里問道。
「我知道 cos θ 和 sin θ 的泰勒展開。」
「不愧是高中生。」
「不，只是學長……私下有教過我。」
尤里一瞬間露出了不開心的表情，不過馬上就恢復了原樣。
「cos θ 和 sin θ 的泰勒展開是什麼樣子的？」
「是這樣的。」
cos θ 的泰勒展開
sin θ 的泰勒展開
「喔？然後呢？」尤里問道。
「尤里你不覺得很吃驚嗎？」
「為什麼要吃驚啊？」
「因為歐拉的公式不是已經出來了嗎？」
「誒？」
「你看，cos θ 是 0, 2, 4, 6, ... 這樣，只出現了偶數對吧。而 sin θ 是 1, 3, 5, 7, ... 這樣，只有奇數對吧？」
尤里似乎還不太明白。
「就是這樣。」我說，「泰朵拉先注意到了。總之，先好好看看指數函數 ex 和三角函數 sin θ，cos θ 的泰勒展開，然後歐拉的公式就會出來了。」
「誒？光用說的人家怎麼能明白嘛，要寫出來解釋給人家聽嘛～」
「好好……」
◎ ◎ ◎
好好……那麼首先寫出 ex 的泰勒展開。
然後，代入 x = iθ（大膽地代入）。
計算 
。
然後利用 i2 = -1，只留下奇數次的 i。這時也得注意符號。
接下來把 θ 的偶數次項和奇數次項分開羅列。
明白了嗎？在指數函數 ex 的冪級數中代入 x = iθ，然後就把 θ 的偶數次項和奇數次項分開了。雖然和泰朵拉寫的三角函數的泰勒展開一對比就明白，不過「θ 的偶數次項」是 cos θ 的泰勒展開，而「θ 的奇數次項」是在 sin θ 的泰勒展開中乘了一個 i。把它們加在一起，歐拉的公式就出來了。
雖然略去了很多需要嚴謹討論的部分，不過總算完成了。如何，尤里？
◎ ◎ ◎
「如何，尤里？」
「嗯……」尤里皺著眉頭認真地思考著，「我說哥哥，這次講的歐拉的公式，人家還沒有完全明白。就這樣突然跳到指數函數、三角函數、微分方程太難了啦。人家感覺腦子都快炸了啦。」
尤里雙手盤在胸前，繼續說著。
「不過啊，也有人家能明白的部分，就是 eiπ 的意思。在聽哥哥講以前我都一直覺得，iπ 次方肯定沒有意義！因為我一直認為指數就是『乘以的個數』。是泰朵拉說的吧，沒理也要辯三分，硬加上去的。不過聽哥哥用冪級數講過以後，人家才明白自己之前都錯了。這不是硬加上去的，不是用『乘以的個數』來定義指數，而是用指數運算法則這個數學公式來定義。還有，指數函數 ex 也是用冪級數這個數學公式定義的。」
尤里用力地點了好幾次頭，馬尾辮配合著頭部的擺動搖晃著。
「尤里真聰明！居然能明白這麼多！」我忍不住讚歎。
「學長，剛才尤里一說我也感覺到了。」泰朵拉說道，「用指數運算法則定義，還有用冪級數定義，學長都非常重視數學公式呢。」
「嗯，就是這樣。可以說是『信賴數學公式』。」
「還有學長……我覺得冪級數特別厲害。居然能把像指數函數和三角函數這樣看上去完全沒有聯繫的事物聯繫在一起。這也可以說是很大程度上的同等看待吧。冪級數在指數函數和三角函數之間架起了橋樑。」
「確實如此。」我表示同意，「虛數單位 i 也很有趣。光是知道 i2 = -1，像這樣列出
就會得到 1, i, -1, -i 的循環。
這正好與『形成 90° 旋轉，週期為 4』『x4 = 1 的解變成 x = 1, i, -1, -i』『三角函數的微分週期變成 4』……這些條件相呼應。」
「原來如此……」泰朵拉露出佩服的表情。
「我們也從幾何層面考慮看看吧。在復平面上畫一個以原點為中心的單位圓……」
「將幅角設為 θ，這樣一來這個單位圓上的點就對應 cos θ + i sin θ 這個複數。根據歐拉的公式 
，可以確定圓上的點與複數 對應。也就是說，『最美的數學公式』 —— 歐拉的式子 包含了
『單位圓上，幅角為 π 的複數等於 -1』
這個含義。這就是尤里之前的問題的答案即『歐拉的式子的含義』。」
「學長……也就是說，歐拉的公式就是『面朝右的人向後轉，就會面朝左』是嗎？」泰朵拉左右搖著頭說道。
「這個嘛，可以這麼說……」我不禁苦笑。
「嗯……感覺好像明白了，我明白這是有道理的了……」尤里說道。
這時，我媽從門口探出了臉。
「孩子們，先休息一下，過來喝個茶再學怎麼樣？」
「知道了，這就去。」
「我等你們哦。」說著我媽縮回了身子。
回到單位圓。
「然後，把 θ 持續增大，與複數 相對應的點就會在單位圓上來迴旋轉。每當角度 θ 增加 360°，也就是增加 2π 弧度的時候，點會轉回到同一個地方，也就是說有週期性。我們試試用數學公式來證明！」
「看，確認了週期性。幅角 θ + 2π 的複數等於幅角 θ 的複數。」
「感覺全部都相關聯呢……」泰朵拉說道。
「我說哥哥！雖然人家剛剛才學，這麼說可能有點太自以為是了……或許歐拉的式子 很美，不過我更喜歡歐拉的公式。
嗯，我非常喜歡歐拉的公式。雖然人家還不太理解，不過這一行數學公式中居然包含了這麼多美麗的東西。歐拉真是了不起喵！」
「嗯，是很了不起。」我表示贊同。
「我說尤里，跟哥哥道個謝吧？」
「說的是啊，謝謝哥哥。」
「多謝學長經常教我們數學。」
「沒什麼沒什麼，你們經常聽我講，我才要謝謝你們。」
我媽又從門口探出了臉。
「你們都不過來，我這當媽的有點寂寞啊……」
「這就過去。」尤里答道。