8.3.1 旅行的出發點：用 m, n 表示 A, B, C, D
夜晚，在自己家裡。
我即將要出發去旅行，一場推導矛盾的旅行。已確認出發地點。自然數 A, B, C, D 有著如下關係。就從這裡開始推導矛盾。
出發點
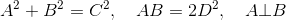
由 A2 + B2 = C2 和 A ⊥ B，可知 A, B, C 是一組基本勾股數。也就是說，採用『基本勾股數的一般形式』，就可以用 m, n 表示 A, B, C。這就是泰朵拉所說的畢達哥拉·搾汁機。
基本勾股數的一般形式（畢達哥拉·搾汁機）
自然數 m, n 的條件：
m > n
m ⊥ n
m, n 僅有一方為奇數（兩者奇偶性不一致）
（參考 2.5 節）
由「面積是平方數」這個條件我們已經推導出了 AB = 2D2 這個等式，接下來將 m, n 代入這個等式，研究 D 的性質。
之前雖然跟泰朵拉講了定義方程式的作用，但自己面臨導入變量的時候，心中還是會有一絲不安。我很擔心，會不會增加變量後搞得一團亂呢……
我告訴自己「要信賴數學公式」，趕走了心中不安的情緒。數學公式的好處就在於，可以脫離含義，用機械性的操作來一層層解開問題。只要將基本勾股數的一般形式納入式子中，就可以忘掉直角三角形的事兒了。之後勝負就取決於能否將數學公式作為武器熟練運用了。
首先用 m, n 表示 AB = 2D2。
雖然看不到路途前方有什麼，但旅行開始了。
上路吧！
看，出現了這樣的等式。
D2 = mn(m + n)(m - n)
這不是……之前做過的形式嗎？
左邊的 D2 是「平方數」。
然後，右邊是「互質數字的乘積」，沒錯……吧？
因為 m 和 n 互質，所以從這裡出現的四個因子
m, n, m + n, m - n
中，任意拿出兩個因子，都可以兩兩互質……是吧？
比如說，存在 (m + n) ⊥ (m - n) ？
我很不安。
如果在這裡不存在 (m + n) ⊥ (m - n)，我就失去了重要的武器。用反證法踏踏實實地證明吧。
假設 m + n 和 m - n 不互質，此時應存在某個質數 p 和自然數 J, K 使得下式成立。
這個質數 p 是 m + n 和 m - n 共同的質因數。
只要從這個式子推導出矛盾，就能證明 m + n 和 m - n 互質了。來，看看能不能守住武器。
把上面兩個式子左右兩邊分別相加，導出 p 和 m 的關係。
將左右兩邊分別相減，導出 p 和 n 的關係。
於是得到以下關係。
變成了乘積的形式，我已經明白了！
首先，p 不可能等於 2。因為 m 和 n 的奇偶性不一致，所以 pJ = m + n 是奇數，因此 p 不是偶數。也就是說，p 不可能等於 2。
但是 p 也不可能大於等於 3。因為如果 p 大於等於 3，m 和 n 就都是 p 的倍數。但是 m ⊥ n —— 也就是說 m 和 n 沒有共同的質因數。所以 p 不可能大於等於 3。
綜上所述，可以說 (m + n) ⊥ (m - n)。
呼……
以防萬一，我把 m + n 和 m 互質的關係也寫出來吧。
假設 m + n 和 m 不互質，此時存在某個質數 p 和自然數 J, K 使得下式成立。
採用跟剛才同樣的方法，得到如下等式。
據此可知 m, n 都是 p 的倍數，和 m ⊥ n 相矛盾。
同理可證 m - n 和 m，m + n 和 n，m - n 和 n 都互質。
好，這樣就證明了四個因子
m, n, m + n, m - n
是分別兩兩互質的。我牢牢守住了重要的武器。
那麼言歸正傳。剛剛經研究得出了下式。
D2 = mn(m + n)(m - n)
一方面，左邊的 D2 是平方數。如果進行質因數分解，就能得到 D2 含有偶數個質因數。
另一方面，右邊四個因子 m, n, m + n, m - n 是兩兩互質的 —— 也就是說沒有共同的質因數。
想像一下把左邊的質因數分配到右邊四個因子中的情況，則四個因子都各自含有偶數個質因數。總之一句話，「m, n, m + n, m - n 全部是平方數」！
「互質」真的是一件實用的武器啊……用「最大公約數為 1」體現「互質」的時候還有些摸不清狀況，而換成「沒有共同的質因數」就感覺一下子開竅了，就如同一把鋒利的長劍。
8.3.2 原子和基本粒子的關係：用 e, f, s, t 表示 m, n
接下來用數學公式來表示 m, n, m + n, m - n 是平方數這個條件吧。
剛才我們用 m, n 表示了 A, B, C, D。
這次用 e, f, s, t 表示 m, n。
嗯？
我……
我難不成踏上了發現微結構的旅途？
研究原子 (A, B, C, D)，發現了小原子 (m, n)。
研究原子 (m, n)，又發現了更小的基本粒子 (e, f, s, t)……
這次的旅行就是這麼回事吧。
沒準還有更小的夸克……
接下來……
因為 m, n, m + n, m - n 是平方數，所以存在以下自然數 e, f, s, t。
用 e, f, s, t 表示 m, n, m + n, m - n「原子和基本粒子的關係」
e, f, s, t 分別兩兩互質。
又導入了新的變量，而且還是四個……不過一定沒問題的。要信賴數學公式，信賴數學公式……
下面該往哪邊走呢？我重看了一遍筆記想著。
試試用 e, f, s, t 表示 m 吧。雖然已經有 m = e2 這個等式了，不過由下面的式子應該能夠得到些什麼。
嗯，把兩個式子左右兩邊分別相加相減，可以用 s, t 表示 m, n，即用基本粒子來表現原子的結構。
根據「兩數之和乘以兩數之差等於平方差」，將 2n=s2 - t2 的右邊變形為乘積的形式。做出乘積的形式，是為了方便研究整數的結構。
可得到 f 和 s + t, s - t 的關係，即基本粒子間的關係。
f 和 s + t, s - t 的關係「基本粒子間的關係」
2f2 = (s + t)(s - t)
8.3.3 研究基本粒子 s + t, s - t
下面來研究剛才得出的式子 2f2 = (s + t)(s - t)，先從等式右邊的因子 s + t, s - t 開始吧。
s + t 和 s - t 是整數。首先「調查奇偶性」。
s 的奇偶性如何呢？根據「原子和基本粒子的關係」，可知存在 m + n = s2。m + n 的奇偶性……我懂了。因為 m 和 n 的奇偶性不一致，所以 m + n 不是偶數 + 奇數就是奇數 + 偶數。不管怎樣，m + n 都是奇數，也就是說 s2 也是奇數。s 平方後還得奇數，說明 s 也是奇數。好，明確 s 是奇數了！
t 的奇偶性同理。存在 m - n = t2，m 和 n 的奇偶性不一致。t2 是奇數，因為 t 平方後還得奇數，所以 ((t 也是奇數((。
因此，s 和 t 都是奇數 —— 就是它！
因為 s 和 t 都是奇數，所以 s + t 和 s - t 都是偶數。
話說回來，s 和 t 互質嗎？
因為 (m + n) ⊥ (m - n)，所以 s2 ⊥ t2。因為平方後的數字互質，所以平方前的數字也互質。沒有共同的質因數這點在平方前和平方後是不變的。也就是說，s 和 t 是互質的。
好，這樣就明確了 s ⊥ t ！
咦？我不是在「原子和基本粒子的關係」中以「e, f, s, t 分別兩兩互質」為前提導入了變量嗎……算了，總之可以肯定 s ⊥ t。
這樣 s，t 就基本摸透了。
由 s, t 可知
s 是奇數
t 是奇數
s + t 是偶數
s - t 是偶數
s 和 t 互質(s ⊥ t)
我又看了一遍筆記，考慮應該把剛剛得到的 s + t 和 s - t 的條件代入哪個式子。
帶有 s + t 和 s - t 這樣的因子的數……在這個「基本粒子間的關係」中。
2f2 = (s + t)(s - t)
因為 s + t 和 s - t 是偶數，所以 
和 
是整數。上式可寫成下面這樣。
寫成這樣後，右邊就成了四個整數的乘積的形式。
在等式兩邊同時除以 2，得到
左邊是平方數……慢著，誒？我剛才不也做了一樣的事嗎？這不是又繞回原路了嗎？
不不，不要緊。等式左邊的 f2 是平方數，右邊含有質因數 2。因為等式右邊應該也是平方數，所以另一個質因數 2 應該分配給兩個因子中的一個，即 和 中的一個。
也就是說， 和 之中有一個是偶數。
和 是不是互質的呢？
打比方說，假設 和 不互質……類似這種檢驗已經做了無數回了吧。設它們有共同的質因數 p，則存在整數 J, K，它們之間的關係可以用下式表示。
將等式左右兩邊分別相加，分別相減，得到下式。
明白了。由以上等式可知，s 和 t 都是 p 的倍數。因為 s 和 t 都有共同的質因數 p，所以這與 s ⊥ t 相矛盾。因此可以得出結論： 和 互質。
， 和 中有一方是偶數， 和 還是互質的……因為沒有共同的質因數，所以一方為偶數的話，另一方就為奇數。
這就意味著，像往常一樣考慮分配質因數的話……偶數是「2 × 平方數」的形式，奇數則是「奇數的平方數」的形式。
用語言表達可能有些複雜。再導入構成「基本粒子」s, t 的「夸克」u, v 怎麼樣？設 u, v 是互質的自然數。
這樣一來，「2 × 平方數」就能寫成 2u2，「奇數的平方數」就能寫成 v2 了。
和 中有一方是 2u2，另一方是 v2。
呼……
8.3.4 基本粒子和夸克的關係：用 u, v 表示 s, t
就快受不了像洪水一樣氾濫的字母了。我又慢慢地把筆記啃了一遍，就夸克進行了一下整理。
關於
u 和 v 是互質的(u ⊥ v)。
v 是奇數。
很好，不錯不錯！ 不，糟了！
只有這點條件，根本分不出 ， 裡誰是 2u2 誰是 v2。這就意味著……要分情況討論。
我抱著頭發愁。
情況 1：當 
時——
情況 2：當 
時——
變成分情況討論了。
我呆呆地站在森林深處的分岔口處。
確實可以兩條路都走。
不過，這樣的話就得花兩倍時間和精力了。
嗯……有沒有什麼好辦法呢？我再一次回首向走過的路望去，看看有沒有忘掉哪個關係式。
嗯？
m 呢？完全沒有用到在「原子和基本粒子的關係」裡出現的 m = e2 啊。m 應該和基本粒子 s, t 相關聯才對啊！嗯……將關係式
左右兩邊分別相加再除以 2，可得
由此，可得出下式。
也就是說，下式成立。
很好，將 s 和 t 分別平方後再相加，就可以把情況 1 和 2 總結成一個式子了！這樣就避免了分情況討論！
哇！整理出了一個相當簡單的等式，這就是基本粒子 e 和夸克 u, v 的關係式。不錯不錯……
誒？話說回來，我高興個什麼勁兒啊？
怎麼能因為成功變形了幾個等式就高興呢！我想要的是——找出矛盾。
接下來會出現矛盾嗎？
「基本粒子 e 和夸克 u, v 的關係」（接下來會出現矛盾嗎？）
u ⊥ v
v 是奇數
嗯，雖然很不甘心，但已經困得不行了。
今天就到這裡吧……