萊昂哈德·歐拉於1783年辭世,這一年距萊布尼茨發表第一篇微積分論文一百週年僅差一年。無論按什麼標準衡量,這一百年都是數學史上非同尋常的一個世紀。到目前為止我們考察的結果雖然只是這個世紀獲得的豐碩成果中的一小部分,卻說明已經有了巨大進展。牛頓、萊布尼茨、伯努利兄弟和歐拉致力於無窮量研究,發現了大量正確的而且時常是驚人的結果,同時確立了微積分作為數學中的典範學科分支的地位。讓我們不由得對這些開拓者們肅然起敬。
頭一個世紀的一個重要的發展趨勢是人們把視點從幾何轉向分析。當問題變得越來越棘手時,它們的解對曲線幾何性質的依賴越來越少,而對函數代數運算的依賴卻越來越多。萊布尼茨在1673年證明他的變換定理所用的複雜的幾何圖解在18世紀中期歐拉的著作中已經無影無蹤了。從這個意義上說,分析學已經具備了更現代的形態。
但是這門學科的其他常見內容卻銷聲匿跡了。例如,很大的一個缺失是現代分析學的支柱——不等式。17世紀和18世紀的數學家們主要處理等式。他們的工作傾向於利用巧妙的代換將一個公式變換成另一種想要的形式。雖然雅各布·伯努利對調和級數發散性的證明(見第3章)是以熟練地運用不等式為特徵,但是這樣的例子總體上是罕見的。
同樣稀少的是對廣泛函數類的分析。歐拉和他的前輩們擅長研究特定的積分或級數,但是他們對連續函數或可微函數這樣的函數類的一般特性缺乏興趣。把關注的焦點從特殊的函數轉移到一般的函數將成為下一個世紀的標誌。
早期微積分和當今微積分的另外一個顯著差異是對邏輯基礎的關注不同。正如我們所見,那個時期的數學家在使用結果時既不證明它們的正確性,在許多情況下,甚至也不考慮這個問題。一個例子是用積分的無窮級數代替無窮級數的積分的這種趨勢,也就是說,把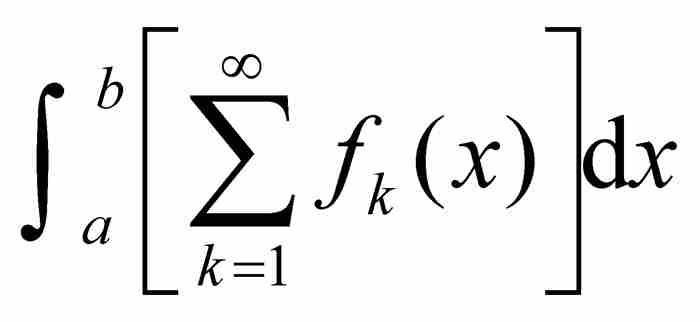 和
和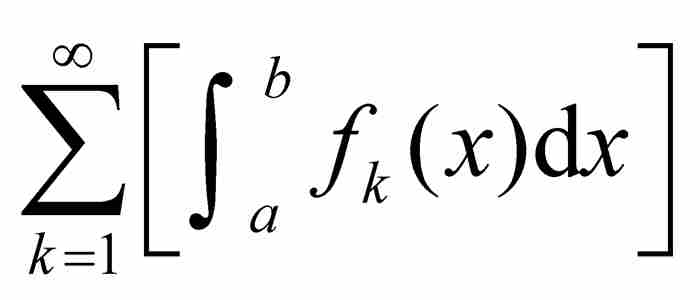 看成是相等的。這裡的兩種運算(對函數積分和對級數求和)都包含無限的步驟,這種不加區別的交換可能會導致錯誤結果。只有在滿足某些條件時這種交換才是可行的。在這方面,微積分的先驅們多半依靠直覺而不是根據推理進行運算。不可否認,他們的直覺通常是非常可靠的。特別是歐拉,他具有一種神奇的能力,在他陷入數學的深淵之前就準確知道自己可以走多遠。
看成是相等的。這裡的兩種運算(對函數積分和對級數求和)都包含無限的步驟,這種不加區別的交換可能會導致錯誤結果。只有在滿足某些條件時這種交換才是可行的。在這方面,微積分的先驅們多半依靠直覺而不是根據推理進行運算。不可否認,他們的直覺通常是非常可靠的。特別是歐拉,他具有一種神奇的能力,在他陷入數學的深淵之前就準確知道自己可以走多遠。
然而,微積分的基礎依舊是令人懷疑的。作為一個例證,我們不妨回憶一下無窮小量所扮演的角色。為了解釋這些稱為無窮小的量,從萊布尼茨到歐拉,他們都作過嘗試,但是從來沒有給出令人滿意的證明。像一條數學變色龍,無窮小看起來不可避免地同時既是零又不是零。從根本上說,它們的存在似乎是自相矛盾和違背直覺的。
數學家們將他們的結論建立在「逐漸消失的」量上不是什麼好事。牛頓是這種動態方法的倡導者,對於醉心於運動研究的他來說,這或許是一種合理的主張。在引入我們現在所謂的導數的時候,他考察了逐漸消失的量的商,並且寫道,他所指的這些逐漸消失的量的「最終比」,「既不是在它們消失之前的比,也不是在消失之後的比,而是正當這些量消失時的比」。1 除了想像一個量在消失(無論含義是什麼)之後的概念以外,牛頓還要求他的讀者想像當分子和分母噗的一聲同時消失在稀薄空氣中時的比。他的描述看起來給予非難者以可乘之機。
1 Dirk Struik(ed.), A Source Book in Mathematics, 1200-1800, Harvard University Press, 1969, p.300。
批評很快來臨,而批評者是喬治·伯克萊(1685—1753)——英國著名的哲學家和克羅因教區的主教。伯克萊在他1734年所寫的《分析學家》一文中,嘲笑那些遣責他依靠宗教信仰而不是理性行事的科學家們自己也在談論著無窮小的量或逐漸消失的量。對伯克萊來說,這是最模糊的思想和最虛偽的行為。這一點隱含在文章長長的副標題中:
——致一位不信教的數學家的評論,其中剖析現代分析學的目標、原理和結論是否比宗教的神秘和教義有更清晰的構思或更縝密的推理。2
2 George Berkeley, The Works of George Berkeley, vol. 4, Neison & Sons, London, 1951, p. 53。
伯克萊的評論非常刻薄。對於這位主教來說,無論微積分是建立在牛頓的逐漸消失的量的概念上還是建立在萊布尼茨的無窮小的概念上,都沒有多大差別。他得出結論:「越是用心分析和追尋這些虛無飄渺的思想,越發陷入糊塗與迷茫的深淵。」3 伯克萊以拷問牛頓的口吻,提出了當時聞名遐爾的質疑:
這些流數到底是什麼?逐漸消失的增量的速度有多麼大?這些相同的逐漸消失的增量是什麼?它們既不是有限的量,也不是無窮小的量,更不是零。難道我們不能把它們稱為消逝的量的鬼魂嗎?4
3 George Berkeley, The Works of George Berkeley, vol. 4, Neison & Sons, London, 1951, p. 67。
4 George Berkeley, The Works of George Berkeley, vol. 4, Neison & Sons, London, 1951, p. 89。
伯克萊對萊布尼茨的無窮小量的概念也毫不客氣。他嘲諷道,承認一個無窮小量的概念超出了「我的能力」,接受像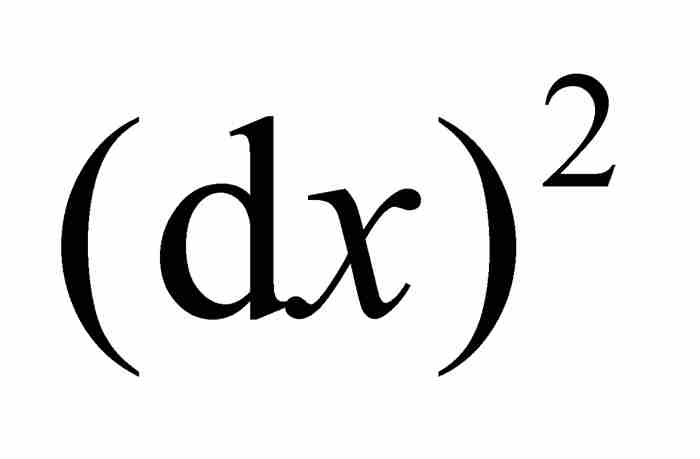 這樣的無窮小量的無窮小部分「對任何人而言都是無限困難的」。5
這樣的無窮小量的無窮小部分「對任何人而言都是無限困難的」。5
5 George Berkeley, The Works of George Berkeley, vol. 4, Neison & Sons, London, 1951, p. 68。
伯克萊並沒有對數學家們從這些可疑的方法推出的結論提出質疑,他拒絕的是這些結論背後的邏輯。事實上,微積分是求切線和確定極大值或極小值的極好工具。但是,他爭辯說,它的正確答案來自錯誤的思想,正如在某種錯誤補償中某些錯誤抵消其他錯誤,從而掩蓋其中隱藏的漏洞。他寫道:「錯誤也許能產生真理,但是決不會產生科學。」6
6 George Berkeley, The Works of George Berkeley, vol. 4, Neison & Sons, London, 1951, p. 77。
我們借助伯克萊的例子來說明他的觀點,使用現代符號表示就是,當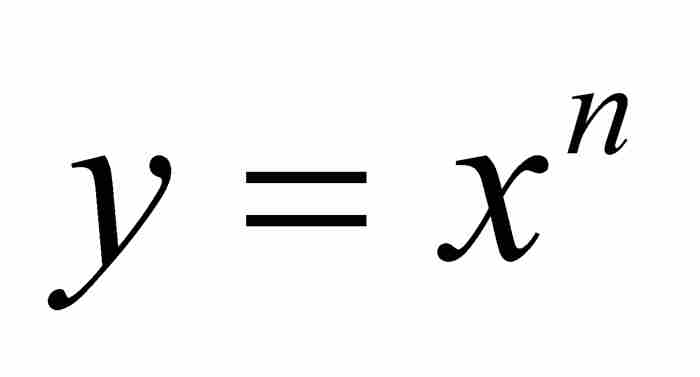 時,求
時,求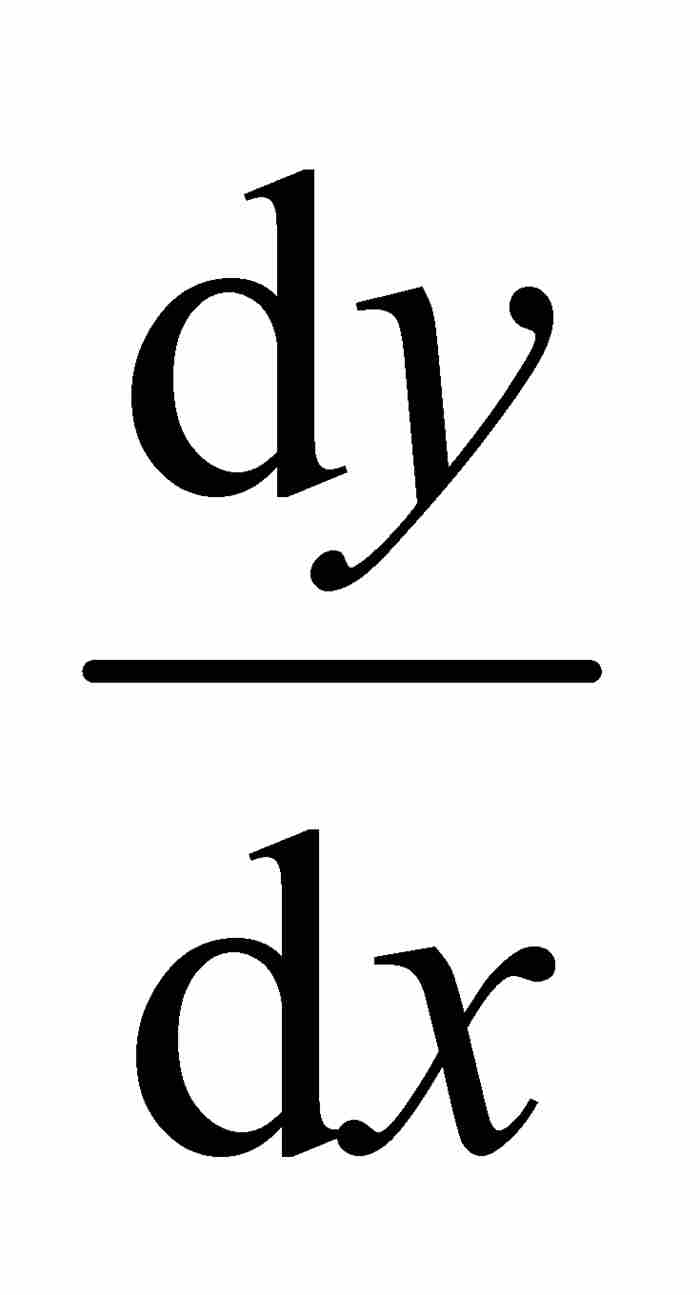 。按照當時的方式,他先對 x 增加一個微小的非零增量o,然後求微商
。按照當時的方式,他先對 x 增加一個微小的非零增量o,然後求微商
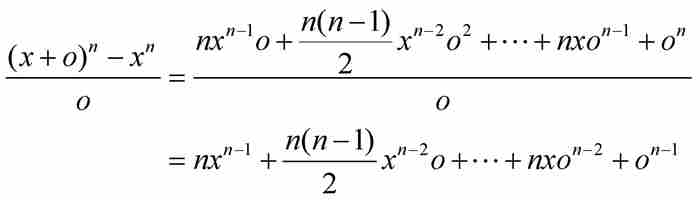
到這一步為止,o依然被假設為一個非零的量,伯克萊強調:「如果沒有這個條件,我就不能在下一步推出任何結果。」但是,隨後o忽然變成了零,所以
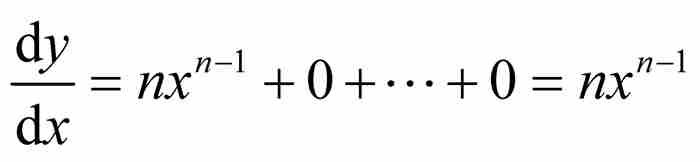
伯克萊不贊成的是第二個假設與第一個假設完全衝突,因此他否定由此推出的任何結論。畢竟,如果o是零,我們不僅不能把它作為分母,而且必須承認x根本就沒有增加。所有的論據立刻土崩瓦解。伯克萊寫道:「當提到讓增量消失時,前面那個增量為某種量的假設就被破壞了,然而,由這個假設所推出的結果,即由它獲得的表達式卻保留了下來。」7
7 George Berkeley, The Works of George Berkeley, vol. 4, Neison & Sons, London, 1951, p. 72。
對這位主教來說,這種推理方法是完全不能接受的,並且是「一種極端自相矛盾的討論方式,而這種方式在上帝那裡是不允許的」。8 在《分析學家》最具火藥味的一段話中,伯克萊對比了他所說的微積分的錯誤邏輯與人類知識要求的高標準,「我相信在人類所有知識門類的任何一種知識中,人們都不會承認像在數學證明中所接受的這種推理」。9
8 George Berkeley, The Works of George Berkeley, vol. 4, Neison & Sons, London, 1951, p. 73。
9 George Berkeley, The Works of George Berkeley, vol. 4, Neison & Sons, London, 1951, p. 74。
伯克萊主教充分闡明了他的觀點。即使微積分的結果似乎是正確的,並且當應用於像力學或光學中的實際現象時,得到的解答也和觀測結果一致,但是,如果基礎不牢的話,這種結果依然一錢不值。
必須做些事情了!在其後的數十年中,很多數學家試圖加固微積分搖搖欲墜的基礎結構。讓·勒朗·達朗貝爾(1717—1783)就是其中的一員。他是一位備受尊敬的學者,與德尼·狄德羅(1713—1784)一起在法國編纂《百科全書》。對於微積分的基礎,達朗貝爾同意無窮小量或者逐漸消失的量是沒有意義的。他毫不含糊地宣稱:「一個量或者是有,或者是沒有。如果是有,它就還沒有消失;如果是沒有,它就確實消失了。假設存在介於這兩者之間的中間狀態,就只能是一頭由獅頭羊身和蛇尾構成的吐火怪物。」 10
10 Carl Boyer, The Concepts of the Calculus, Hafner, 1949, p. 248。
相反,達朗貝爾提出了建立在「極限」概念基礎之上的微積分。在處理導數時,他把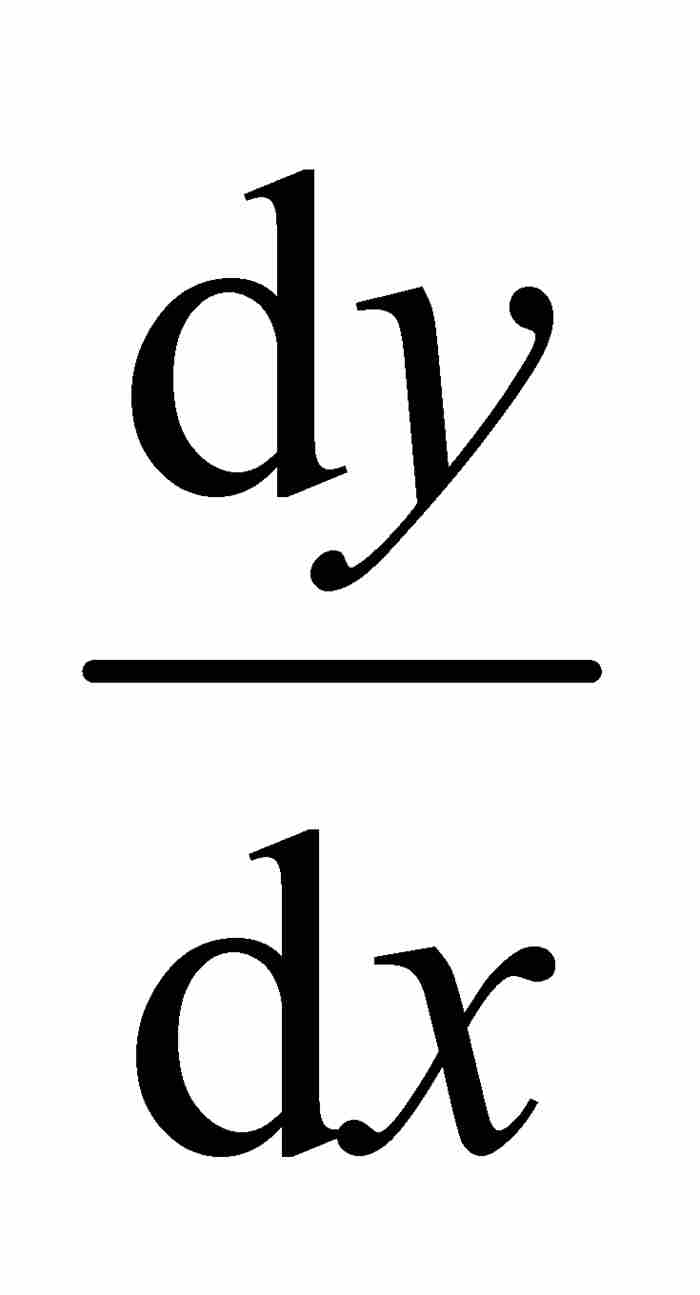 看成是有限項的商的極限。他將這個商表示為
看成是有限項的商的極限。他將這個商表示為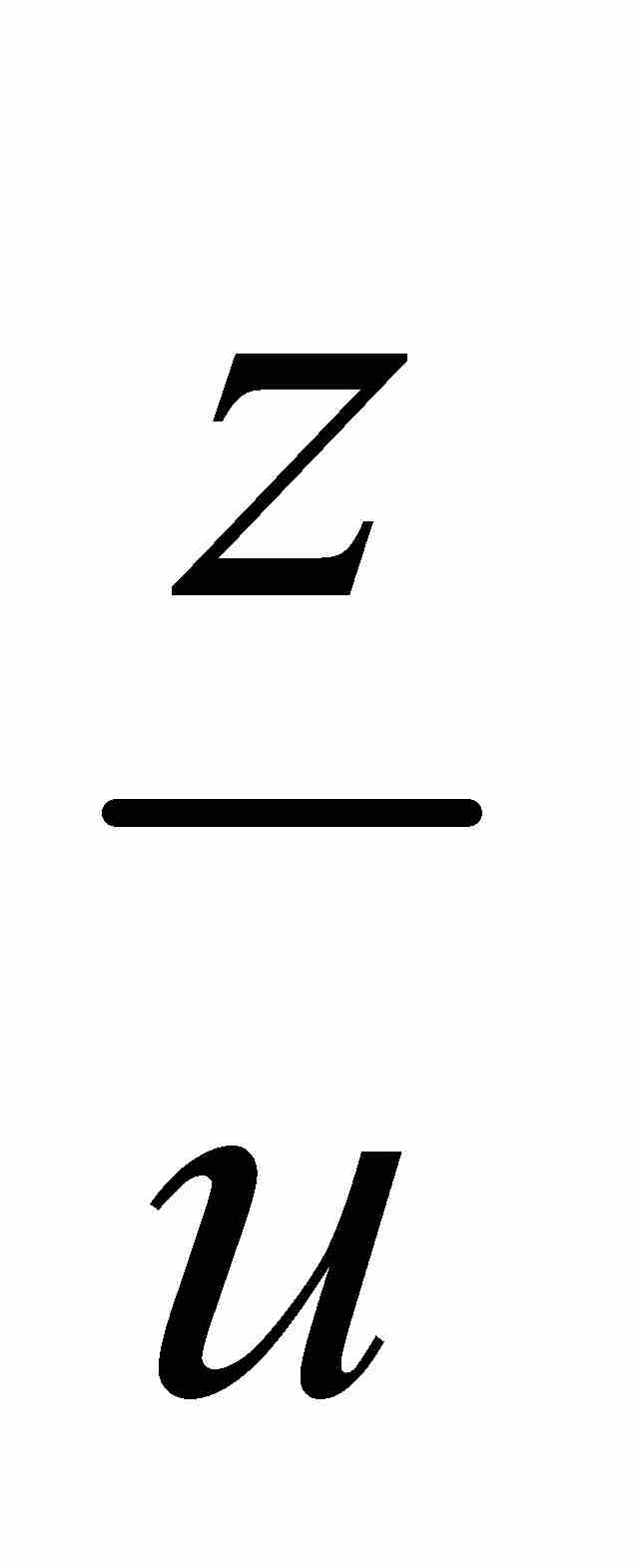 ,而我們現在認為是
,而我們現在認為是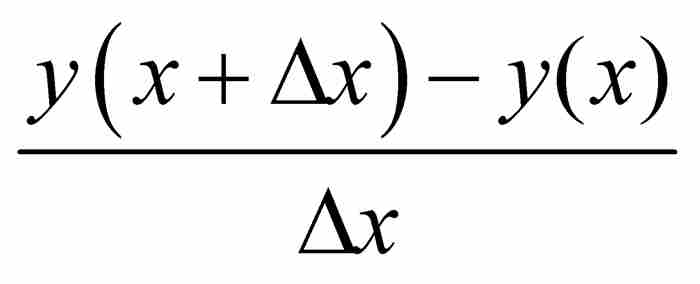 。那麼,
。那麼,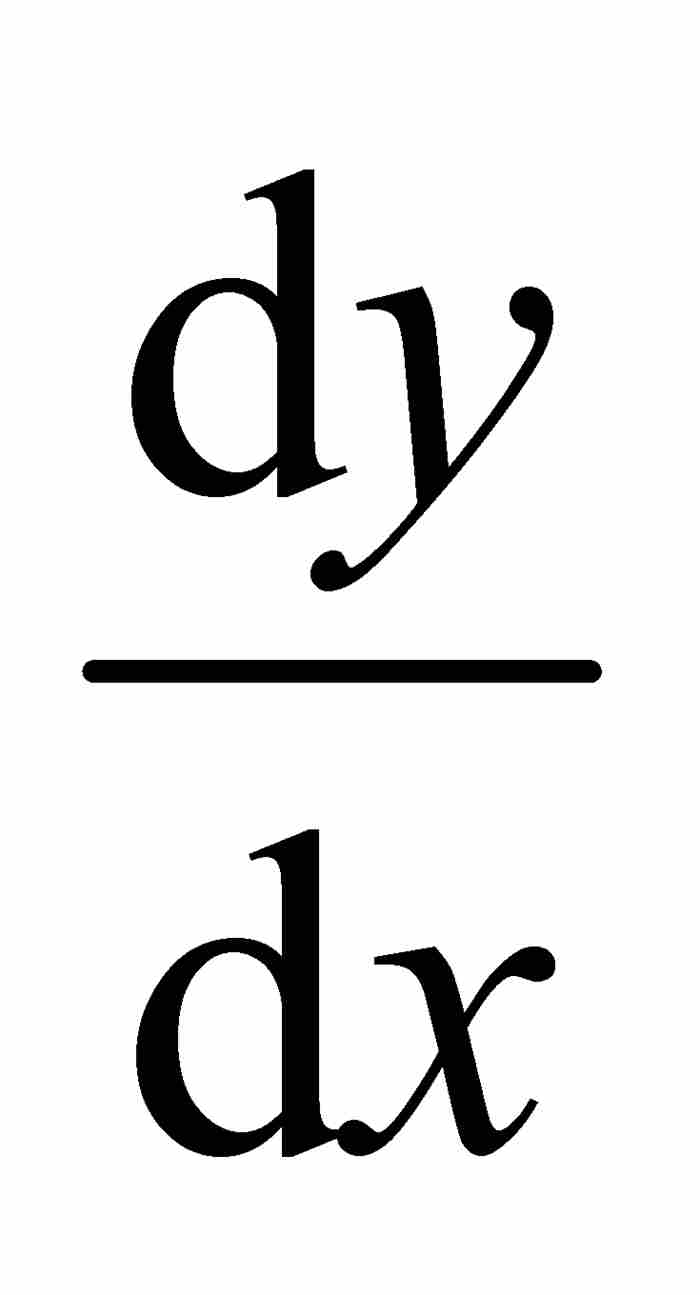 是「在我們假定z和u為實數並且不斷減小時,比值
是「在我們假定z和u為實數並且不斷減小時,比值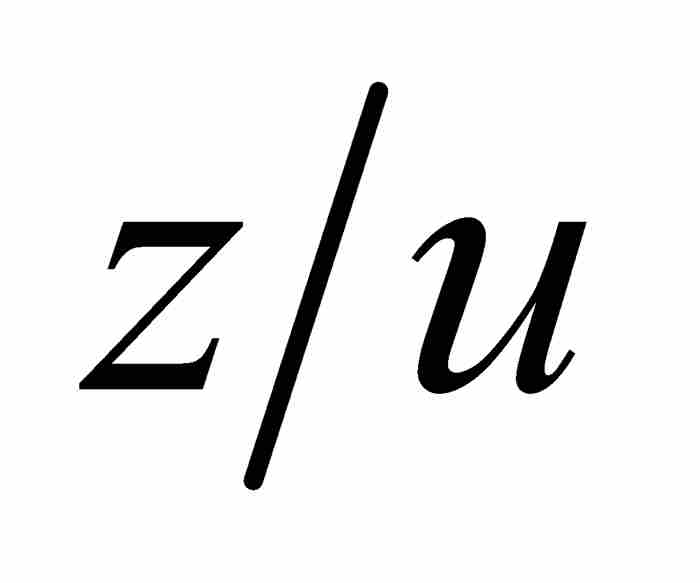 越來越接近的量。沒有比這更清楚的定義了」。11
越來越接近的量。沒有比這更清楚的定義了」。11
11 Dirk Struik(ed.), A Source Book in Mathematics, 1200-1800, Harvard University Press, 1969, p. 344。
達朗貝爾取得了某些進展。他沒有使用無限小,也沒有使用逐漸消失的量,並且由於突出極限作為修補微積分薄弱基礎的方法而理應受到稱讚。
但是斷言達朗貝爾扭轉了乾坤,那是言過其實的。雖然他可能已經察覺到正確的路徑,但是他沒有在這條路徑上走得很遠。缺少的是「極限」的明確定義,以及沒有從極限出發推導微積分的一些基本定理。最終,達朗貝爾不過是提出了走出困境的方法而已。這些思想的完全確立尚需等待一代人或者更長的時間。
與此同時,一位更卓越的數學家捲入了這個難題,並且提出一種完全不同的解答。他就是約瑟夫·路易·拉格朗日(1736—1813)——18世紀晚期在歐洲數學界有著重大影響的一位傑出數學家。對於這個基礎性的問題,拉格朗日發誓要提供一個邏輯上完備的構架,使得微積分的宏偉大廈可以建立它的基礎上。在他1797年所寫的《解析函數論》一書中,他設想了一種「排除無窮小量、逐漸消失的量、極限以及流數所有因素在內」的微積分。12 鑒於以往的任何合理性都不具備優勢,拉格朗日宣誓要重新開始。
12 Joseph-Louis Lagrange, Oeuvres, vol. 9, Paris, 1813, p. 11(扉頁)。
他的基本思想是把無窮級數作為微分的源頭而不是結果。這就是說,拉格朗從他要尋找導數的函數f (x)開始,把 f (x+i)表示成 i 的無窮級數
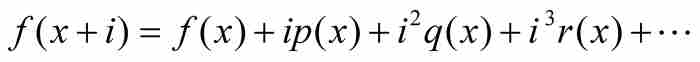 (1)
(1)
的形式,其中,正如他指出的那樣,「p,q,r,… 將是從簡單函數x導出的並且與i無關的新函數」。13 於是,f 的(一階)導數恰好就是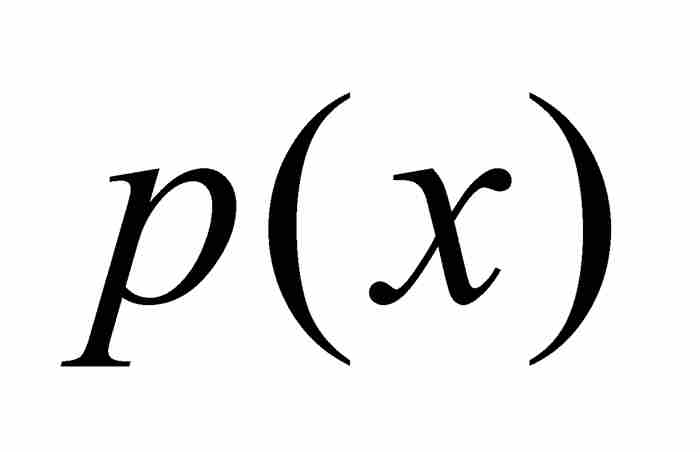 ,在這個展開式中,
,在這個展開式中,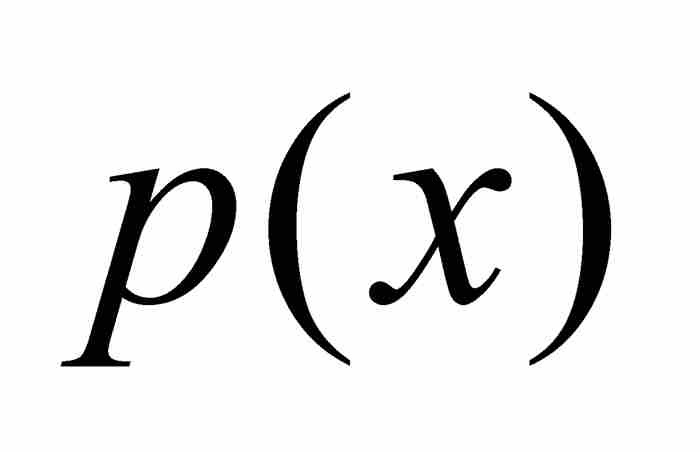 為i的係數。
為i的係數。
13 Joseph-Louis Lagrange, Oeuvres, vol. 9, Paris, 1813, pp. 21-22。
任何熟悉泰勒級數的人都會明白拉格朗日得到了什麼,但是對他而言重要的是注意這個級數出現在先,而導數是作為它的一個結果,在現代分析學中導數出現在級數之前。
用一個例子可以說明這一點。假定我們想求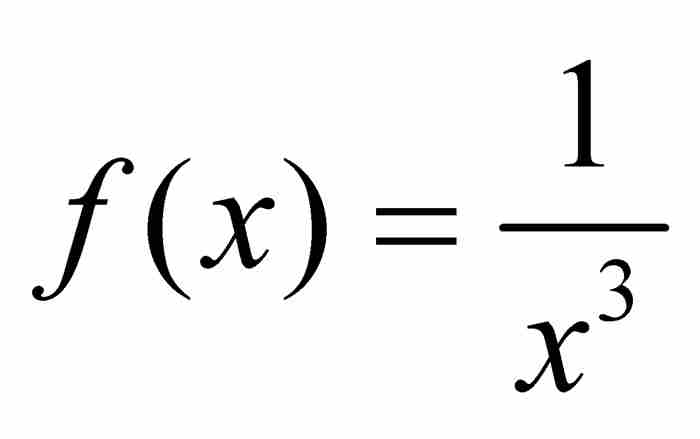 的導數
的導數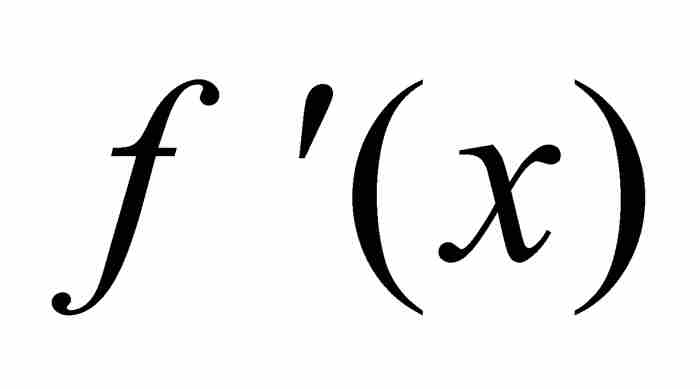 。(順便指出,「
。(順便指出,「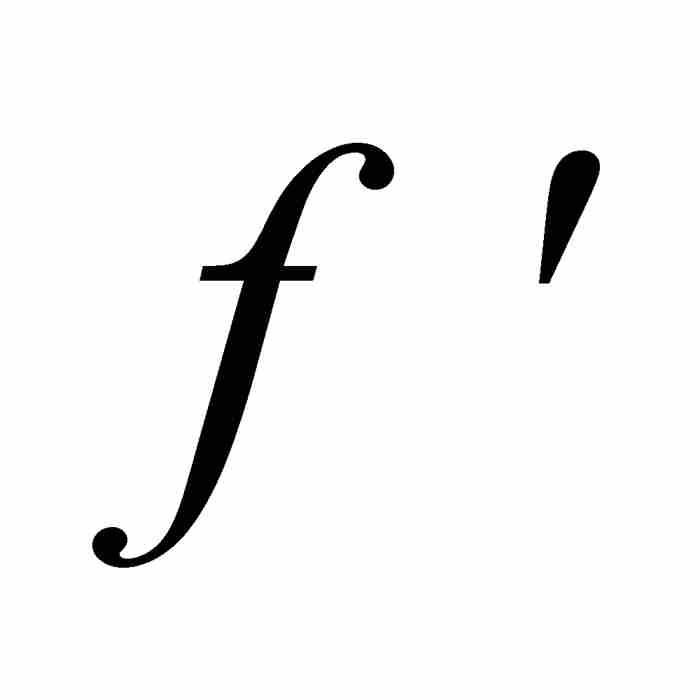 」這個記號來源於拉格朗日。)展開式(1)所示的函數,得到
」這個記號來源於拉格朗日。)展開式(1)所示的函數,得到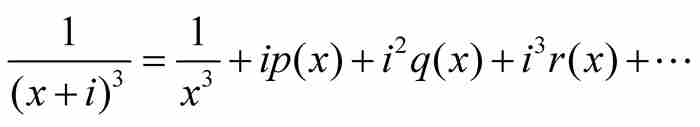 ,所以
,所以
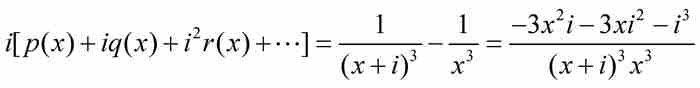
因此
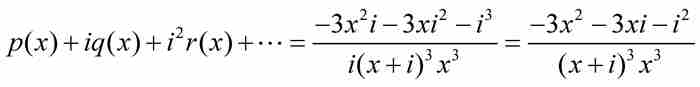 (2)
(2)
至此,拉格朗日在式(2)中令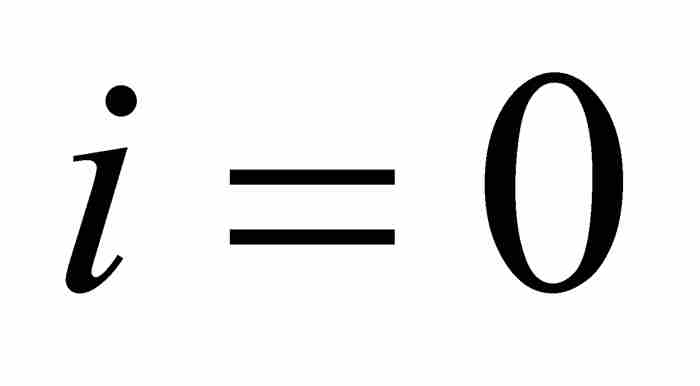 ,得到
,得到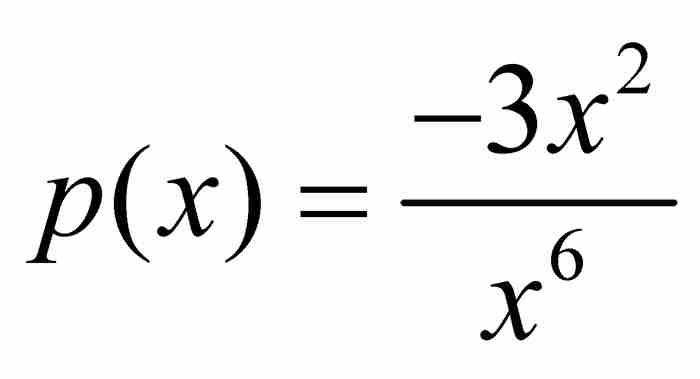 。因此,
。因此,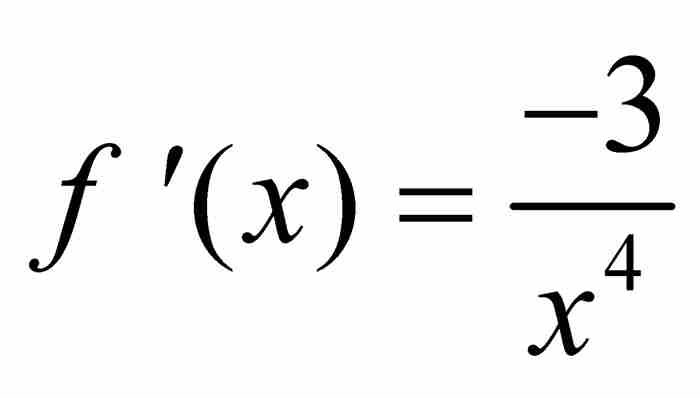 。對牛頓或萊布尼茨來說,這個結果自然是不足為奇的。
。對牛頓或萊布尼茨來說,這個結果自然是不足為奇的。
對拉格朗日而言,這個推導過程避免了無窮小量,同時也避免了那些湮滅不見的消逝的量的鬼魂。同樣,他無需用達朗貝爾的沒有確切定義的極限。當拉格朗日令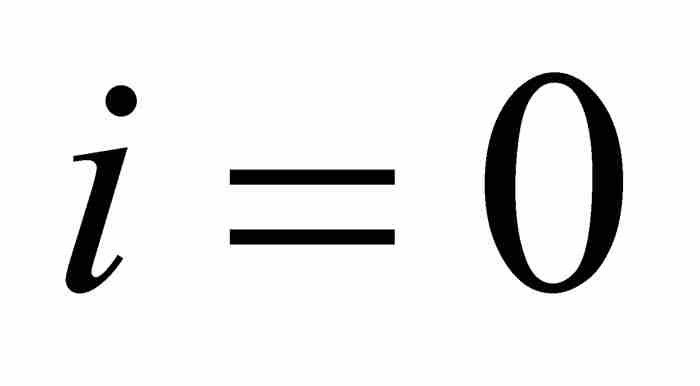 時,他的意思是嚴格的。在式(2)中不會遇到任何陷阱,因為在任何分母中都沒有出現零。他認為這是解決導數問題的純粹的分析方法,不需要任何曾經困擾他的先驅們的邏輯轉換。這個方法竟然如此精緻,如此整齊。
時,他的意思是嚴格的。在式(2)中不會遇到任何陷阱,因為在任何分母中都沒有出現零。他認為這是解決導數問題的純粹的分析方法,不需要任何曾經困擾他的先驅們的邏輯轉換。這個方法竟然如此精緻,如此整齊。
然而,果真是這樣嗎?舉一個事例,可以說明用這種方式定義導數過於曲折。儘管牛頓和萊布尼茨的思想夾雜著曲線和三角形,並且建立在不牢固的基礎之上,但是他們對研究對象的定義是直接的。在拉格朗日的思想中沒有任何的圖解,卻把導數同切線斜率有關的事實完全掩蓋了。
這還只是次要的毛病。更大的麻煩是在對待比上述函數更為複雜的函數如何求導數的問題上。在我們的例子中,問題的關鍵是展開並且簡化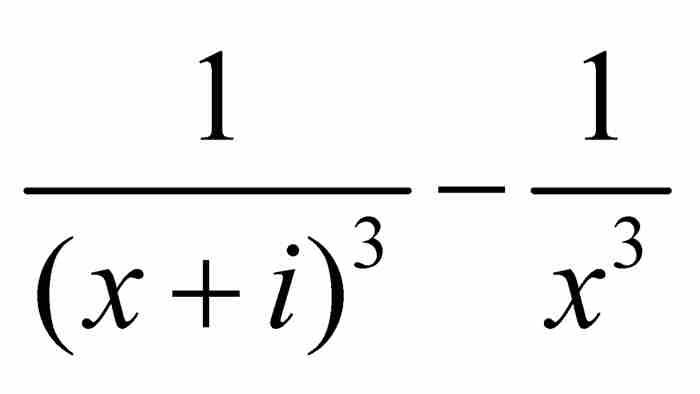 ,以便從結果中分解出因子i。但是每個函數的可以展開和簡化的保證在哪裡?這樣構造的級數是收斂的保證在哪裡?而這樣構造的一個收斂級數收斂到我們原始的函數的保證又在哪裡?這些才是深層次的和重要的問題。
,以便從結果中分解出因子i。但是每個函數的可以展開和簡化的保證在哪裡?這樣構造的級數是收斂的保證在哪裡?而這樣構造的一個收斂級數收斂到我們原始的函數的保證又在哪裡?這些才是深層次的和重要的問題。
最終,拉格朗日的理論經不起如此嚴格的推敲。1822年,法國數學家奧古斯丁·路易·柯西發表了一個例子,證實拉格朗日的思想存在致命缺陷。我們在下一章的主角柯西證明了函數
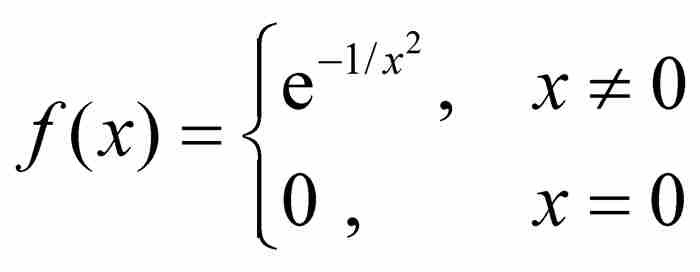
及其在x=0的各階導數為零。14 因此,作為原來函數的冪級數,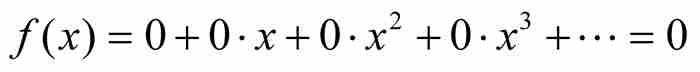 。這反過來說明,如果我們從函數 f 開始,將它寫成級數的形式,我們得到一個完全不同於開初的函數!作為一個級數,我們無法區分上面的函數 f 和常值函數
。這反過來說明,如果我們從函數 f 開始,將它寫成級數的形式,我們得到一個完全不同於開初的函數!作為一個級數,我們無法區分上面的函數 f 和常值函數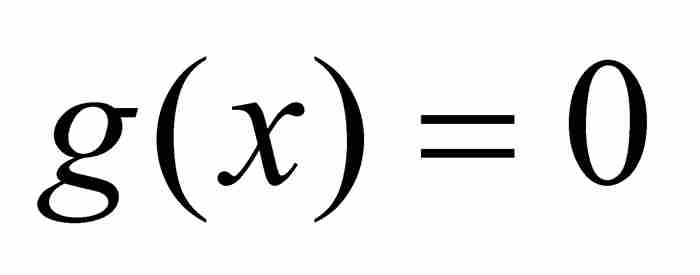 。柯西的兩個不同的函數有一個共同冪級數的例子,說明分析學完全不能按照拉格朗日的設想來創建。
。柯西的兩個不同的函數有一個共同冪級數的例子,說明分析學完全不能按照拉格朗日的設想來創建。
14 Augustin-Louis Cauchy, Oeuvres, ser. 2, vol. 2, Paris, pp. 276-278。
總之,基於級數的導數定義以及隨之而來的基於級數的微積分的基礎被拋棄了。雖然拉格朗日未能完成他的主要使命,但卻作出了許多貢獻,引導了新世紀的發展。首先,他將基礎問題提升到更突出的位置,使之成為既有趣又重要的問題。其次,他試圖從他的基本定義推導出微積分的種種定理,在這個過程中引入了不等式,並且對不等式的應用展現出熟練的技巧。最後,正如Judith Grabiner在她的《柯西的嚴密微積分的起源》一書中所說:
閱讀拉格朗日的著作,人們總是會被他對普遍性的感悟所打動……,他對普遍性的極端鍾情在那個年代是非同尋常的,與許多他同時代人專注於解決特定問題形成鮮明對比。他提出的微積分的代數基礎與其普遍化的思想傾向是一致的。15
15 Judith Grabiner, The Origins of Cauchy\'s Rigorous Calculus, MIT Press, 1981, p. 30。
儘管數學家們作出了這麼多貢獻,在18世紀結束時,微積分的邏輯危機依然沒有解決。達朗貝爾和拉格朗日以及其他致力於處理這些問題的數學家的工作沒能平息批評的浪潮。伯克萊主教說過這麼一句話:「我要指出在其他每一種科學中,人們總是用他們的原理來證明結論,而不是用他們的結論來證明原理。」直到進入19世紀,他的話聽起來還一直帶有真實性的意味。16
16 George Berkeley, The Works of George Berkeley, vol. 4, Neison & Sons, London, 1951, p. 76。
但是一種解決方案近在咫尺了。在19世紀初期,正是認識到級數非唯一性的柯西,行將發現一個可以圓滿解釋微積分基礎的方法。到他完成這個任務的時候,分析學就超越了他的前輩們所能設想的情景,成為遠具普遍性、抽像性和充滿不等式的學科。同時,這門學科將會越發嚴密。
現在我們就轉向這位傑出的人物,轉向他所進行的革命性的工作。
