
艾薩克·牛頓(1642—1727)
艾薩克·牛頓不但是數學上的開創性人物,而且是整個西方思想史上舉足輕重的人物。當他出生時,科學尚未確立對中世紀迷信至高無上的統治地位,而在他去世時,理性時代已經步入全盛時期。這一不同尋常的轉變在一定程度上應歸功於他的貢獻。
作為數學家,牛頓被推崇為微積分或者他為之命名的「流數術」的創立者。微積分的起源要追溯到17世紀60年代中期,那時牛頓還是劍橋大學三一學院的一名學生。在那裡牛頓專心研究勒內·笛卡兒(1596—1650)、約翰·沃利斯(1616—1703)以及三一學院第一位盧卡斯數學教授艾薩克·巴羅(1630—1677)這樣一些先驅們的著作,但是很快他就發現自己進入了一個從未有人涉足的領域。在接下來的幾年中,牛頓永遠地改變了數學的面貌,傳記作家Richard Westfall把他這幾年描繪為一個「光芒四射的活動」時期。1 到1669年,巴羅本人將他的這位繼任者和同事形容為「我們學院的一位同伴,非常年輕……,但卻是一位具有非凡天賦和卓越才能的人物」。2
1 Richard S. Westfall, Never at Rest, Cambridge University Press, 1980, p. 134。
2 Richard S. Westfall, Never at Rest, Cambridge University Press, 1980, p. 202。
在本章,我們來考察一下牛頓早期的如下幾個成就:將某些表達式轉換為無窮級數的廣義二項展開式,求無窮級數的逆級數的方法,以及確定曲線之下的面積的求積法則。最後我們介紹一個驚人的結果,即一個角的正弦的級數展開。關於二項展開式的最早描述出現在他回答萊布尼茨詢問的《前信》3中,那是在他完成最初的研究工作很久以後。本章其他素材來自牛頓1669年的論著《運用無窮多項方程的分析學》,這本著作通常簡稱為《分析學》。
3 為答覆萊布尼茨的有關詢問,牛頓在1676年先後兩次致信英國皇家學會秘書H.奧爾登堡,分別稱為《前信》和《後信》,在《前信》中追述了對二項式定理的原始推導和思路。——譯者注
儘管本章僅限於討論牛頓早期的工作,但是需要指出,牛頓「早期的工作」幾乎總是超越其他任何人深思熟慮的工作。
廣義二項展開式
截至1665年,牛頓已經發現將二項式展開(他的說法是「化簡」)成級數的簡單方法。對他而言,這種化簡不僅是用另一種形式重建二項式的手段,同時也是通向流數術的大門。這個二項式定理是牛頓眾多數學發明的起點。
正如《前信》所述,眼前的問題是化簡二項式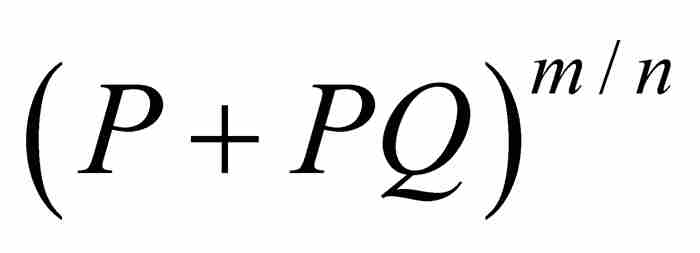 ,而不管m/n「是整數還是分數,或者是正數還是負數」。1 在人們對指數還非常生疏的時代,這本身是一個非常大膽的思想,那時牛頓首次強調「用
,而不管m/n「是整數還是分數,或者是正數還是負數」。1 在人們對指數還非常生疏的時代,這本身是一個非常大膽的思想,那時牛頓首次強調「用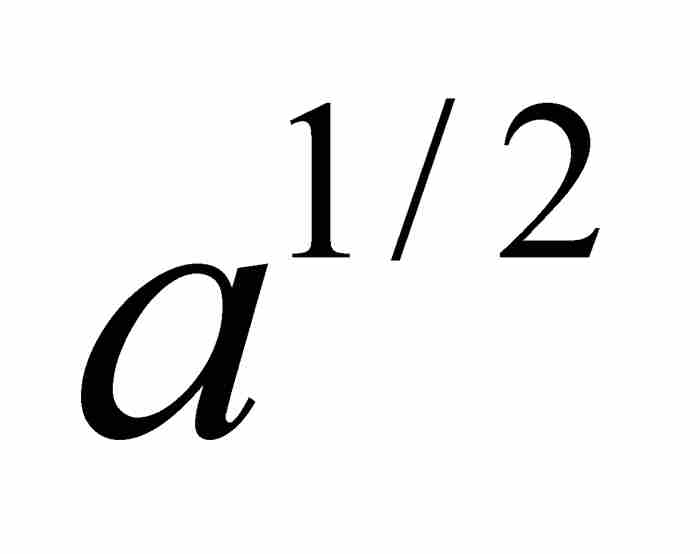 ,
,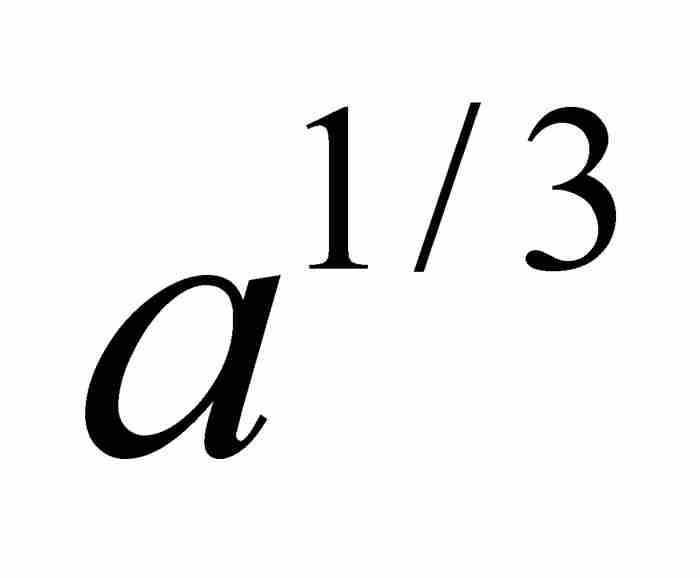 ,
,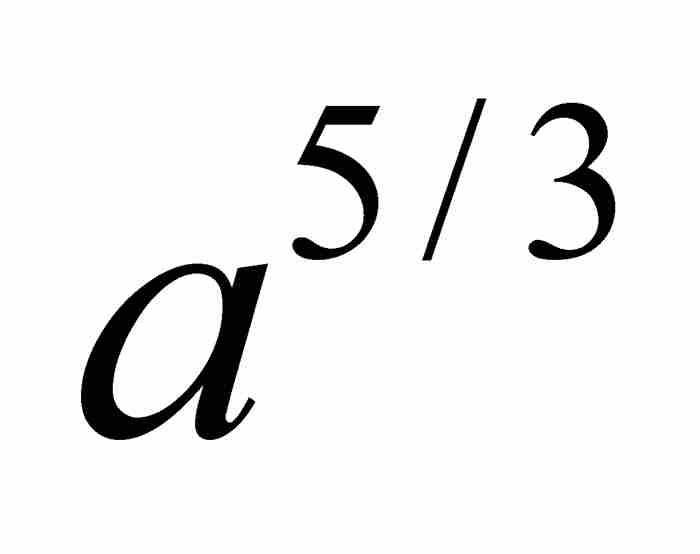 代替
代替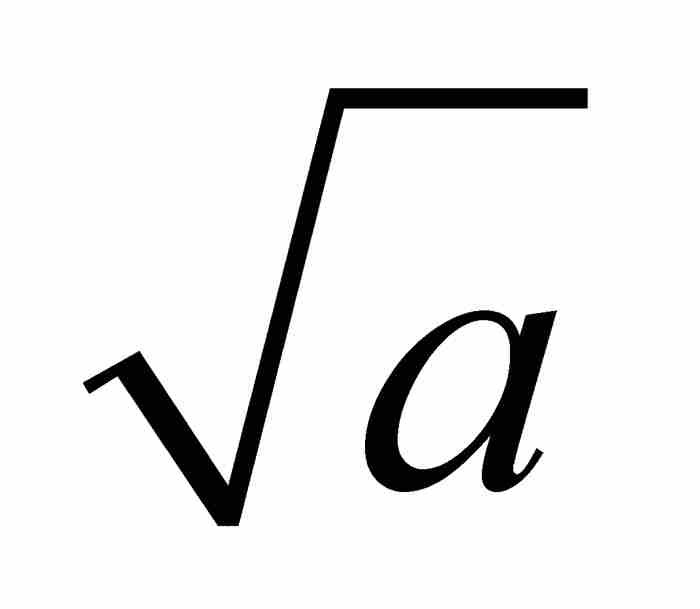 ,
,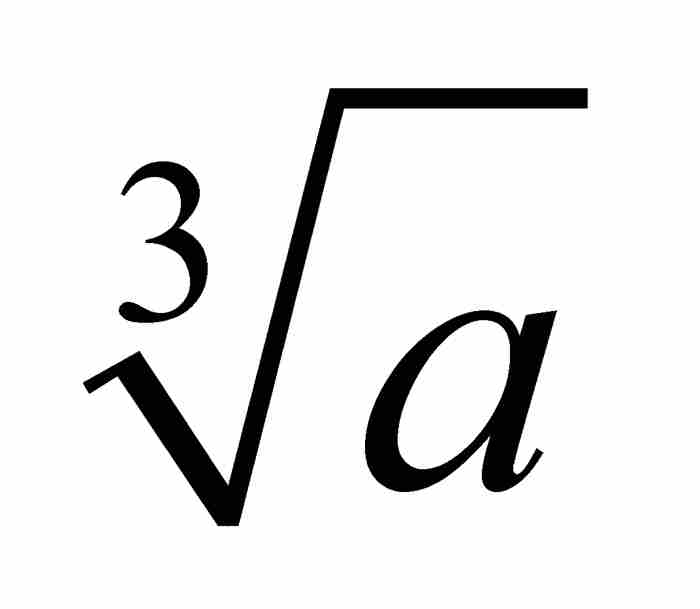 ,
,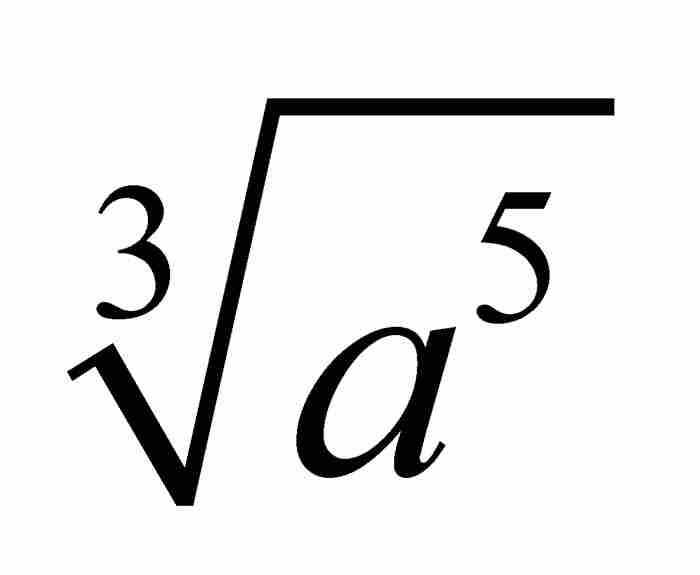 , 用
, 用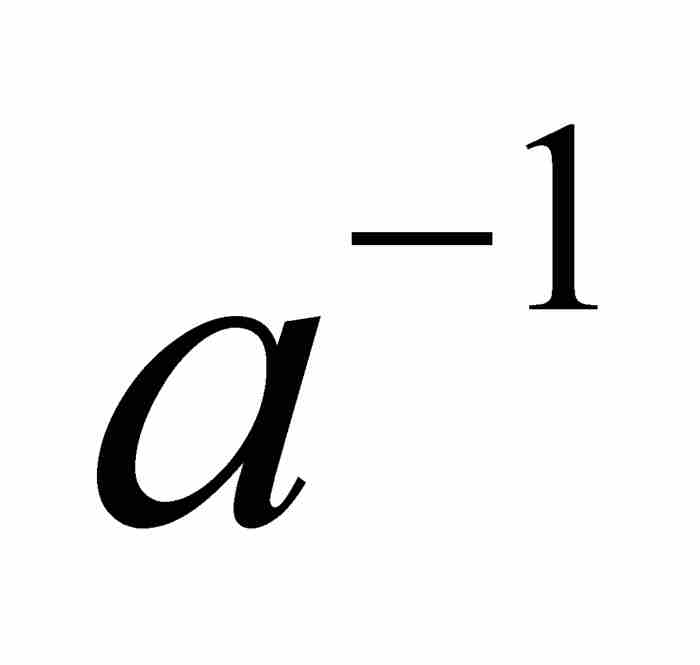 ,
,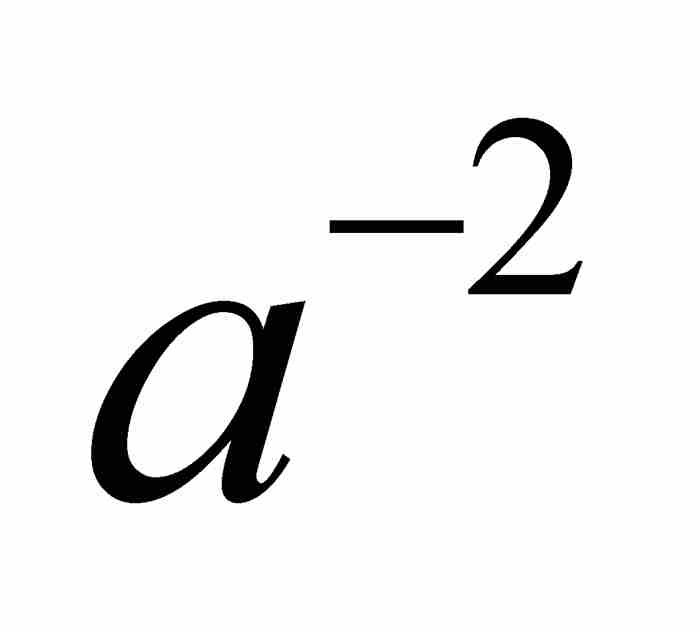 ,
,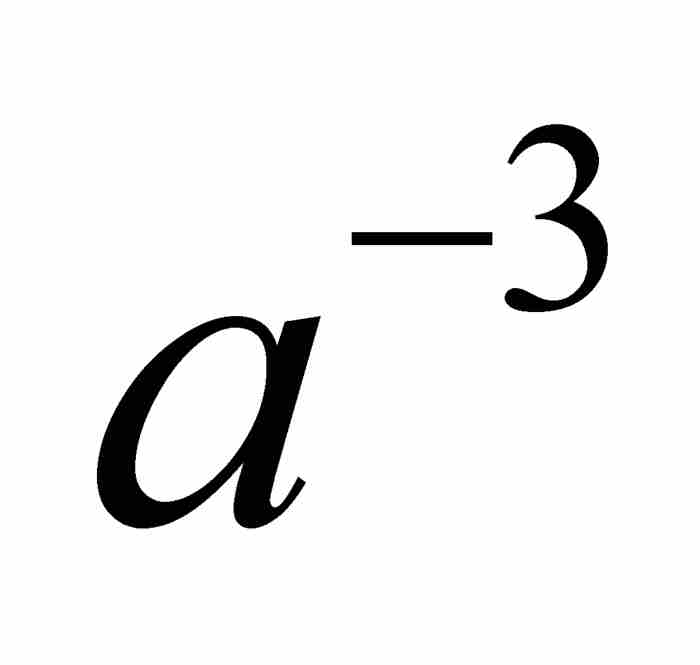 代替
代替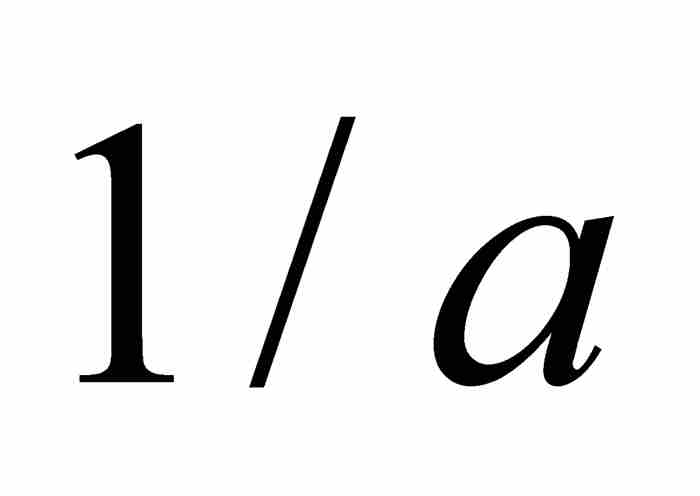 ,
,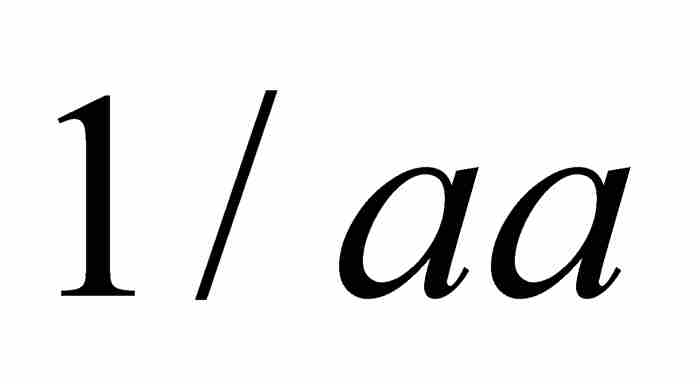 ,
,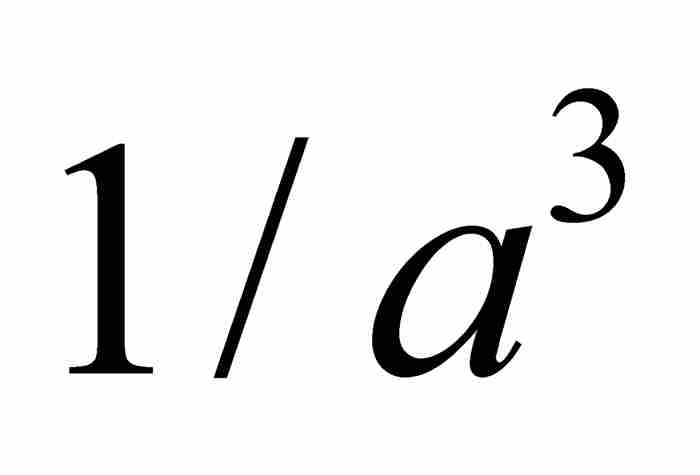 」。2 顯然,當時的讀者需要適當的提示。
」。2 顯然,當時的讀者需要適當的提示。
1 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard Vniversity Press, 1969, p. 286。
2 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard Vniversity Press, 1969, p. 286。
牛頓不但發現了像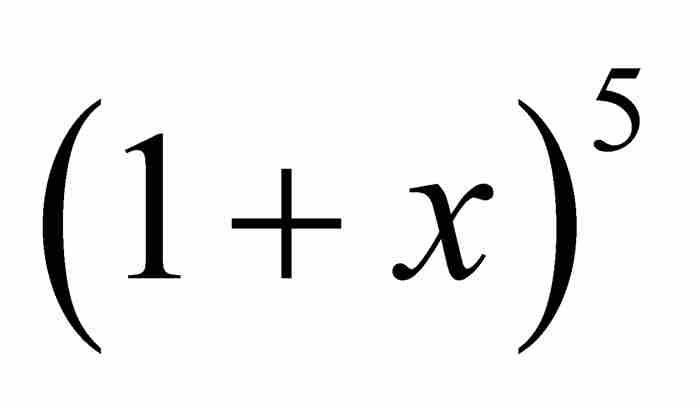 這樣基本的二項式的展開形式,而且發現了像
這樣基本的二項式的展開形式,而且發現了像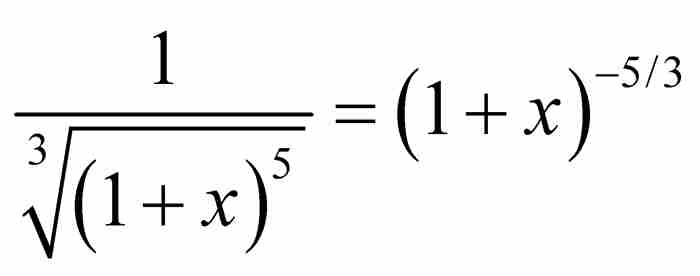 這樣複雜的二項式的展開形式。正如牛頓向萊布尼茨解釋的那樣,這種化簡服從規則
這樣複雜的二項式的展開形式。正如牛頓向萊布尼茨解釋的那樣,這種化簡服從規則
 (1)
(1)
其中A,B,C, …分別代表前一項,我們將在下面舉例說明。這就是著名的牛頓二項式展開式,雖然這種形式或許是新奇的。
牛頓給出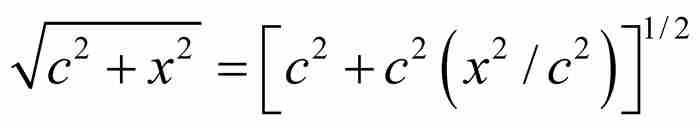 的例子。在這個例子中
的例子。在這個例子中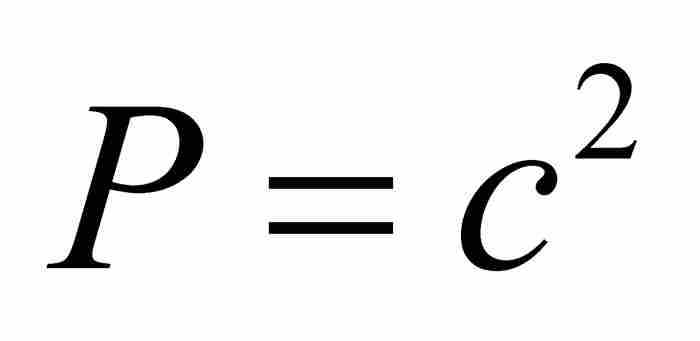 ,
,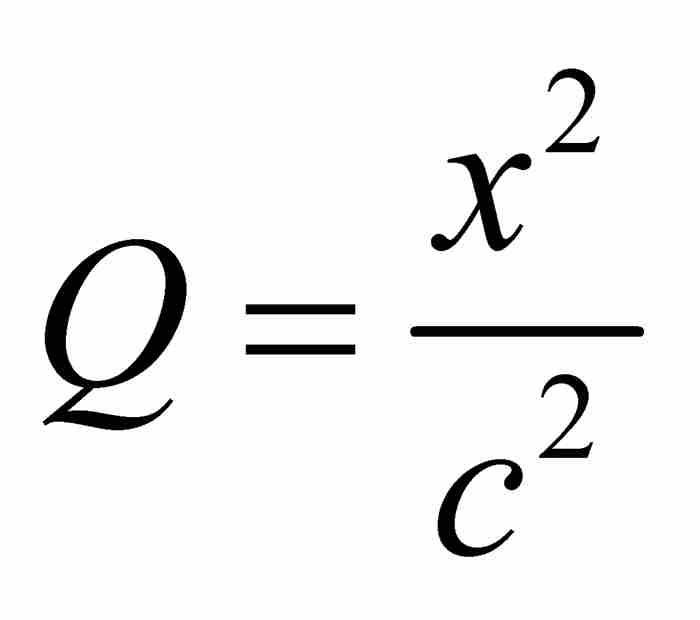 ,
,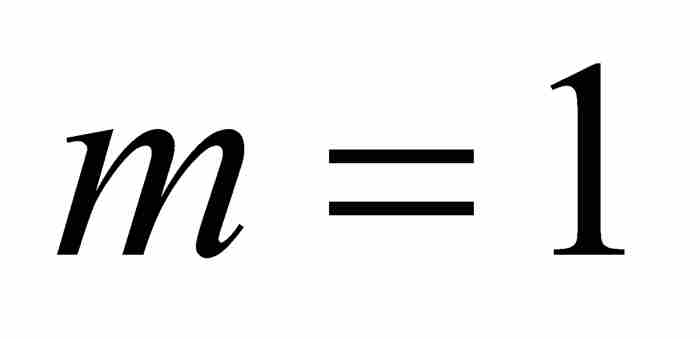 ,
,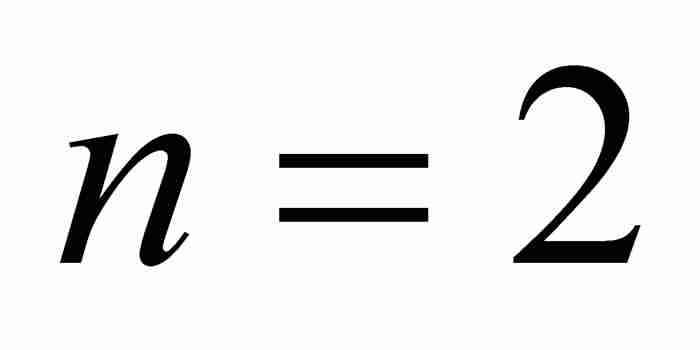 。因此,
。因此,
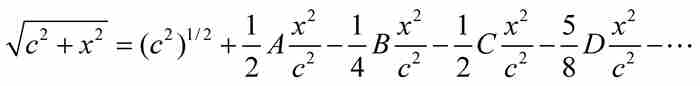
為了確定A, B, C及其他係數,我們可以利用它們都表示前一項的事實。於是,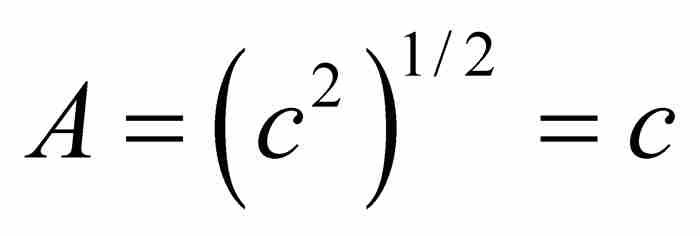 ,給出
,給出
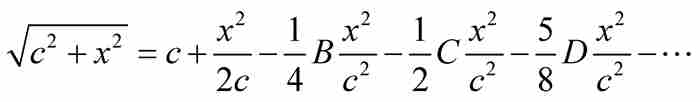
同樣,B表示前一項,即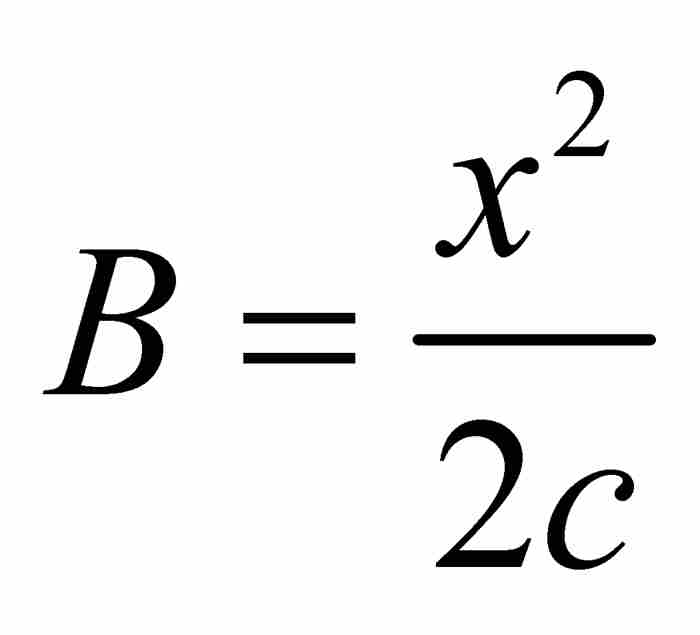 ,由此得到
,由此得到
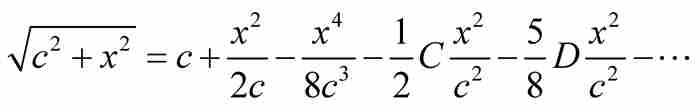
用類似的代入得到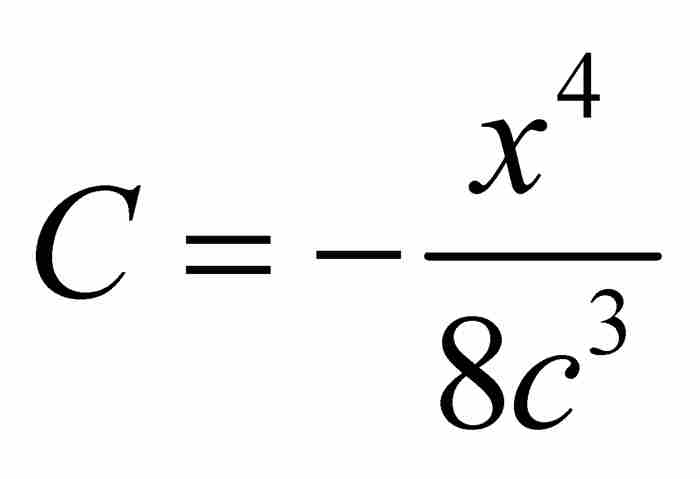 ,然後得到
,然後得到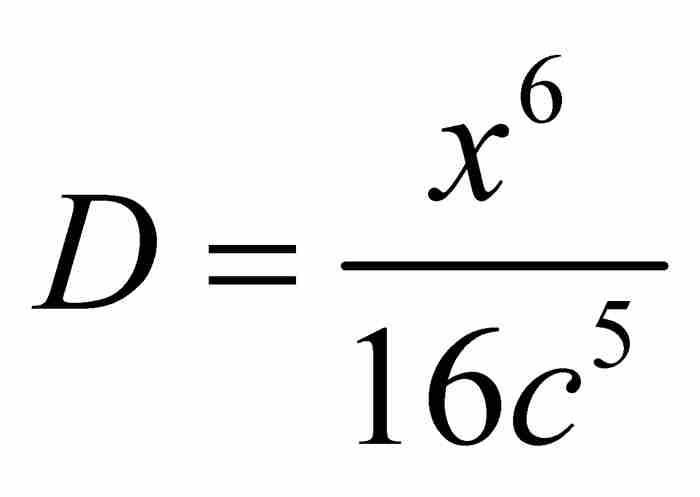 。以這種方式從左到右繼續推導,牛頓得到
。以這種方式從左到右繼續推導,牛頓得到
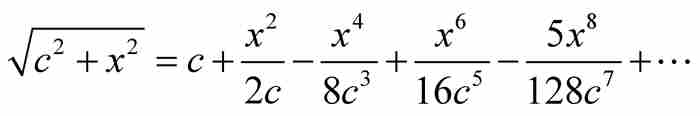
顯然,這種方法有一點遞歸的味道:從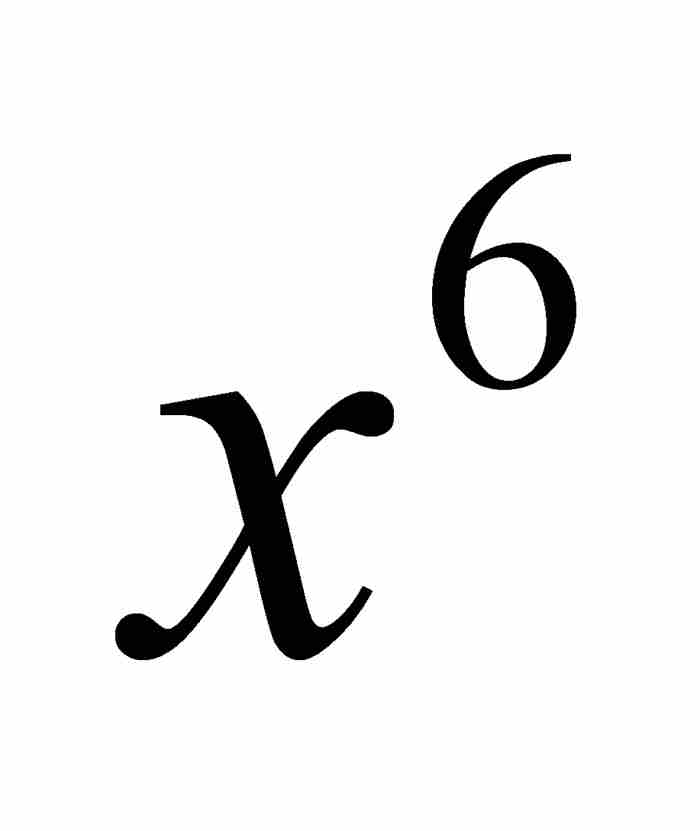 的係數求出
的係數求出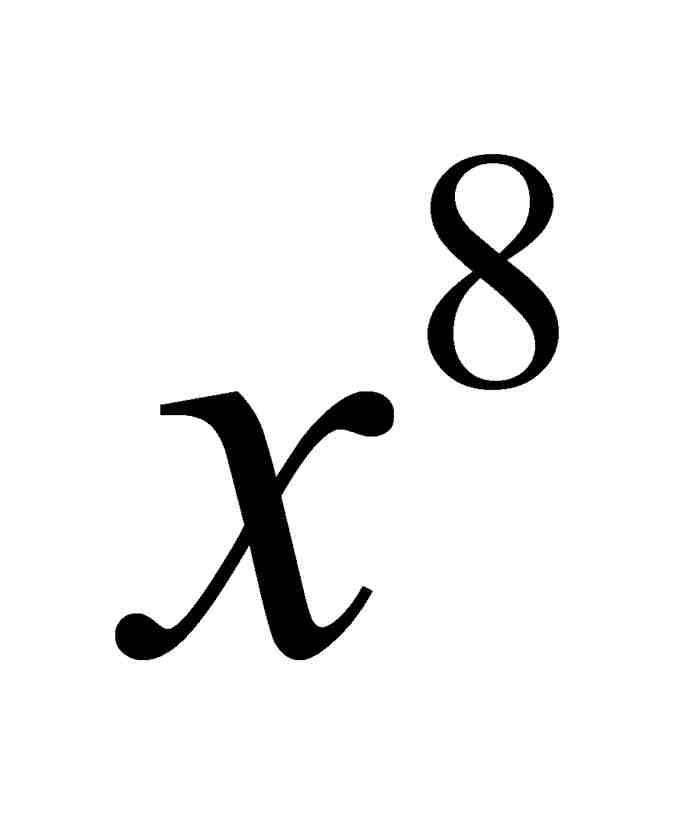 的係數,而欲求
的係數,而欲求 的係數需要知道
的係數需要知道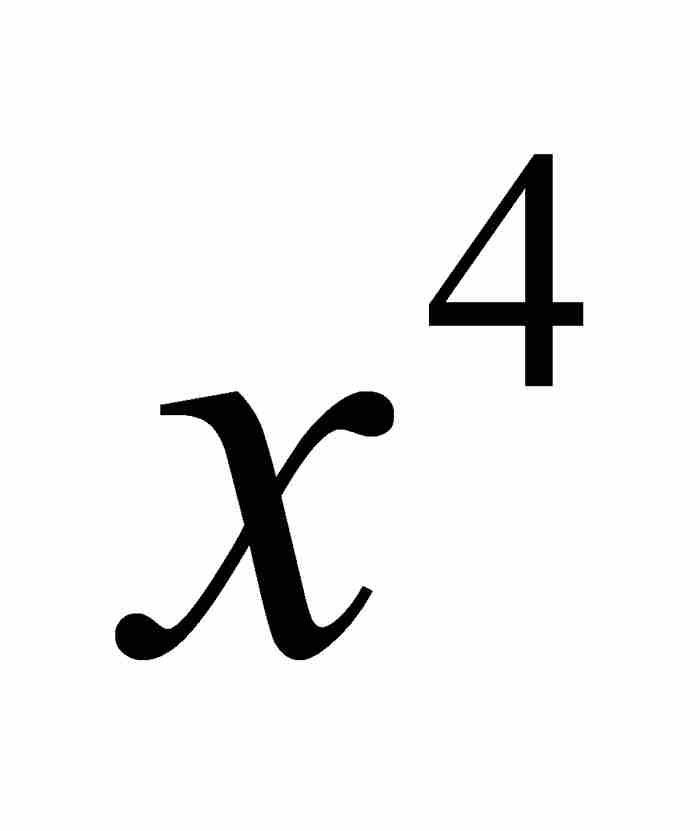 的係數,依此類推。雖然現代的讀者可能習慣於二項式定理的直接表述,但是牛頓的遞歸表示具有無可爭辯的吸引力,因為當用前一項來計算後一項的數值係數時,可以使計算過程得以簡化。
的係數,依此類推。雖然現代的讀者可能習慣於二項式定理的直接表述,但是牛頓的遞歸表示具有無可爭辯的吸引力,因為當用前一項來計算後一項的數值係數時,可以使計算過程得以簡化。
為明確起見,簡單的方法是用由P和Q表示的A, B, C, …的等價表達式代替A, B, C, …,然後約去式(1)兩端的公因子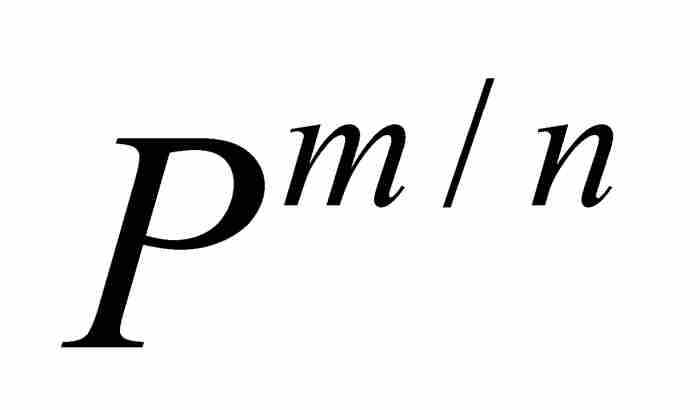 ,就獲得現在的公式:
,就獲得現在的公式:
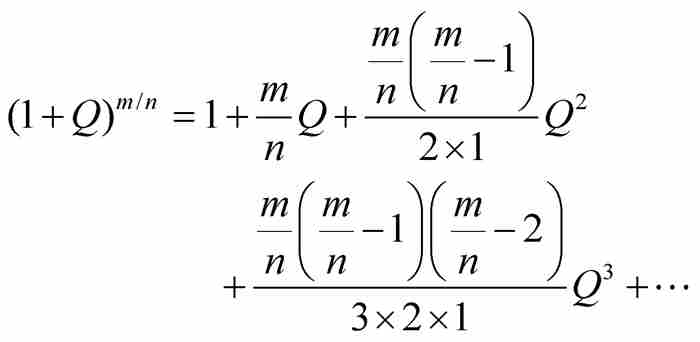
(2)
牛頓將這種簡化比作是從平方根到無窮小數的轉換,並且不遺餘力地推崇這一運算的好處。他在1671年寫道:
這是一種產生無窮級數的簡便方法,所有複雜的項……都可以簡化為一類簡單的量,即分子和分母都是簡單項的分數的無窮級數,這樣將會消除那些其原始形式看起來幾乎難以逾越的困難。3
3 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 37。
的確,將數學家從不可逾越的難題中解脫出來是一件值得做的事情。
再舉一個有助於理解的例子——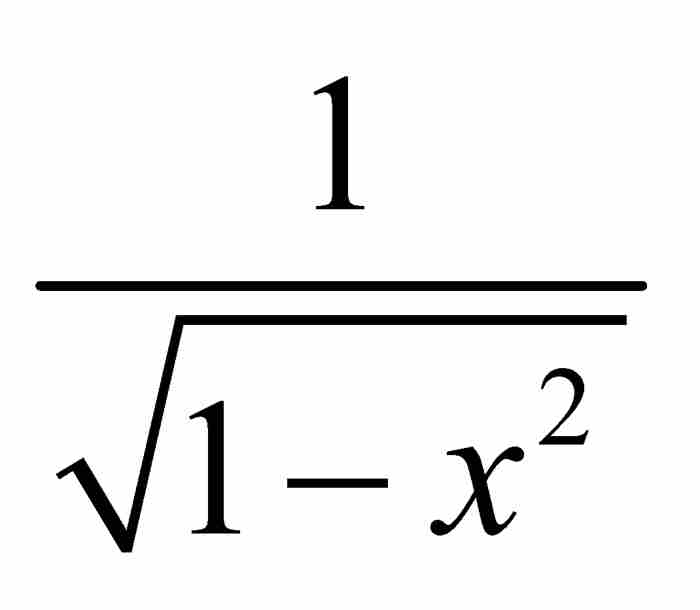 的展開式,在本章後面將要討論的一個結果中,將會展示牛頓對這個展開式的巧妙應用。我們首先將上式寫成
的展開式,在本章後面將要討論的一個結果中,將會展示牛頓對這個展開式的巧妙應用。我們首先將上式寫成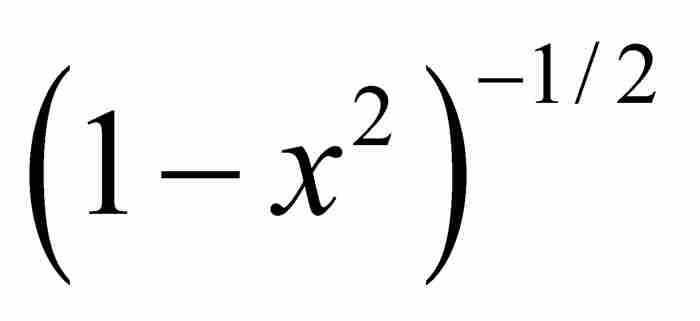 ,確定
,確定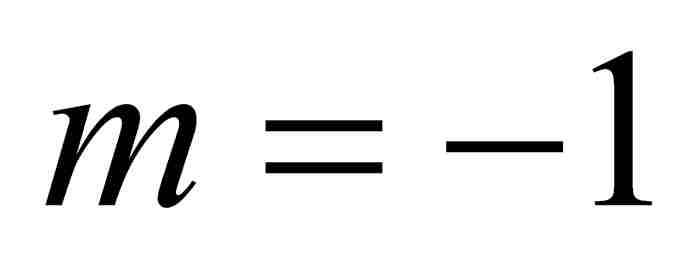 ,
,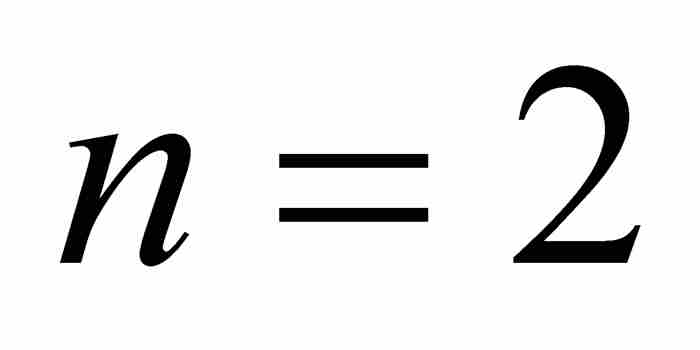 ,
,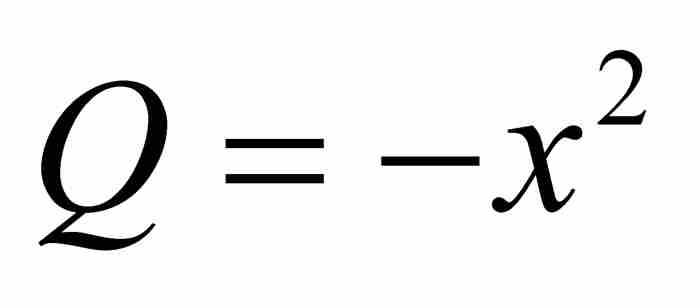 ,並利用式(2):
,並利用式(2):

(3)
牛頓通過將級數平方並檢查其結果來「檢驗」式(3)這樣的展開式。如果我們也這樣做,並且限制取次數不超過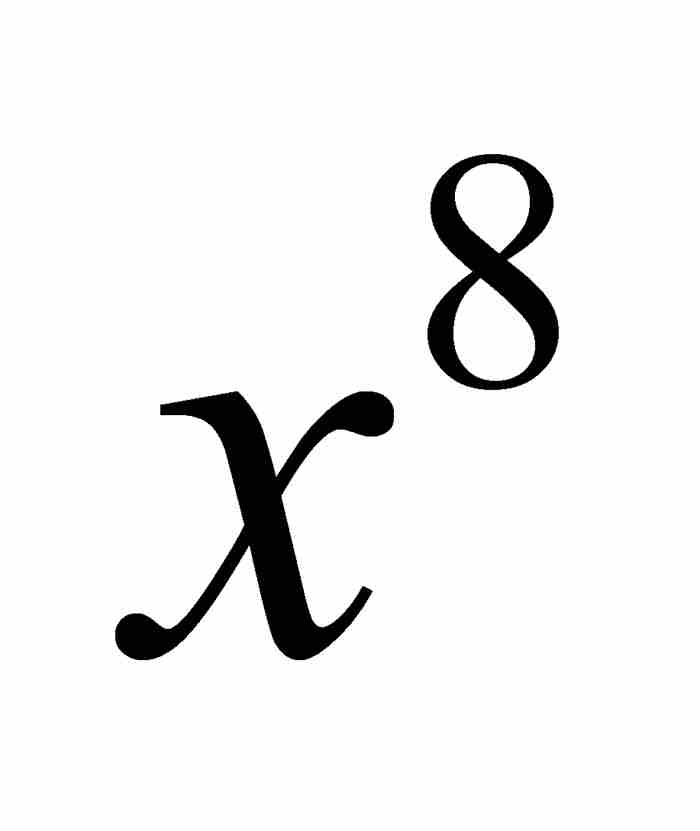 的項,得到
的項,得到
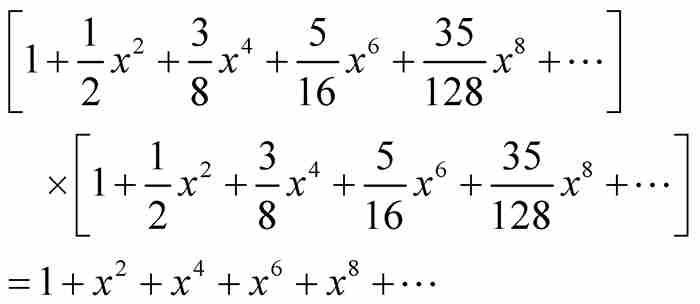
其中全部係數奇跡般地變成了1(讀者不妨試試吧!)。自然,得到的乘積是公比為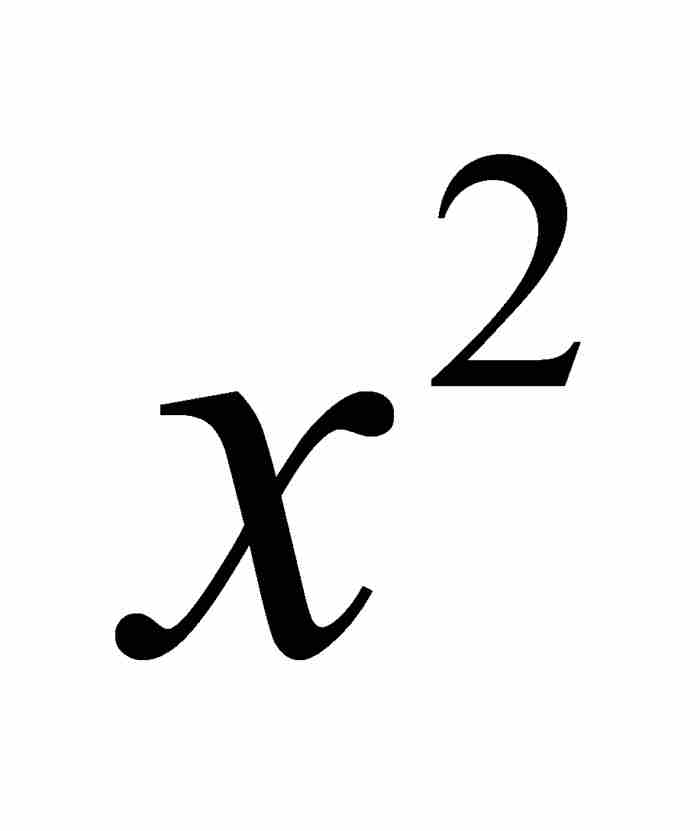 的無窮等比級數,由已有的公式可知,其和為
的無窮等比級數,由已有的公式可知,其和為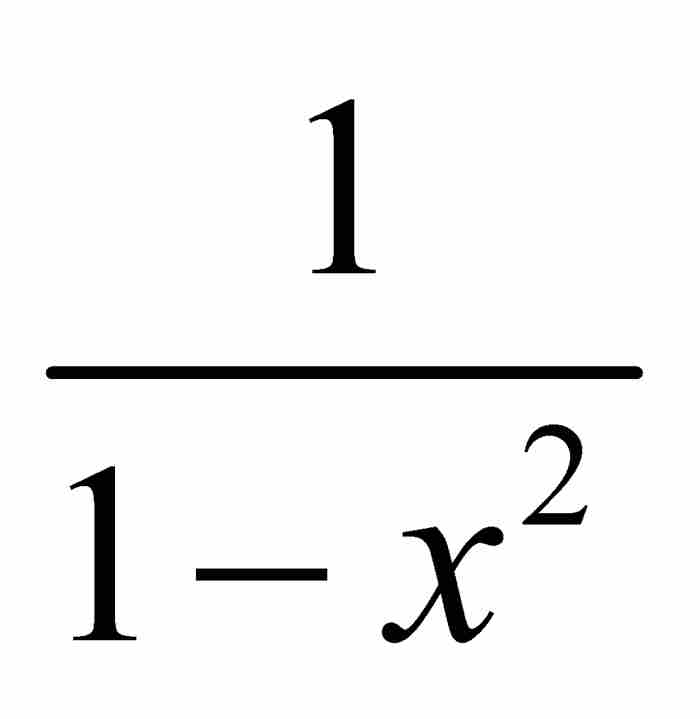 。但是,如果級數(3)的平方為
。但是,如果級數(3)的平方為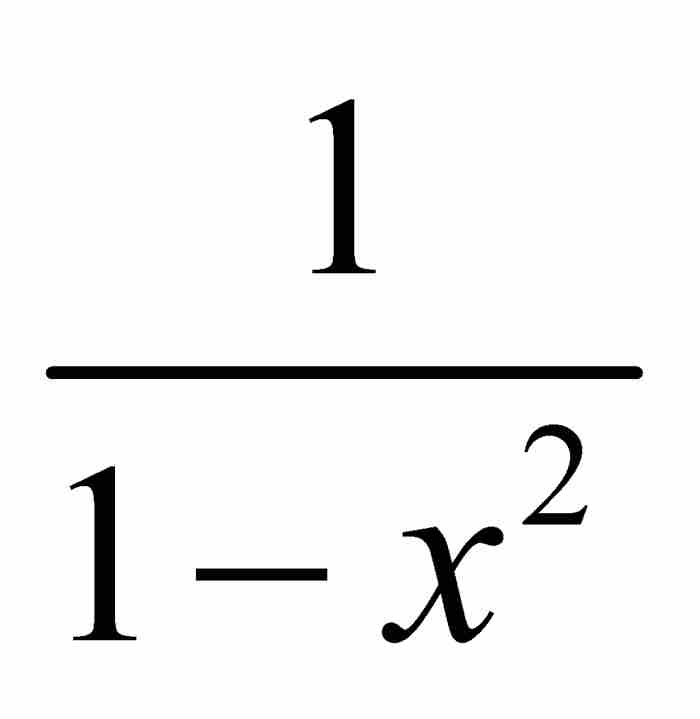 ,那麼,我們推斷級數本身必定是
,那麼,我們推斷級數本身必定是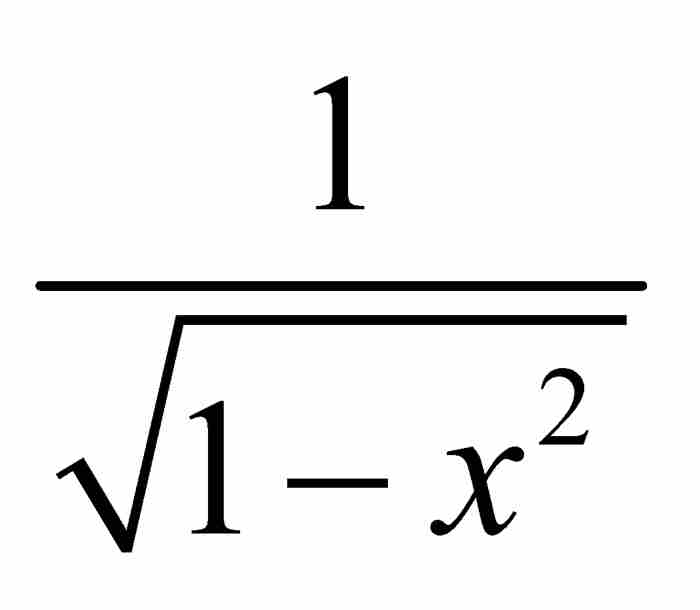 。妙極了!
。妙極了!
牛頓將這樣的計算當作讓人信服他的普遍性結論的證明。他斷言「儘管我們這些凡人的推理能力非常有限,既不能表達也不能想像這些等式的所有項,就像我們無法確切知道那些量從何而來一樣」,但是「可以把對有限項等式的一般分析」推廣到這樣的無限項表達式。4
4 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 22。
逆級數
在描述把某些二項式化簡為形如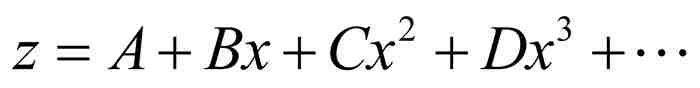 的無窮級數的方法以後,牛頓進一步尋找通過z的項把x表示成級數的方法。用現在的術語,他是尋找逆級數關係。所得到的方法對代數學並未產生顯著影響,但是隨後將會看到,我們對它的關注是正確的。像牛頓的做法一樣,我們通過一個特例來描述求逆級數的過程。
的無窮級數的方法以後,牛頓進一步尋找通過z的項把x表示成級數的方法。用現在的術語,他是尋找逆級數關係。所得到的方法對代數學並未產生顯著影響,但是隨後將會看到,我們對它的關注是正確的。像牛頓的做法一樣,我們通過一個特例來描述求逆級數的過程。
讓我們從級數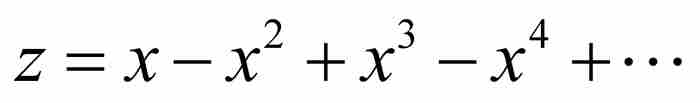 開始,首先將它改寫為
開始,首先將它改寫為
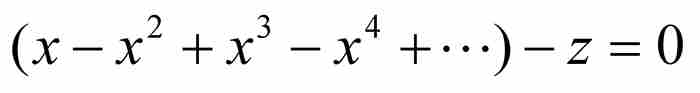 (4)
(4)
並且捨棄所有x的指數大於或等於2的項。自然,這樣剩下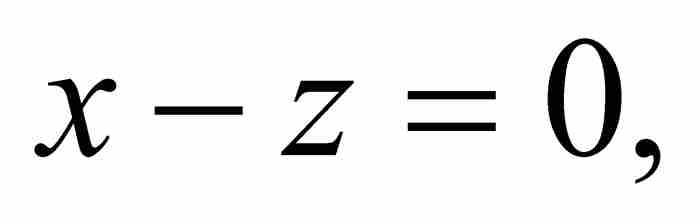 ,從而,逆級數開始於
,從而,逆級數開始於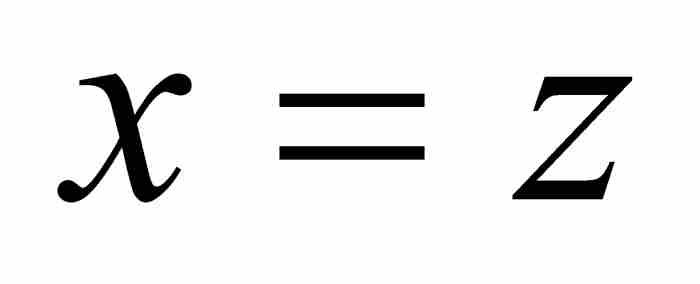 。
。
牛頓認識到捨棄全部高階項會導致不準確的解。準確的答案應該具備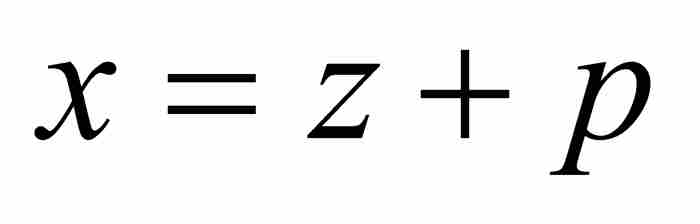 的形式,其中p是有待確定的級數。在式(4)中,用
的形式,其中p是有待確定的級數。在式(4)中,用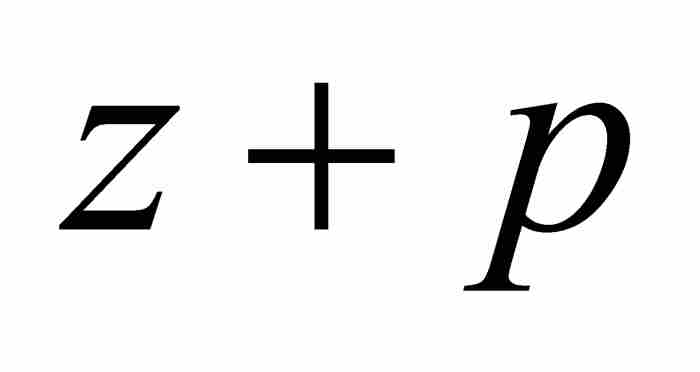 代換x,得到
代換x,得到
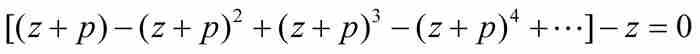
將上式展開並整理後,得到
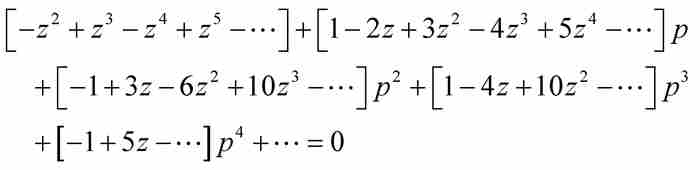 (5)
(5)
下一步,捨棄p的2次方項、3次方項和更高次方項,再求解,得到
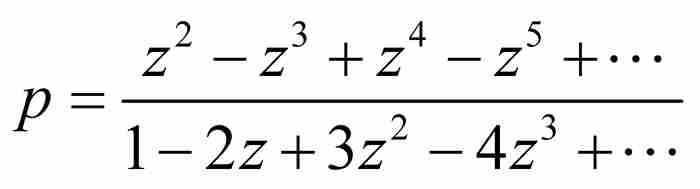
現在,牛頓實施第二輪刪除,捨棄分子和分母中除去z的最低次方項以外的所有z的高次方項。由此,p近似等於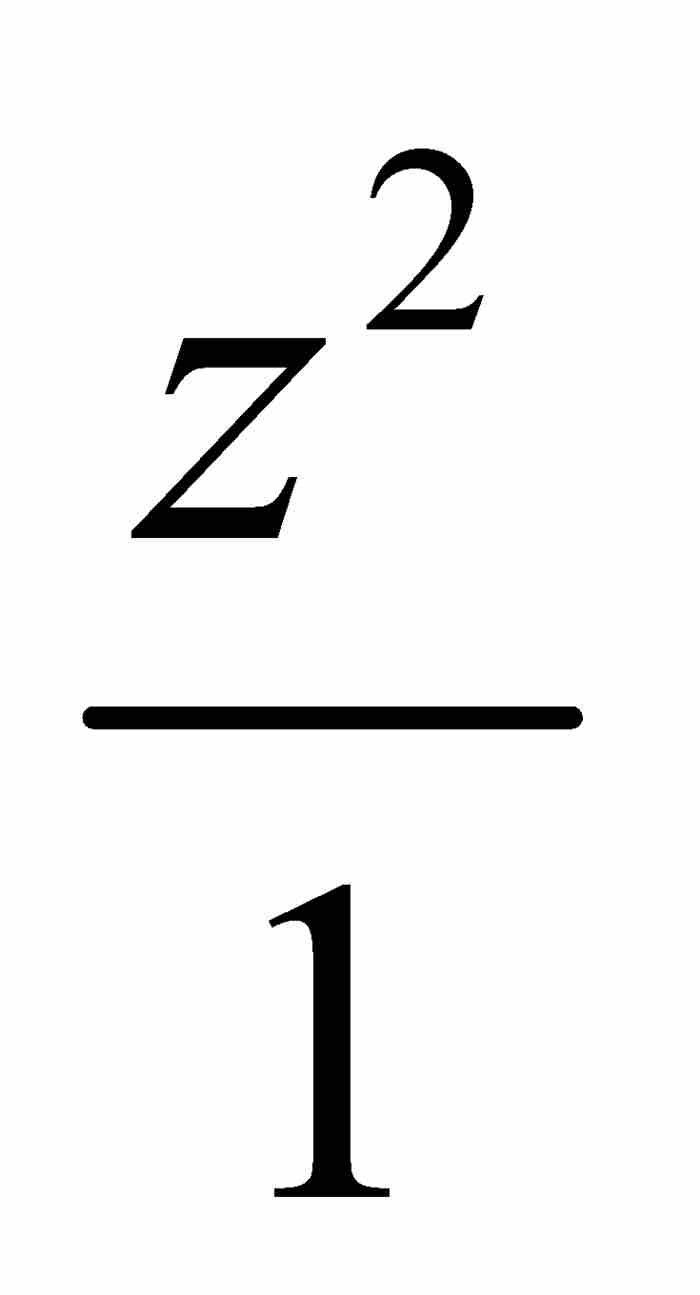 ,所以,到這一步逆級數表示為
,所以,到這一步逆級數表示為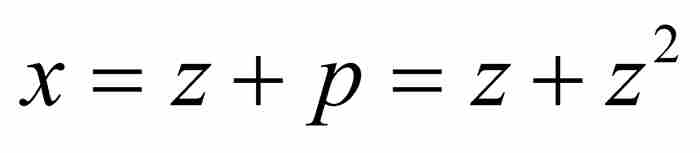 。
。
但是p並非恰好等於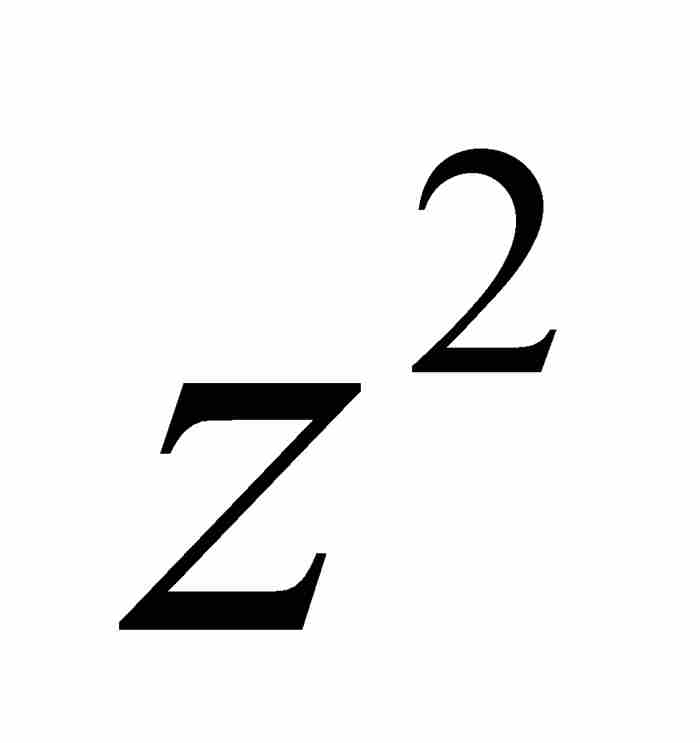 。更準確地說,
。更準確地說,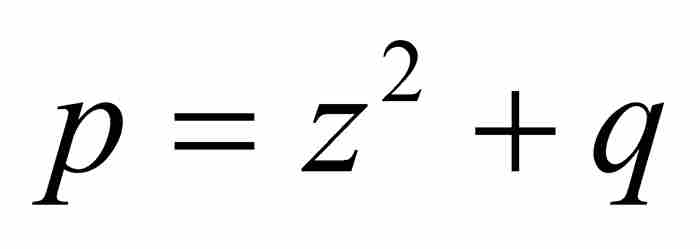 ,其中q是有待確定的級數。為求出q,我們將其代入式(5),得到
,其中q是有待確定的級數。為求出q,我們將其代入式(5),得到
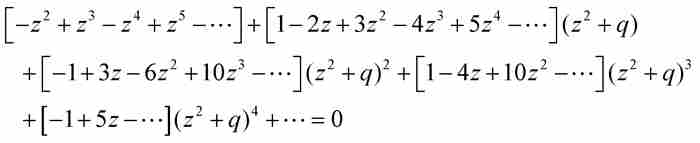
展開並按q的乘方合併同類項,得到
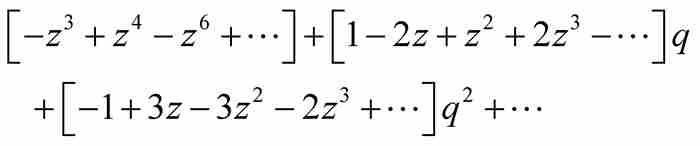 (6)
(6)
同前面一樣,捨棄q的高於1次方的項,求解得到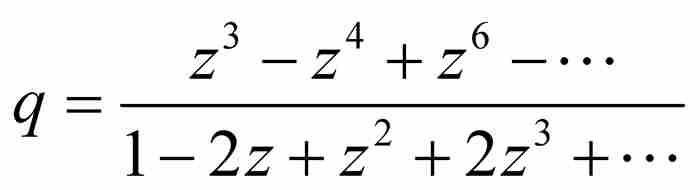 ,然後捨棄分子分母中除去z的最低次方項以外的所有項,得到
,然後捨棄分子分母中除去z的最低次方項以外的所有項,得到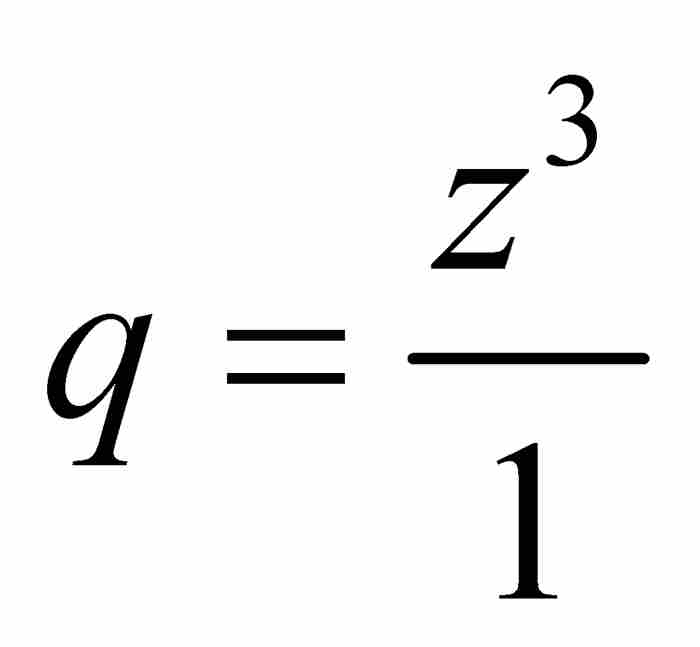 。至此,級數的形式變成了
。至此,級數的形式變成了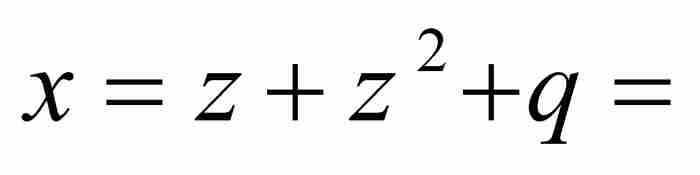
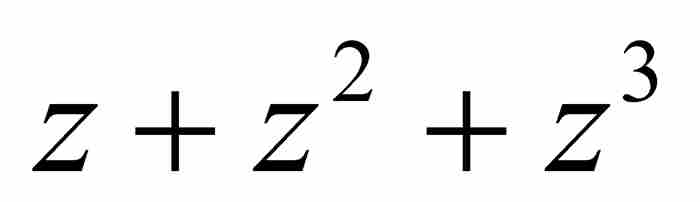 。
。
將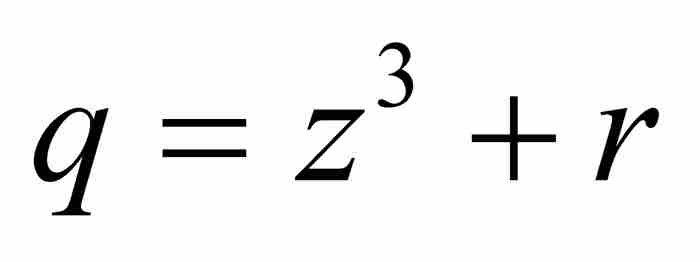 代入式(6),可以繼續這一推導過程。對於代數的單調乏味有著非凡忍耐力的牛頓似乎可以將這樣的計算(幾乎)無限地延續下去。但是,牛頓最終也樂於回過頭來審視結果,尋找某種一般的表達形式。牛頓這樣寫道:「讓考察停留在這裡,順便指出,當第5項或者第6項……為已知時,如果願意的話,一般來說,通過觀察這一過程的相似性,可以把推導隨意進行下去」。1
代入式(6),可以繼續這一推導過程。對於代數的單調乏味有著非凡忍耐力的牛頓似乎可以將這樣的計算(幾乎)無限地延續下去。但是,牛頓最終也樂於回過頭來審視結果,尋找某種一般的表達形式。牛頓這樣寫道:「讓考察停留在這裡,順便指出,當第5項或者第6項……為已知時,如果願意的話,一般來說,通過觀察這一過程的相似性,可以把推導隨意進行下去」。1
1 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 20。
對於我們的例子,這種考察表明,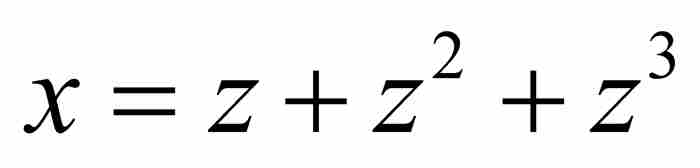
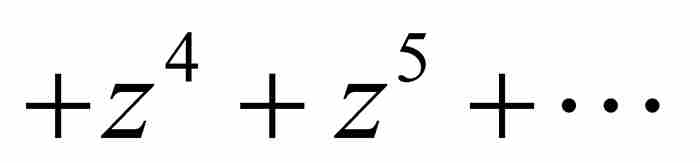 是我們開始時的級數
是我們開始時的級數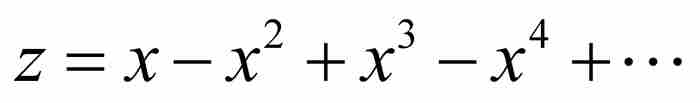 的逆級數。
的逆級數。
這個結果在什麼意義上是可靠的?畢竟,牛頓多次捨棄了絕大多數項,所以,這個答案的正確性還有多大的可信度呢?
下面的「檢驗」再次讓我們安心。原來的級數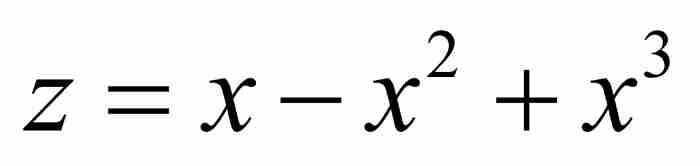
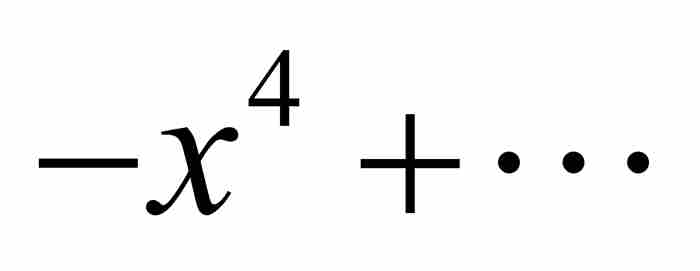 是公比為
是公比為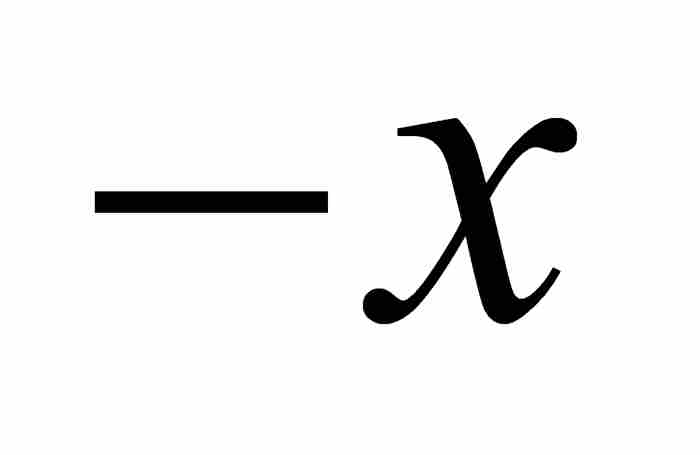 的等比級數,所以它的終極形式為
的等比級數,所以它的終極形式為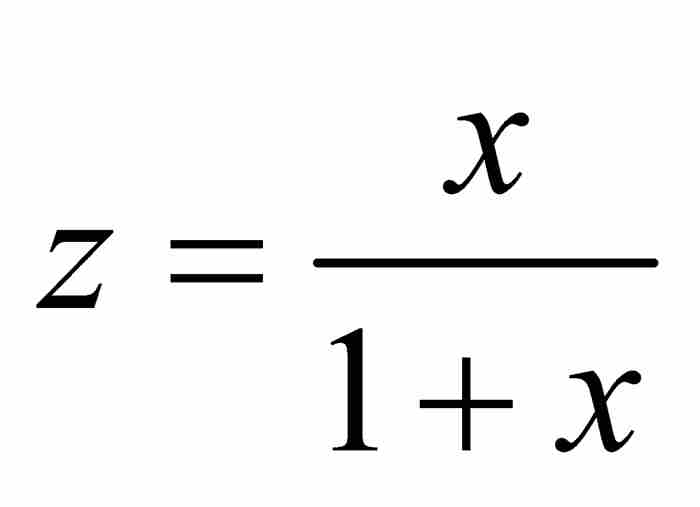 。因此,我們看出
。因此,我們看出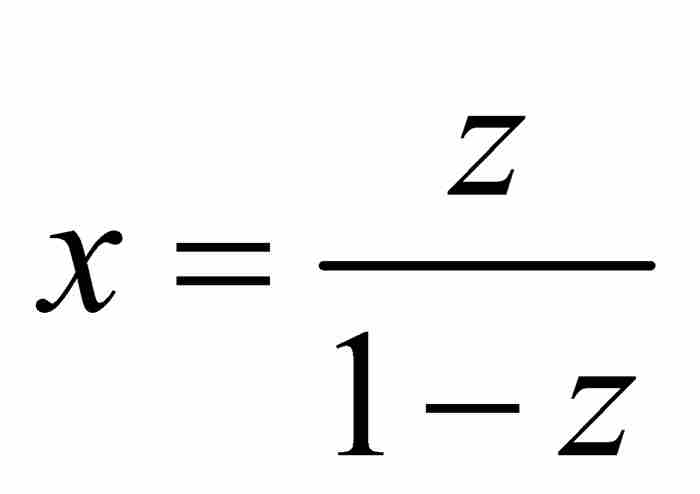 是等比級數
是等比級數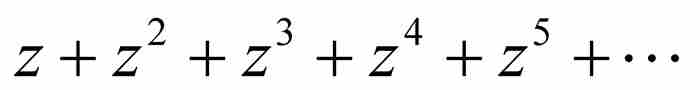 的和。這恰好是牛頓的推導過程給出的結果。一切推導看起來是有條不紊的。
的和。這恰好是牛頓的推導過程給出的結果。一切推導看起來是有條不紊的。
到目前為止,所討論的方法(廣義二項展開式和逆級數)將成為牛頓手中強有力的工具。然而,在我們真正評價這位大師的成果之前,還有最後一項必備知識。
《分析學》中求面積的法則
牛頓在1669年所寫的《分析學》一書中,承諾要論述求面積的方法,「我在很早以前已經發明了通過無窮項級數來計算曲線之下面積的方法」。1 這不是牛頓第一次提到他的流數發明,他在1666年10月撰寫的一本小冊子《流數簡論》中就說過同樣的話。《分析學》對那本小書做了修訂,展示了這位正在走向成熟的思想家的超人智慧。當代學者發現了一個奇特的現象:除了幾位幸運的同事外,神秘的牛頓沒有對公眾公開這份手稿。直到1711年,其中的許多結果已經由其他人發表之後,這份手稿才印製成書。雖然如此,更早的寫作年代和傑出的作者身份表明有理由把本書描繪為「也許是牛頓所有數學著作中最值得稱讚的」。2
1 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 3。
2 Derek Whiteside (ed.), Mathematical Papers of Isaac Newton, vol. 2,Cambridge University Press, 1968, p. 206。
該書以求「簡單曲線的面積」的三條法則的一個命題開始。在17世紀,英語中積分(quadrature)的含義是求面積,所以,這三條法則就是積分法則。
法則 1 簡單曲線的面積:如果
是曲線AD的函數,其中a是常數,m和n是正整數,那麼,區域ABD的面積為
(見圖1-1)。
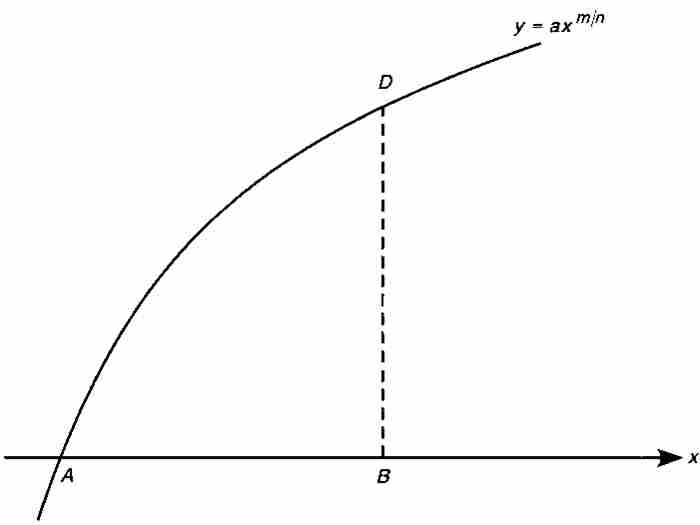
圖 1-1
這條法則的一種現代表述形式是,指定A為原點,B為(x, 0),曲線為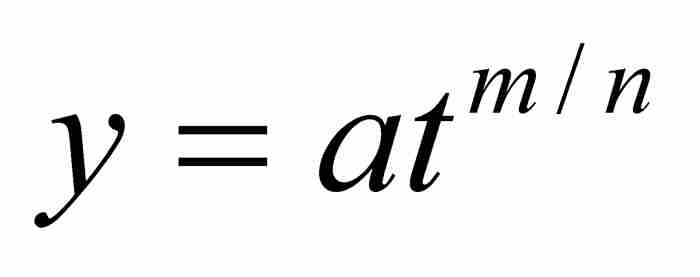 。於是,牛頓的命題變成
。於是,牛頓的命題變成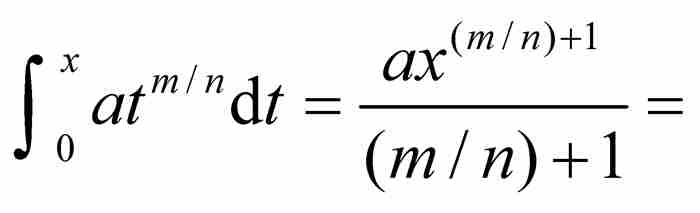
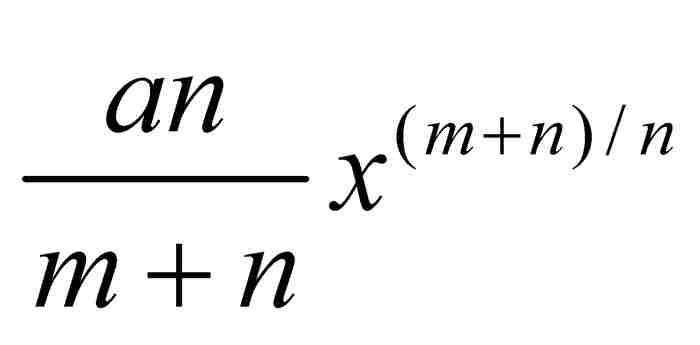 ,這正好是積分學中指數法則的一個特例。
,這正好是積分學中指數法則的一個特例。
僅僅到了《分析學》一書的最後,牛頓幾乎像事後反思一樣才注意到「留心的讀者」會想看到法則1的證明。3留心的讀者總是不乏其人的,所以我們在下面給出他的論證。
3 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 22。
如圖1-2所示,再次令曲線為AD以及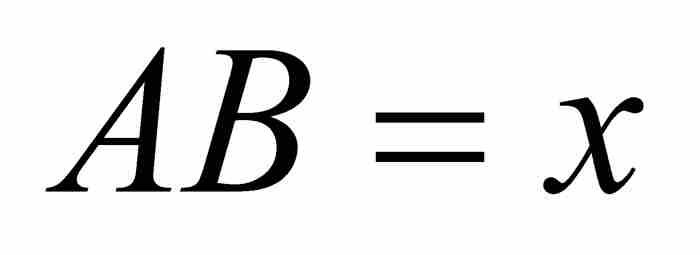 和
和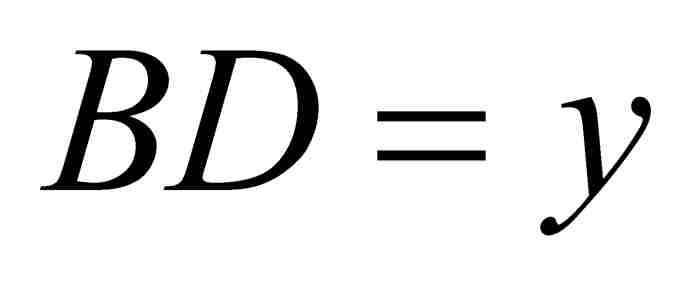 。牛頓假設曲線下的面積 ABD由z通過x的項的表達式給出。目標是求出y通過x表示的對應公式。按照一種現代的居高臨下的觀點,牛頓是從
。牛頓假設曲線下的面積 ABD由z通過x的項的表達式給出。目標是求出y通過x表示的對應公式。按照一種現代的居高臨下的觀點,牛頓是從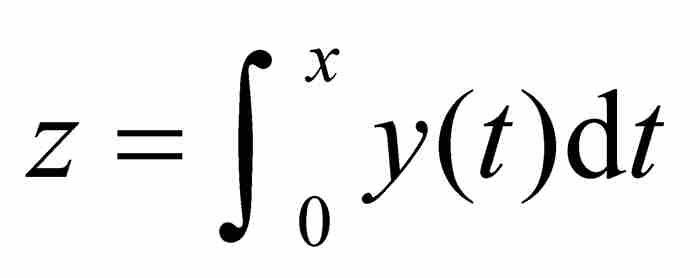 開始求解
開始求解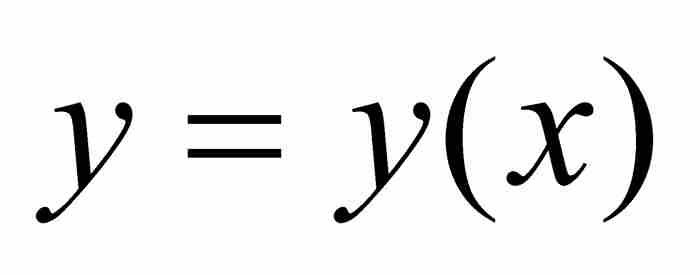 。在以幾個戲劇性的步驟結束之前,牛頓的推導過程綜合了幾何、代數和流數的方法。
。在以幾個戲劇性的步驟結束之前,牛頓的推導過程綜合了幾何、代數和流數的方法。
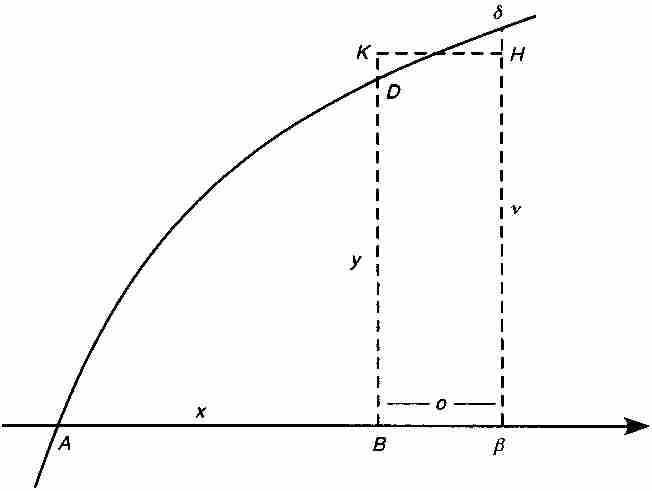
圖 1-2
首先,牛頓令β是橫坐標軸上同B相隔一小段距離o的點。因此線段Aβ的長度為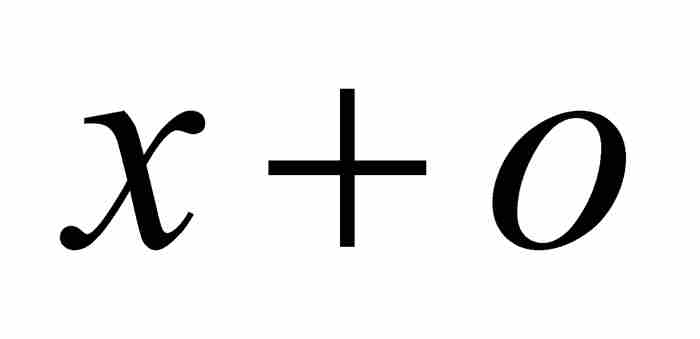 。他令z為面積ABD,不過為強調函數關係,我們有權用
。他令z為面積ABD,不過為強調函數關係,我們有權用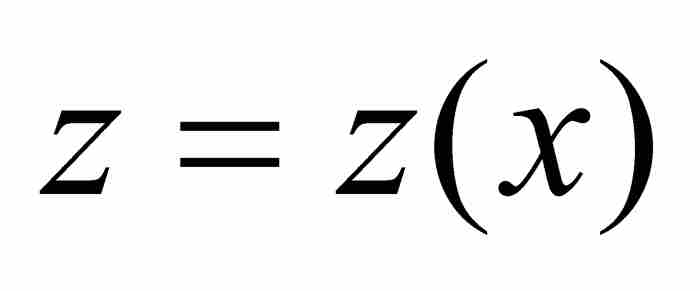 表示。因此,
表示。因此,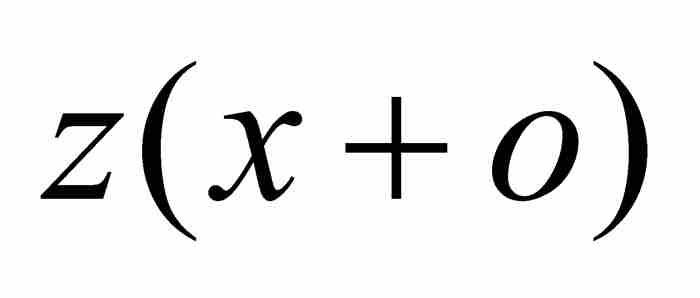 是曲線下的面積Aβδ。下一步,他引進高為v=BK=βH的矩形BβHK,他限定其面積恰好等於曲線下面的區域BβδD的面積。換句話說,BβδD的面積等於ov。
是曲線下的面積Aβδ。下一步,他引進高為v=BK=βH的矩形BβHK,他限定其面積恰好等於曲線下面的區域BβδD的面積。換句話說,BβδD的面積等於ov。
此時,牛頓指定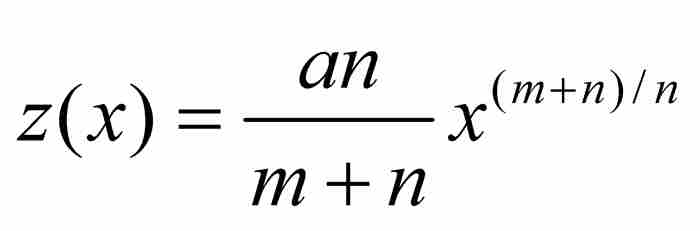 並繼續求z的瞬時變化率。為此,他考察了當x變小時x的變化對z的變化的影響。為書寫方便,他暫時令
並繼續求z的瞬時變化率。為此,他考察了當x變小時x的變化對z的變化的影響。為書寫方便,他暫時令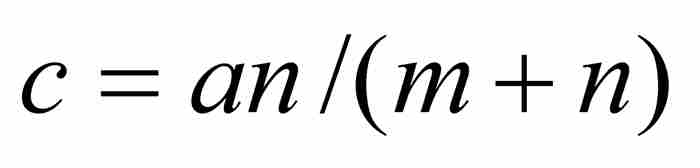 和
和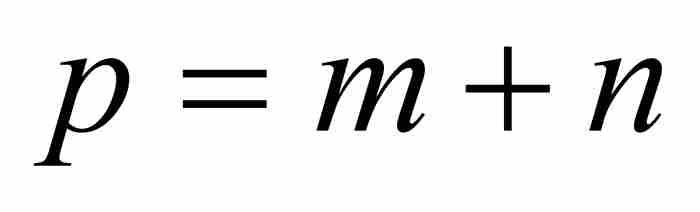 ,於是
,於是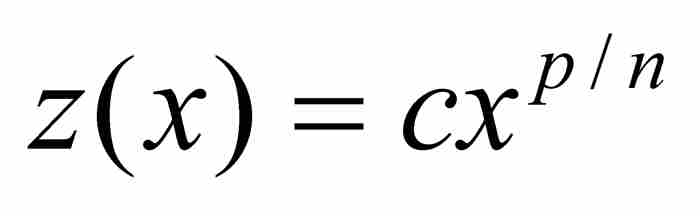 ,且
,且
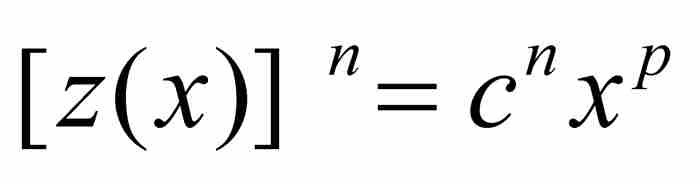 (7)
(7)
現在,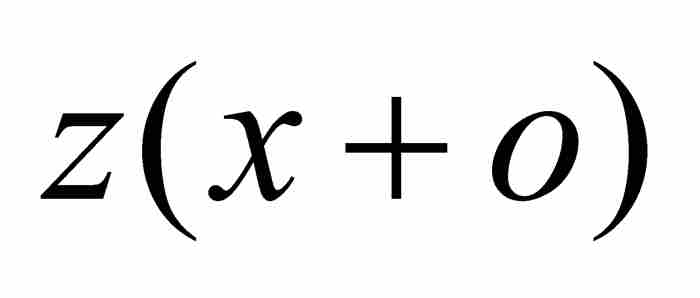 就是面積Aβδ。這個面積可以分解成面積ABD和BβδD。請注意,後者是矩形ov的面積,所以,牛頓斷定
就是面積Aβδ。這個面積可以分解成面積ABD和BβδD。請注意,後者是矩形ov的面積,所以,牛頓斷定 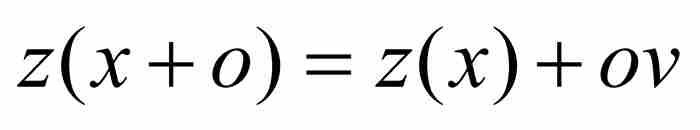 。代入式(7),得到
。代入式(7),得到
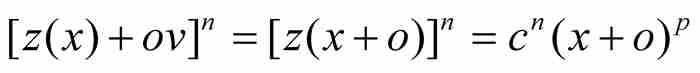
將等式左邊的二項式和右邊的二項式展開,得到
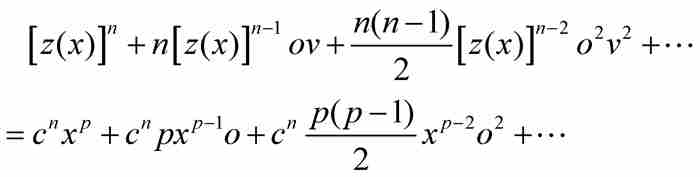
利用式(7)消去等式兩邊最左邊的項,併除以o,牛頓得到
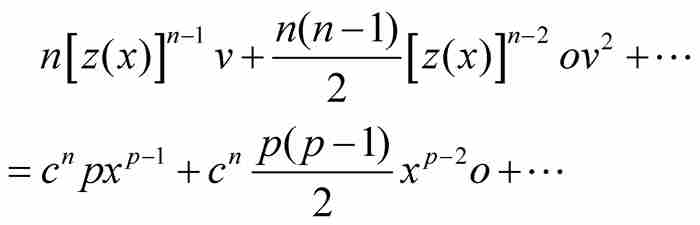 (8)
(8)
到這一步,他寫道:「如果我們假定Bβ為無限減小並消失的量,或者o為零,那麼,v和y在這種情況下相等,並且那些乘以o的項將消失」。4 他斷言,當o變成零時,式(8)中所有包含o的項也變成零。與此同時,v同 y相等,這就是說,圖1-2中矩形的高BK將等於原曲線的縱坐標BD。通過這種方式,式(8)變換成
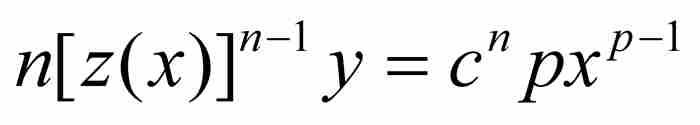 (9)
(9)
4 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 23。
現代讀者的反應很可能是,「別那麼快,艾薩克!」當牛頓用o作除數的時候,o無疑不等於零。但是過了一會,o就變成零了。一言以蔽之,這裡埋伏了隱患。這種零與非零的對應在隨後的一個多世紀一直困擾著分析學家們。本書後面將更多地討論這個問題。
不過,牛頓的推導仍然繼續進行。在式(9)中,他代換了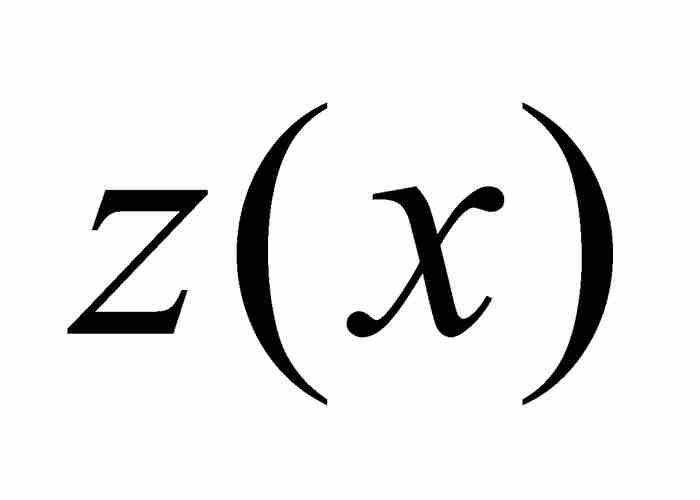 ,c和p並且解出
,c和p並且解出
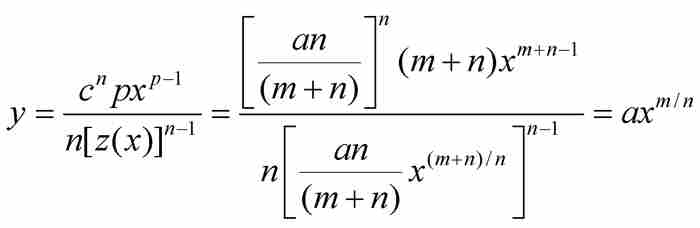
於是,牛頓從他的假設「ABD的面積為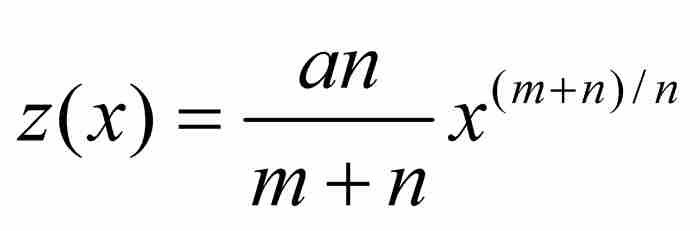 」出發,推出曲線AD必定滿足方程
」出發,推出曲線AD必定滿足方程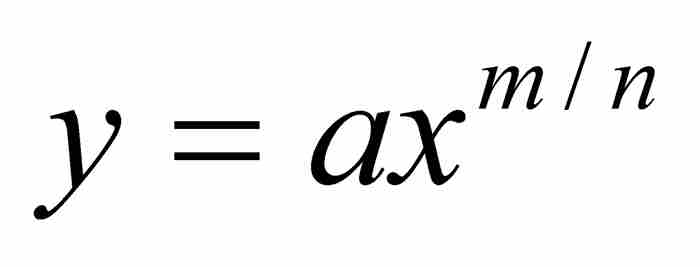 。從本質上說,他微分了積分。然後,在沒有進一步證明的情況下,他指出:「與此相反,如果
。從本質上說,他微分了積分。然後,在沒有進一步證明的情況下,他指出:「與此相反,如果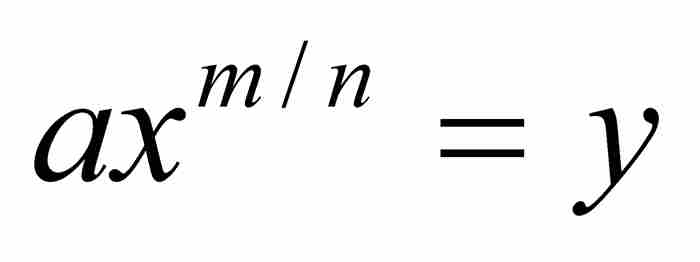 ,那麼就有
,那麼就有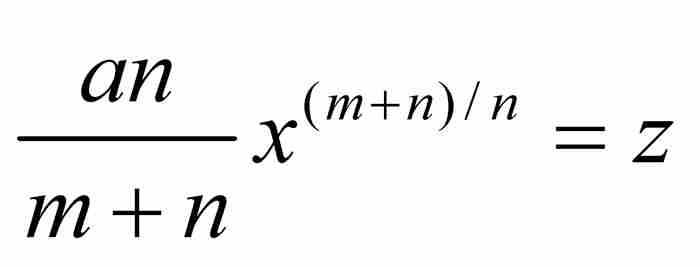 。」這就完成了他對法則1的證明。5
。」這就完成了他對法則1的證明。5
5 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 23。
這是一種特彆扭曲的邏輯。從曲線之下的面積積分z導出y的方程之後,牛頓斷言這種關係在相反的方向也存在,並且曲線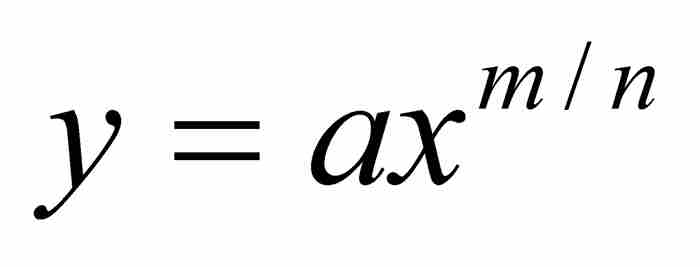 之下的面積就是
之下的面積就是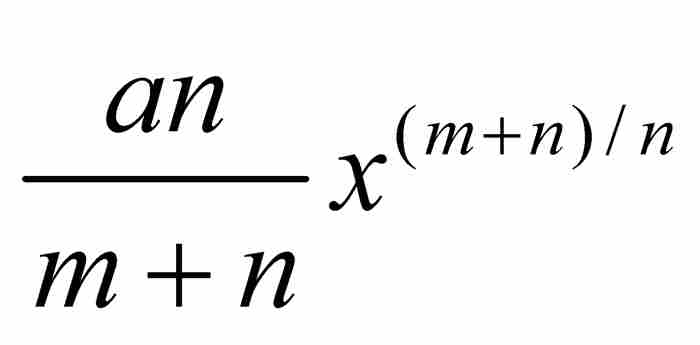 。這樣的論證給我們留下雜亂無章的感覺,因為其中包含很大的邏輯漏洞。牛頓數學論文集的編輯Derek Whiteside把這個求面積的證明恰當地描寫成「流數術的一種簡潔的難以理解的形式」。6 另一方面,記住這個起源是很重要的。牛頓在微積分漫長的創建過程的開頭就給出了法則1的證明。在他那個時代,這個證明是開山之作,並且他的結論是正確的。Richard Westfall在其評論中說,「然而概括地說,《分析學》確實展示了流數方法的整體範圍和威力」,看起來這是真實的。7
。這樣的論證給我們留下雜亂無章的感覺,因為其中包含很大的邏輯漏洞。牛頓數學論文集的編輯Derek Whiteside把這個求面積的證明恰當地描寫成「流數術的一種簡潔的難以理解的形式」。6 另一方面,記住這個起源是很重要的。牛頓在微積分漫長的創建過程的開頭就給出了法則1的證明。在他那個時代,這個證明是開山之作,並且他的結論是正確的。Richard Westfall在其評論中說,「然而概括地說,《分析學》確實展示了流數方法的整體範圍和威力」,看起來這是真實的。7
6 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. xiii。
7 Richard S. Westfall, Never at Rest, Cambridge University Press, 1980, p. 205。
無論如今的評判如何,牛頓當初是感到滿意的。牛頓在《分析學》中沒有給出證明的另外兩條法則如下:
法則 2 由簡單曲線構成的複雜曲線的面積:若y的值由若干項構成,那麼它的面積等於其中每一項的面積之和。8
8 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 4。
法則 3 所有其他曲線的面積:如果y的值或者它的任何項比上述曲線更複雜,那麼必須把它分解成更簡單的項……,然後應用前面兩條法則,就可以獲得欲求曲線的面積。9
9 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 6。
牛頓的第二條法則斷定有限項和的積分等於各項積分的和。他用了兩個例子來說明這條法則。第三條法則斷言,當遇到更複雜的表達式時,首先需要將其「化簡」成無窮級數,再通過第一條法則對級數的每一項求積分,然後再對結果求和。
最後這條法則是一個富有吸引力的主張。更恰當地說,這是最後一個前提條件,牛頓需要用它導出數學上的一個重大結果:一個角的正弦的無窮級數。出自《分析學》的這個重要定理是這一章最有意義的主題。
牛頓的正弦級數推導
考慮圖1-3中以原點為圓心和半徑等於1的圓的四分之一。同以前一樣,令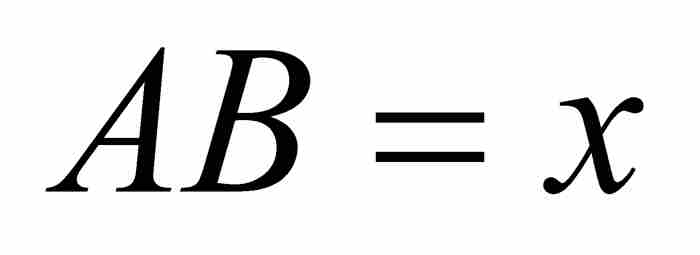 ,
,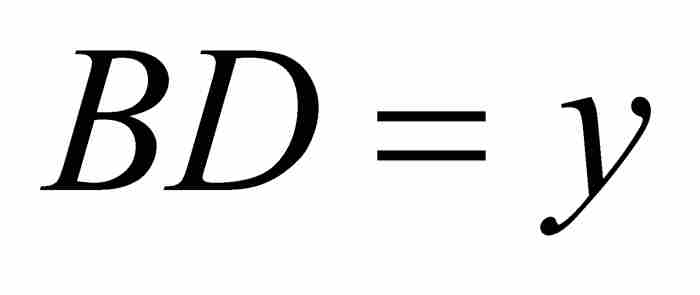 。牛頓的第一個目標是求圓弧αD的長度的表達式。1
。牛頓的第一個目標是求圓弧αD的長度的表達式。1
1 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, pp. 18-21。
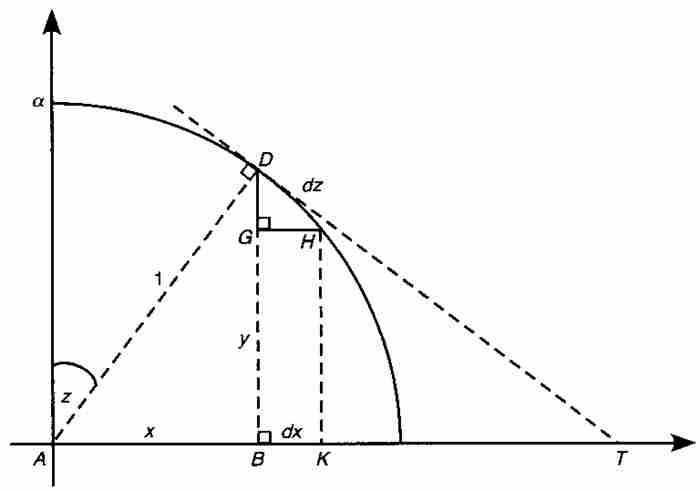
圖 1-3
從D引出圓弧的切線DT,並且令BK為「基底AB的增量」。在一種表示法中,我們令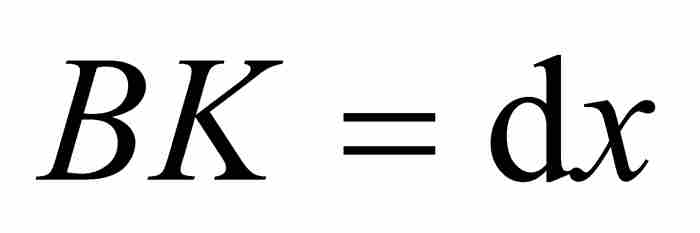 ,這成為牛頓之後的一種標準記號。這樣就建立了一個「無限小的」直角三角形DGH,牛頓把它的斜邊DH視為圓弧αD的增量。我們用
,這成為牛頓之後的一種標準記號。這樣就建立了一個「無限小的」直角三角形DGH,牛頓把它的斜邊DH視為圓弧αD的增量。我們用 表示,其中
表示,其中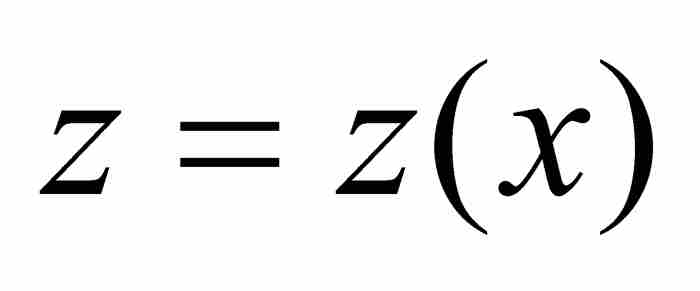 代表圓弧αD的長度。由於這一切都是發生在單位圓內,所以
代表圓弧αD的長度。由於這一切都是發生在單位圓內,所以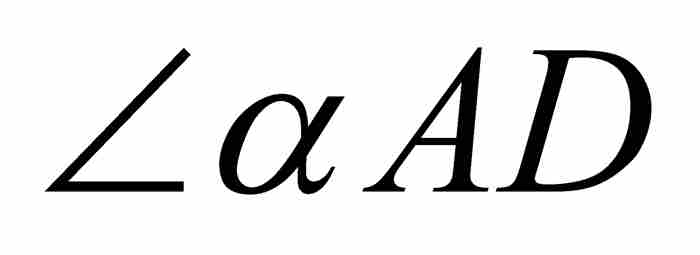 的弧度也是z。
的弧度也是z。
在這種情況下,無限小的三角形DGH與三角形DBT相似,所以有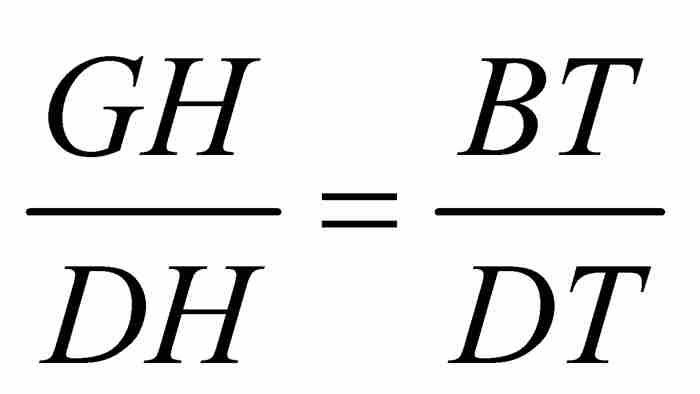 。此外,半徑AD與切線DT垂直,所以高線BD將直角三角形ADT分成兩個相似三角形DBT和ABD。由此推出,
。此外,半徑AD與切線DT垂直,所以高線BD將直角三角形ADT分成兩個相似三角形DBT和ABD。由此推出,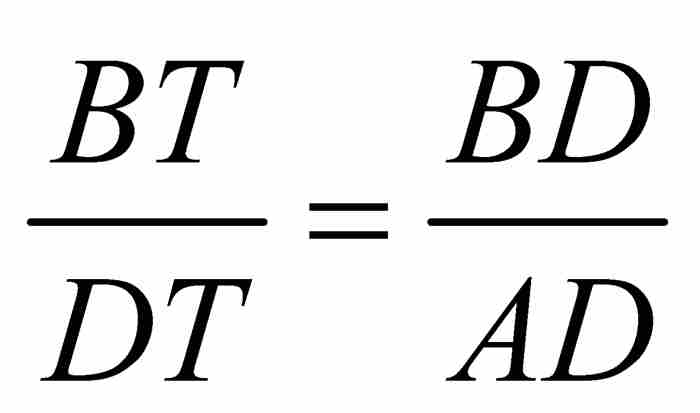 。從這兩個比例關係,我們可以推出
。從這兩個比例關係,我們可以推出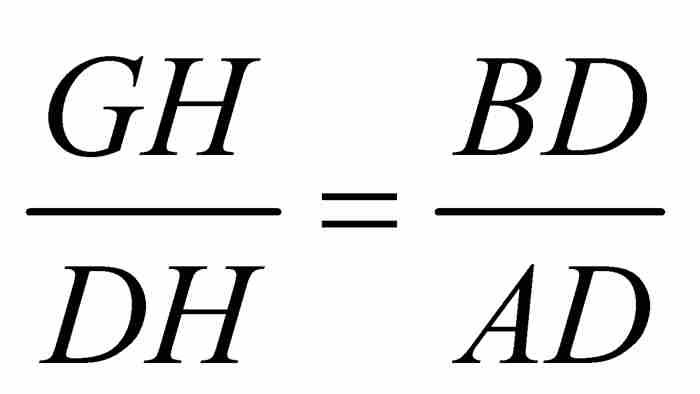 。採用上面的微分記號,可得
。採用上面的微分記號,可得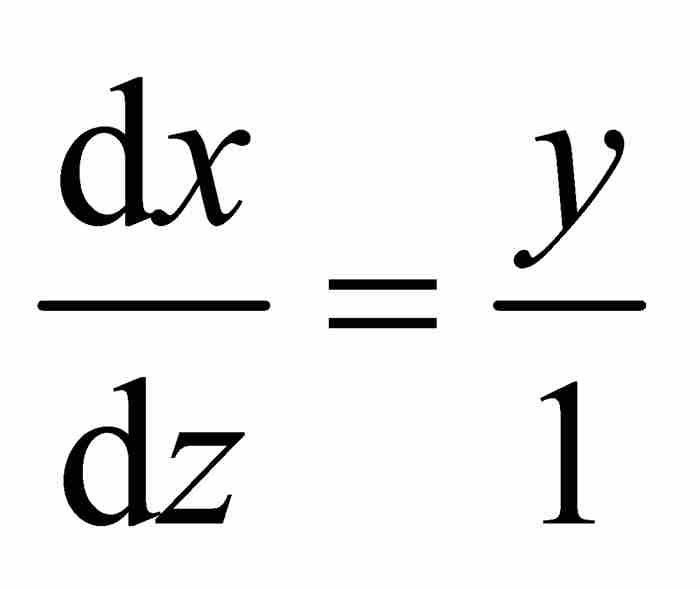 。因此,
。因此,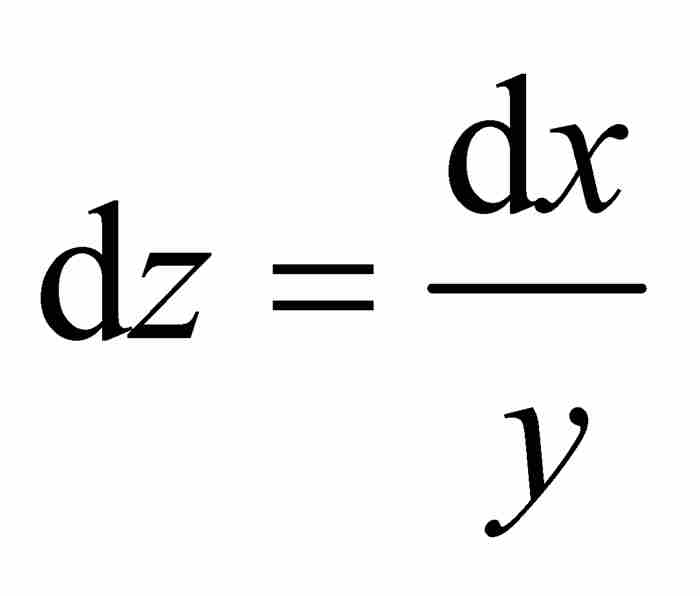 。
。
在下一步推導中牛頓利用圓的關係 ,得到
,得到 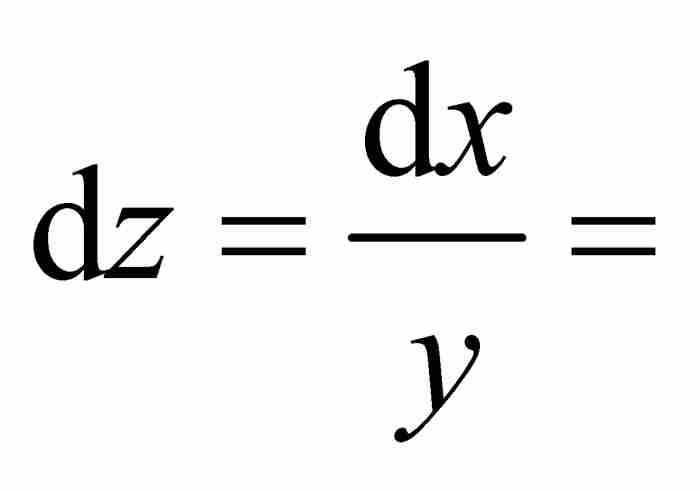
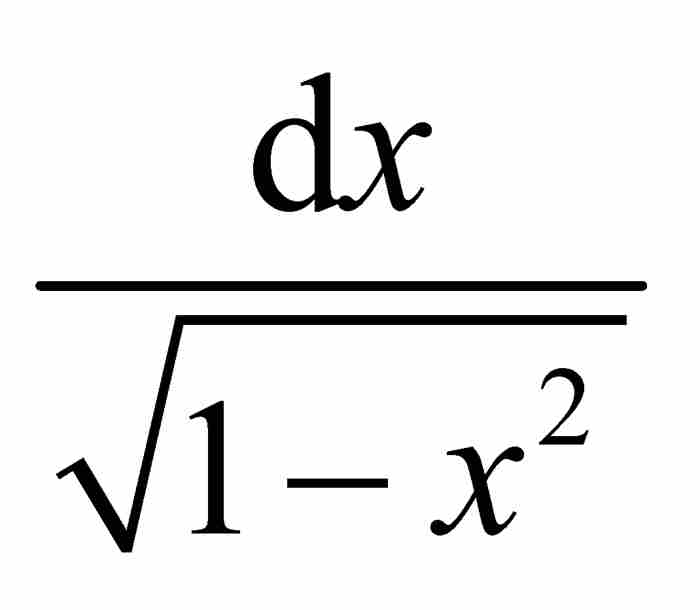 。像式(3)那樣展開
。像式(3)那樣展開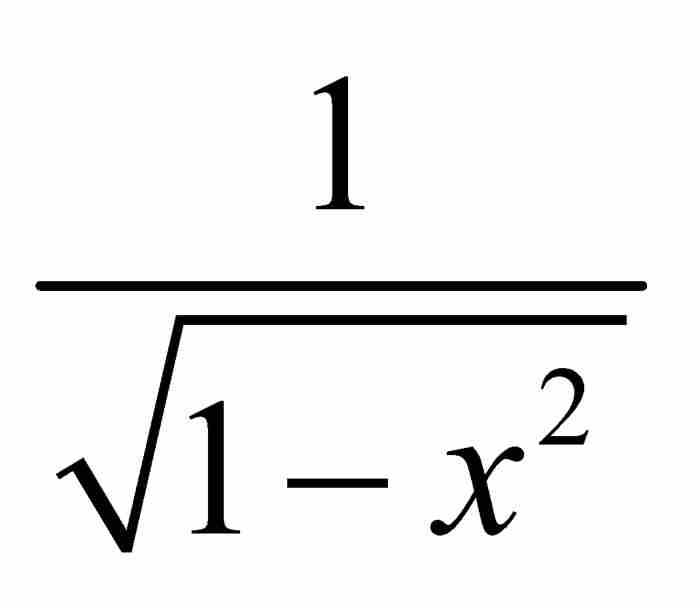 ,導出
,導出
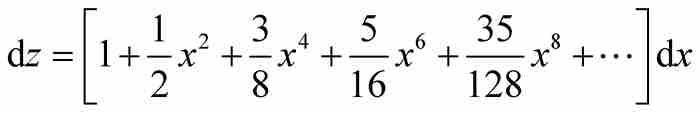
所以
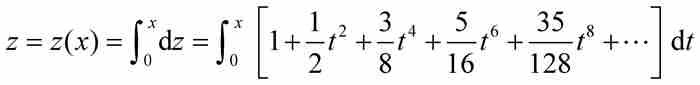
對這些單獨的乘方項求面積,並用法則3對結果求和,牛頓得到圓弧αD的弧長為
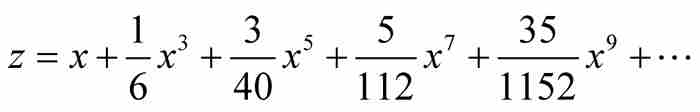 (10)
(10)
再度審視圖1-3,我們看到z不僅僅是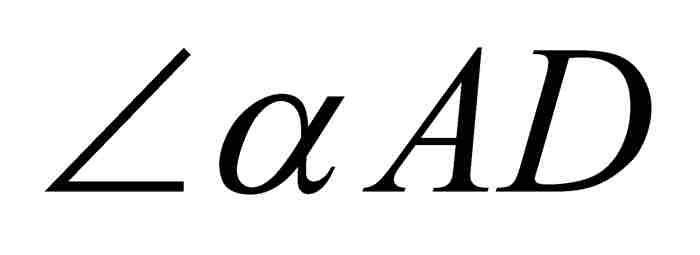 的弧度,也是
的弧度,也是 的弧度。由三角形ABD可知,
的弧度。由三角形ABD可知,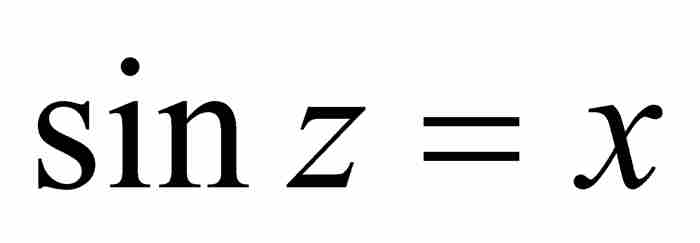 ,所以
,所以
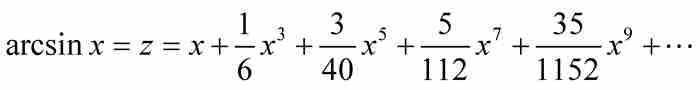
因此,從代數表達式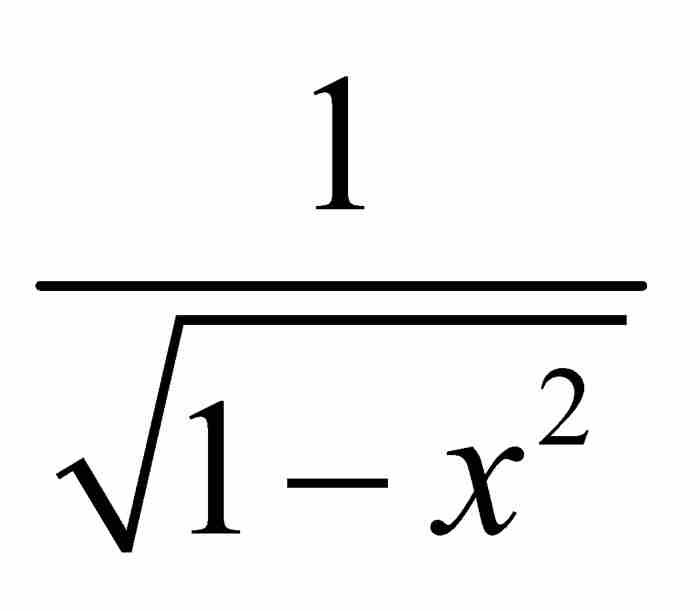 開始,牛頓利用他的廣義二項展開式和基本的積分推導出反正弦的級數,這是本質上更為複雜的一個關係式。
開始,牛頓利用他的廣義二項展開式和基本的積分推導出反正弦的級數,這是本質上更為複雜的一個關係式。
然而,牛頓還有一個錦囊妙計。他不去求用橫坐標(x)表示的弧長(z)的級數,而是尋找相反的過程。他寫道:「如果需要從已知弧長αD求AB的正弦,那麼我對上面導出的表達式求根。」 2 就是說,牛頓利用他的逆過程,將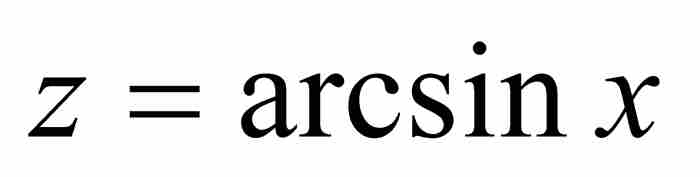 的級數轉換成
的級數轉換成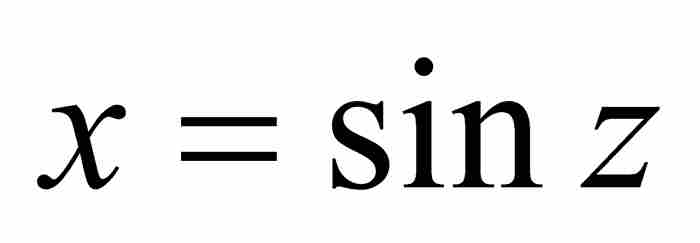 的級數。
的級數。
2 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 20。
按照前面描述的方法,我們從把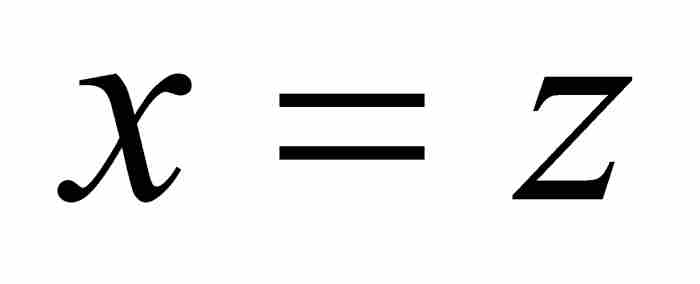 作為第一項開始。為把級數展開推進到下一步,將
作為第一項開始。為把級數展開推進到下一步,將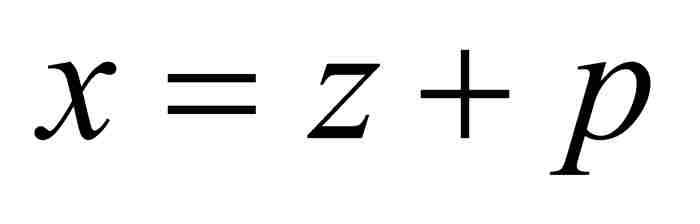 代入式(10),並且解出
代入式(10),並且解出
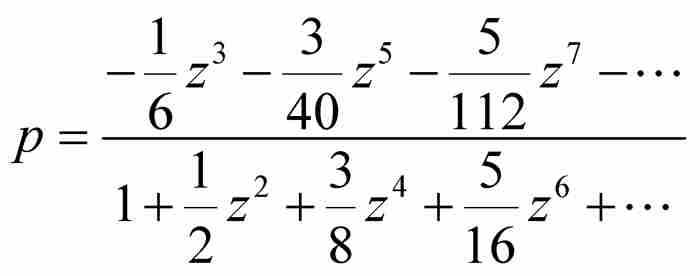
我們僅從這個解中保留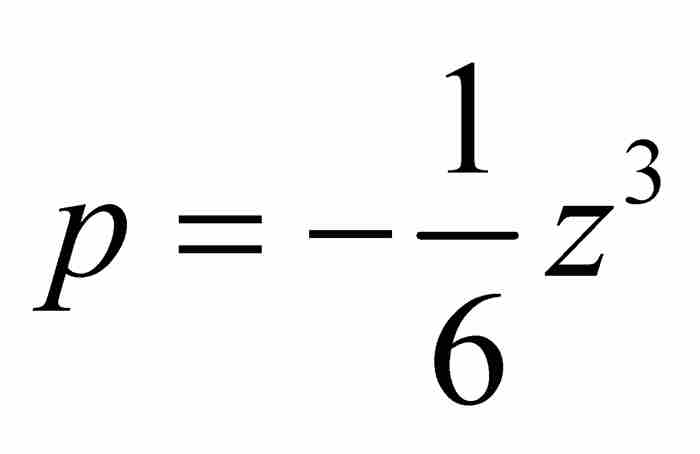 。這樣就將級數擴展成
。這樣就將級數擴展成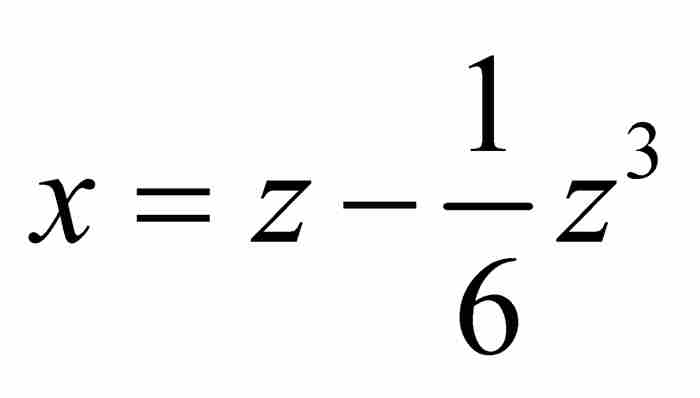 。下一步引進
。下一步引進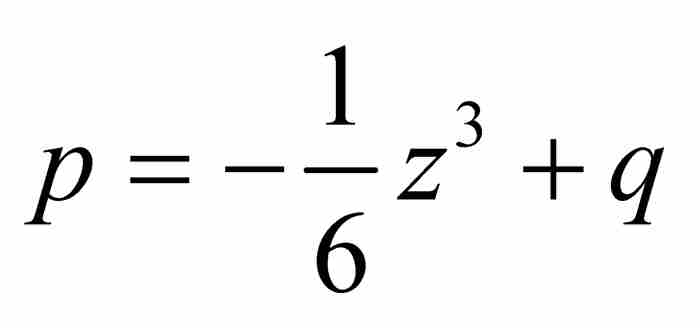 ,繼續這個逆過程,解出
,繼續這個逆過程,解出
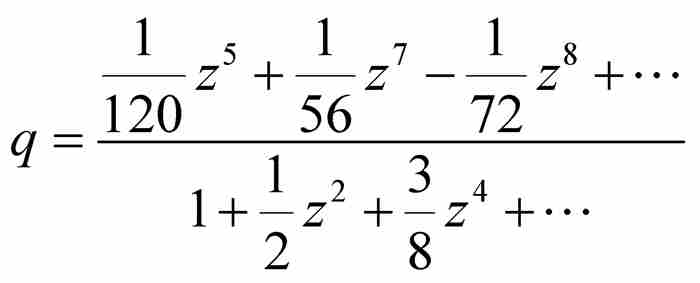
或者化簡為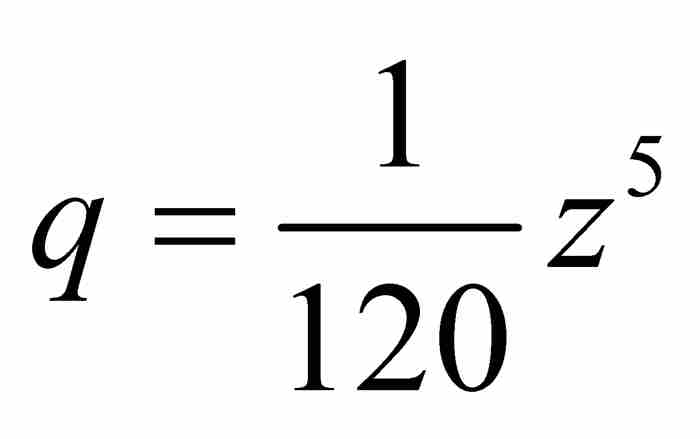 。到這一步,級數變成
。到這一步,級數變成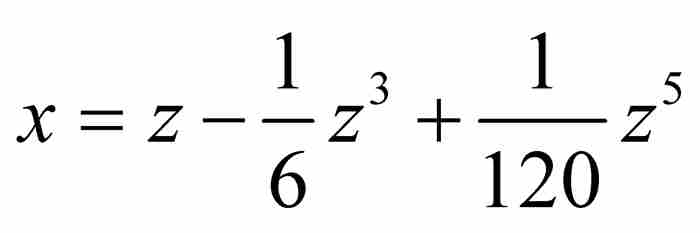 ,並且,也許像牛頓所說的那樣,我們「繼續隨意地」推導下去,直至發現級數項的通用模式,然後書寫下分析學中最重要的一個級數:
,並且,也許像牛頓所說的那樣,我們「繼續隨意地」推導下去,直至發現級數項的通用模式,然後書寫下分析學中最重要的一個級數:
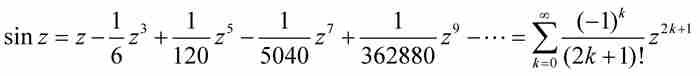
為了獲得更準確的曲線弧長,牛頓又推導了餘弦級數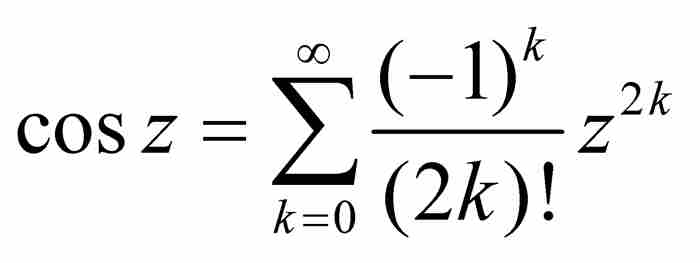 。按照Derek Whiteside的說法,「關於正弦和餘弦的這些級數第一次出現在歐洲人的手稿中」。3
。按照Derek Whiteside的說法,「關於正弦和餘弦的這些級數第一次出現在歐洲人的手稿中」。3
3 Derek Whiteside (ed.), Mathematical Papers of Isaac Newton, vol. 2,Cambridge University Press, 1968, p. 237。

牛頓的正弦級數和餘弦級數(1669)
對我們來說,這種推導所兜的圈子看起來是不可思議的。我們現在把正弦級數視為不過是泰勒公式和微分學的一個微不足道的推論而已。所以我們自然而然地以為它一直就是這樣簡單的。但是,正如我們所見,牛頓克服了重重困難才得到這個結果。他運用了積分法則而不是微分法則;他從(我們認為)偶然的反正弦級數產生正弦級數;同時,他需要運用他所提出的複雜的逆過程方案來完成全部推導。
這個歷史片段提醒我們,數學並不是按照現在教科書中的方式發展的。相反,它是通過斷斷續續地在出乎意料的驚喜中發展起來的。事實上,那是相當有趣的,因為歷史在一下子變得有意義、美好和出乎意料的時候,它是極具吸引力的。
談到出乎意料這個話題,我們就Derek Whiteside在上面那段話中的評判補充一句。看起來牛頓並不是第一個發現正弦級數的人。印度數學家尼拉坎塔(1445—1545)在公元1545年描述過這個級數,並且把它歸功於更久遠的前輩馬達維(生活在公元1400年前後)。關於這些發現和印度數學中的優良傳統的敘述可以從文獻4和5中查到。但是,這些成果在牛頓活躍的時代的歐洲自然不為人們所知。
4 David Bressoud, 「Was Calculus Invented in India?」 The College Mathematics Journal, vol. 33 (2002), pp. 2-13。
5 Victor Katz, A History of Mathematics:An Infroduction, Harper-Collins, 1993, pp. 451-453。
我們以兩點評論作為本章的結束語。第一,牛頓的《分析學》是一本真正的數學經典,是任何一位對微積分的歷程感興趣的人都應擁有的讀物。從中可以瞥見這位歷史上最具創造力的思想家在其才智發展的早期階段的情況。
第二,用現在的眼光看來,一場轟轟烈烈的革命開始了。年輕的牛頓以其超越時代的專業才能和洞察力把無窮級數和流數法結合起來,將數學的前沿推向若干新的發展方向。與他同時代的詹姆斯·格雷戈裡(1638—1675)評論過去的初等方法對於產生同樣關聯的這些新方法,就如同「黎明的晨曦對於正午的陽光」。6 正如我們在後面幾章將要多次看到的,格雷戈裡這種令人陶醉的描述是恰如其分的。同時,第一個走向這條激動人心的道路的人是牛頓,他確實不愧為「一位具有非凡天賦和卓越才能的人物」。
6 C. Gerhardt (ed.), Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern, vol. 1, Mayer & Muller Berlin, 1899, p. 170。
