
戈特弗裡德·威廉·萊布尼茨(1646—1716)
微積分的兩位創建者都因為在其他的方面也有建樹而更聞名,這也許是獨一無二的。在公眾的心目中,艾薩克·牛頓往往被看成一位物理學家,而微積分的共同創建者戈特弗裡德·威廉·萊布尼茨則多半被認為是一位哲學家。這既令人不悅又讓人欣喜,不悅是因為這表明人們無視他們在數學上的貢獻,而欣喜是由於人們公認創建微積分需要超越一般天才的奇才。
萊布尼茨興趣廣泛,貢獻突出,具有淵博的知識。除了哲學和數學,他在歷史、法學、語言、神學、邏輯學和外交方面都有傑出的成就。在年僅27歲時,萊布尼茨就憑借他發明的一台機械計算器加入了英國皇家學會,這台可以進行加、減、乘、除運算的機器以其複雜性被公認為一次革命。1
1 Joseph E. Hofmann, Leibniz in Paris: 1672-1676, Cambridge University Press, 1974, pp. 23-25和p. 79。
雖然晚於牛頓,並且出生在另一個國度,萊布尼茨還是和牛頓一樣有著一段熱烈進行數學研究的時期。牛頓在17世紀60年代中期已經在劍橋大學建立了他的流數思想,而萊布尼茨是在十年之後在巴黎履行外交使命時完成他自己的奠基工作的。這使牛頓捷足先登,也讓牛頓和他的同胞們後來認定這是事關優先權的唯一憑據。但是當萊布尼茨發表他的微積分成果時,牛頓的《分析學》和其他論文仍然以手稿的形式塵封著。關於接著發生的微積分發明權應該歸功於哪一位的爭論,已有很多著述,而且這並不是一個動聽的故事。2上百年來,現代學者們終於抹去了國家和個人的感情因素,認定牛頓和萊布尼茨各自獨立創建了微積分。像水到渠成的一種觀念的產生一樣,微積分到了「呼之欲出」的時刻,只是需要極端敏銳的和總攬其成的思想將它變成現實。牛頓恰恰具有這種思想。
2 例如,參考Rupert Hall, Philosphers at War, Cambridge University Press, 1980。
毫無疑問,萊布尼茨也具有這種思想。在1672年,他到巴黎擔任外交官之前,萊布尼茨還是一個被認為對「閱讀冗長的數學證明」缺乏耐心的新手。3他不滿足於自己的知識,花費時間填補缺口,大量閱讀令人敬仰的數學家們的著作,遠至古代的歐幾里得(公元前3世紀前後),近至他那個時代的帕斯卡(1623—1662)、巴羅以及他一度師從的克裡斯琴·惠更斯(1629—1695)。開始的時候困難重重,但是萊布尼茨堅持了下來。他後來回憶說,儘管他還有很多不足,但是「不知從哪裡來的自信讓我堅信,只要努力我就可以成為他們中的一員」。4
3 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 11。
4 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p.12。
萊布尼茨取得的成功是激動人心的。他在一段回憶文章中寫道,他很快就「作好進行獨立研究的準備,因為我閱讀數學文獻就如同別人閱讀浪漫的小說一樣輕鬆」。5 在幾乎是狼吞虎嚥地吸收同時代的人的成果之後,萊布尼茨把他們遠遠地拋在後面,創造了微積分,從而使他在數學上贏得名垂青史的業績。
5 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p.12。

萊布尼茨關於微分學的第一篇論文(1684)
與英吉利海峽對岸的牛頓不同,萊布尼茨願意發表成果。微積分的第一個刊載形式是萊布尼茨1684年撰寫的論文,這篇論文帶有一個冗長的標題Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas, nec irrationales quantitates moratur; et singulare pro illis calculi genus,翻譯過來是《一種求極大值與極小值以及求切線的新方法,它也適用於有理量與無理量以及這種新方法的奇妙類型的計算》。6 既然涉及求極大值與極小值以及求切線問題,毫無疑問,萊布尼茨的這篇文章是介紹微分法的。兩年以後他又發表了另一篇介紹積分法的文章。即使處於早期階段,萊布尼茨不但構造和整理了許多微積分的基本法則,而且已經用 表示 x 的微分和用
表示 x 的微分和用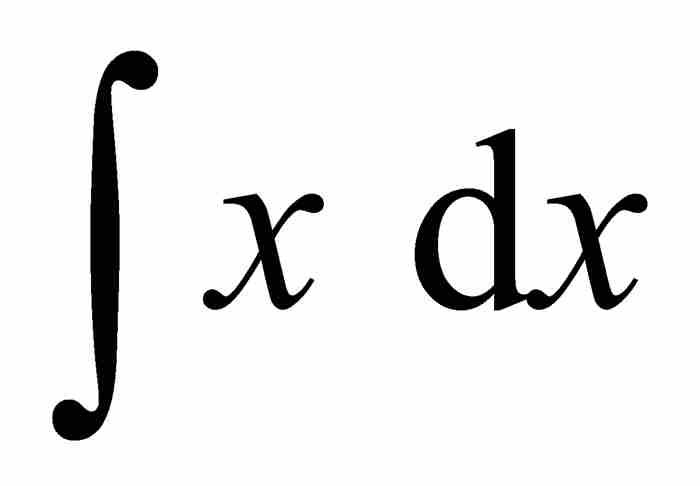 表示 x 的積分。他的卓越才能之一,正是後來拉普拉斯所說的提供了「一種非常恰當的符號」。7
表示 x 的積分。他的卓越才能之一,正是後來拉普拉斯所說的提供了「一種非常恰當的符號」。7
6 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard University Press, 1969, pp. 272-280。
7 Robert E. Moritz (ed.), Memorabilia Mathematica, MAA, 1914, p. 323。
在這一章,我們考察他在1673年至1674年間證明的兩個定理。所討論的大部分材料來自萊布尼茨的專著《微分學的歷史和起源》,書中敘述了他創建微積分過程中發生的事情。8 我們討論的第一個定理是很抽像的所謂變換定理。在它的推導中攙雜著幾何技巧,雖然這一點現在不能引起人們的興趣,而在當初卻顯示了他的數學天分,產生了我們現在所說的分部積分法的初期形式。第二個結果是第一個結果的推論,被稱為「萊布尼茨級數」。如前面一章討論的牛頓的成果一樣,這種級數展開和基本積分方法的結合產生一個重要的和妙不可言的結果。
8 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, pp. 22-58。
變換定理
在17世紀中期,計算曲線之下的面積是一個熱門話題,這也是萊布尼茨變換定理的主題。在圖2-1中,假定我們要計算曲線AB下面的面積。萊布尼茨將這個區域的面積想像成是由無限多個無限小的矩形構成的。每個矩形的寬度為 ,長度為y,其中y隨曲線AB的形狀變化而改變。
,長度為y,其中y隨曲線AB的形狀變化而改變。
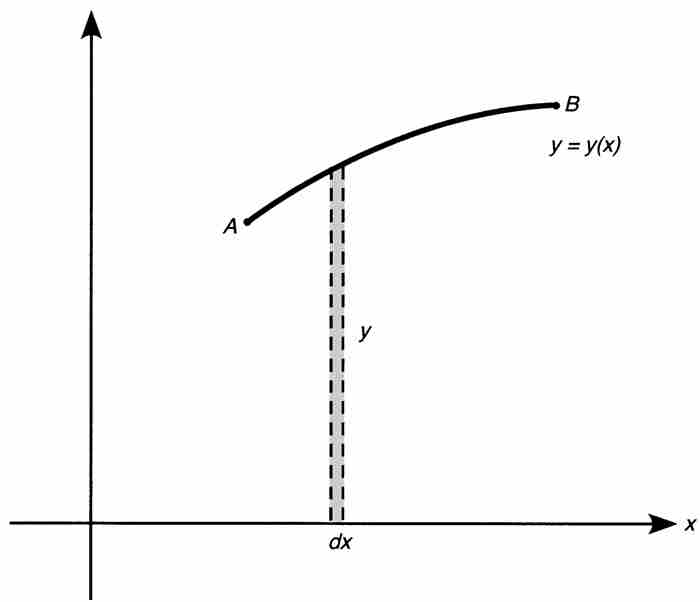
圖 2-1
在我們看來,萊布尼茨的 的性質是不明確的。在17世紀,
的性質是不明確的。在17世紀, 被看作是最小的可能長度,一個無限小的不可能再分的長度。但是怎麼可能有這樣的事情呢?很明顯,任意長度,即使是刀刃一樣薄的長度,也可以分為兩半。萊布尼茨關於這一點的解釋無助於概念的澄清,他對問題的說明是難以理解的。下面是萊布尼茨在1684年之後的一份手稿中的一段文字:
被看作是最小的可能長度,一個無限小的不可能再分的長度。但是怎麼可能有這樣的事情呢?很明顯,任意長度,即使是刀刃一樣薄的長度,也可以分為兩半。萊布尼茨關於這一點的解釋無助於概念的澄清,他對問題的說明是難以理解的。下面是萊布尼茨在1684年之後的一份手稿中的一段文字:
關於……無限小,我們理解為……某種無限的小,所以每次分割本身都成為一個級別,只不過不是一個最後的級別。如果有誰希望將這些[無限小]理解為最終的事物……,那麼,這也是可以的,而且也不會陷入關於延伸範圍或者一般而論的無限連續統或者無限小的真實性的爭論中,即使他認為這樣的事是完全不可能的。1
1 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 150。
讀者不必尋找這種概念的澄清,更無需自己去澄清。萊布尼茨看來選擇了邏輯上的權宜之計,他作出補充,即使這些不可份量的性質尚不確定,它們依然可以作為「用於計算的有力工具」。我們再次看到了令後來的分析學家們進退維谷的數學泥潭。但是在1673年,萊布尼茨急切地向前推進,將這個邏輯上的問題留給下一代人解決。
回到圖2-1,我們看到無限小矩形的面積為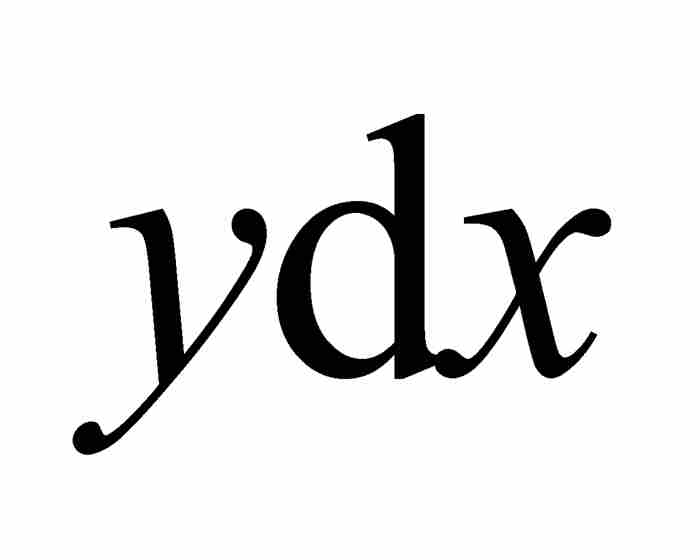 。為計算曲線AB下面的面積,萊布尼茨對這無窮多個面積求和。他選用伸長的「S」——代表「summa」(求和)——作為表示這個過程的記號。因此,這個面積表示成
。為計算曲線AB下面的面積,萊布尼茨對這無窮多個面積求和。他選用伸長的「S」——代表「summa」(求和)——作為表示這個過程的記號。因此,這個面積表示成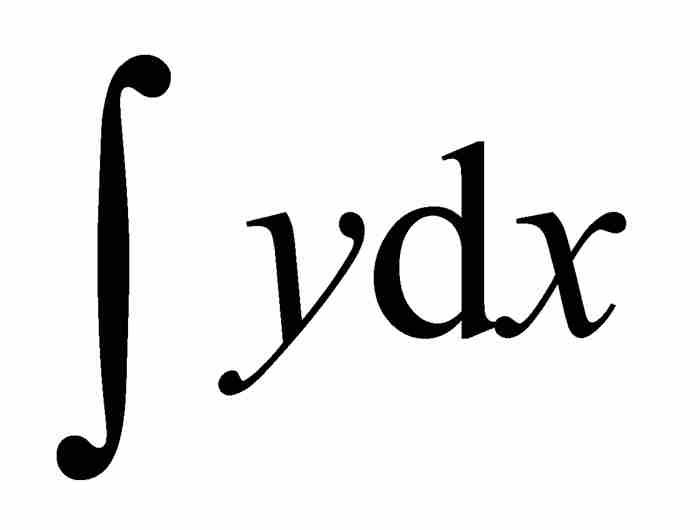 。從此以後,他的積分符號成了微積分的「標誌」,向所有見到它的人宣告高等數學來臨了。
。從此以後,他的積分符號成了微積分的「標誌」,向所有見到它的人宣告高等數學來臨了。
提出一個表示面積的記號是一回事,而掌握怎麼計算面積完全是另一回事。萊布尼茨的變換定理就是以解決這個計算問題作為目標。
圖2-2說明了他的思想,其中再次顯示曲線AB,求它下面的面積是我們的目標。P是曲線上任意一點,其坐標為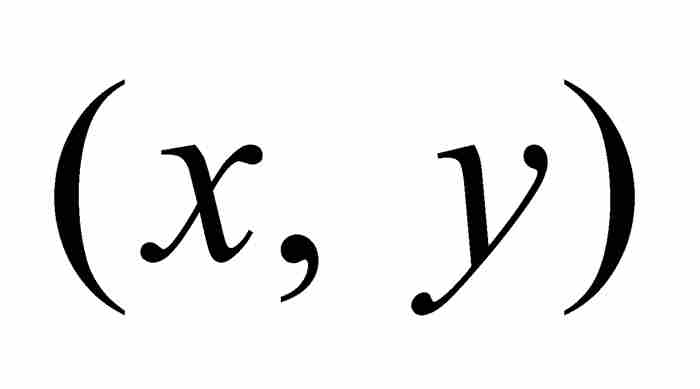 。萊布尼茨在P點畫出切線 t,與縱坐標軸相交於點T(0, z)。萊布尼茨解釋這個構造時說明「求一條切線意味著畫一條直線連接曲線上距離無限小的兩個點」。2 令
。萊布尼茨在P點畫出切線 t,與縱坐標軸相交於點T(0, z)。萊布尼茨解釋這個構造時說明「求一條切線意味著畫一條直線連接曲線上距離無限小的兩個點」。2 令 為x的無限小的增量,他建立一個無限小的直角三角形,以切線上的線段PQ為斜邊,邊長分別為
為x的無限小的增量,他建立一個無限小的直角三角形,以切線上的線段PQ為斜邊,邊長分別為 ,
, ,
, 的三角形放大後的圖形顯現在圖2-3中。令α為切線的傾角。
的三角形放大後的圖形顯現在圖2-3中。令α為切線的傾角。
2 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard University Press, 1969, p. 276。
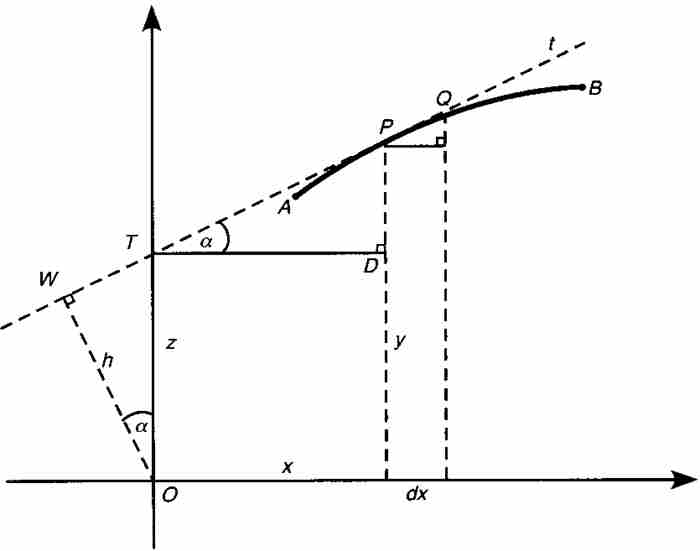
圖 2-2
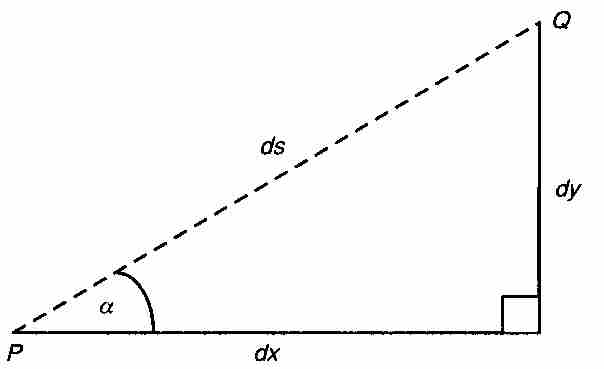
圖 2-3
萊布尼茨強調,「雖然這個三角形是不確定的(無限小),但是……總可能找到一個相似於它的確定的三角形」。3 當然,有人會疑惑一個無限小三角形怎麼可能同任何東西相似,但是這不是糾纏於細枝末節的時候。萊布尼茨把圖2-2中的 看成與圖2-3中的無限小三角形相似。於是有
看成與圖2-3中的無限小三角形相似。於是有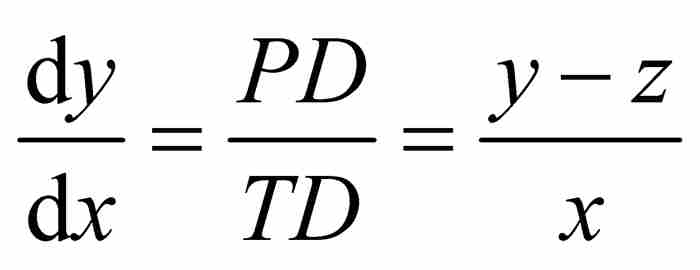 ,求解得到
,求解得到
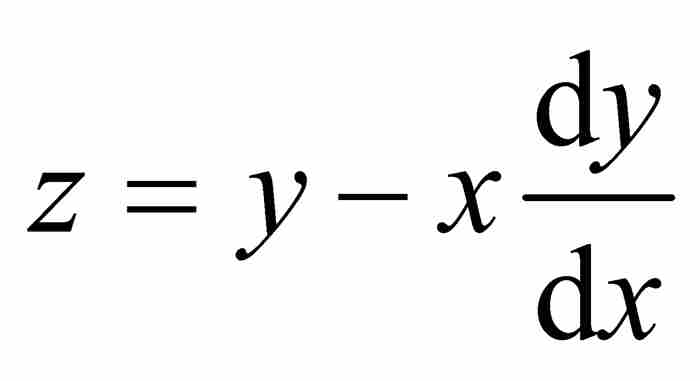 (1)
(1)
3 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 39。
下一步,萊布尼茨向左延長切線PT,並且從原點引出同這條延長線垂直的長度為 h 的線段OW(見圖2-2)。由於 的值是α,可知
的值是α,可知 的值為
的值為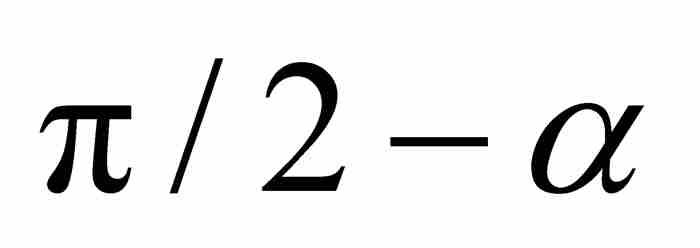 ,所以
,所以 的值也是α。這使得
的值也是α。這使得 相似於無限小的那個三角形,於是得到另一個比例關係
相似於無限小的那個三角形,於是得到另一個比例關係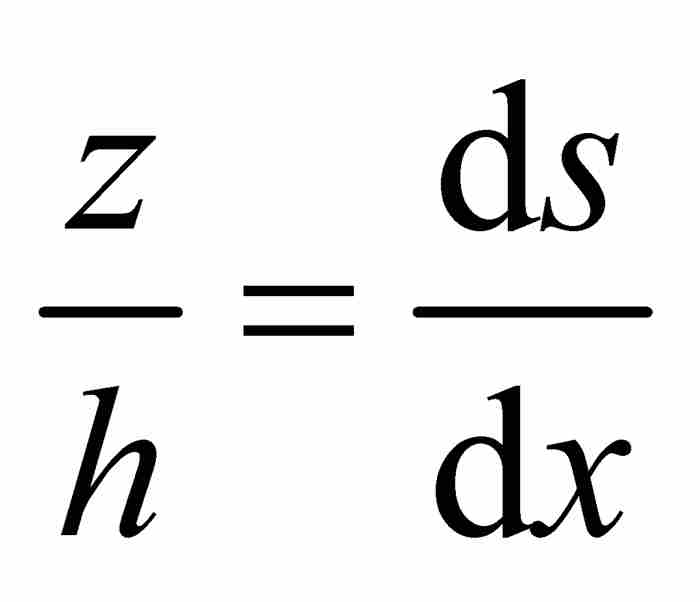 ,我們由此推出
,我們由此推出
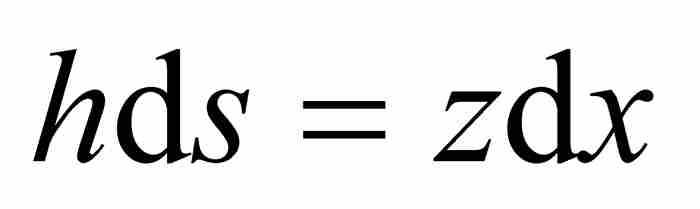 (2)
(2)
萊布尼茨然後畫出從原點輻射出的 ,以無限小三角形的斜邊PQ為底邊。為避免使圖2-2變得更為雜亂,我們將這個特別的三角形重新畫在圖2-4中。
,以無限小三角形的斜邊PQ為底邊。為避免使圖2-2變得更為雜亂,我們將這個特別的三角形重新畫在圖2-4中。

圖 2-4
到這一步讀者也許會想,萊布尼茨已經隨波逐流地迷失在毫無目標的三角形的汪洋大海之中。然而,事實上,這個無限小斜三角形OPQ卻成為他的變換定理的核心。由於三角形的底邊為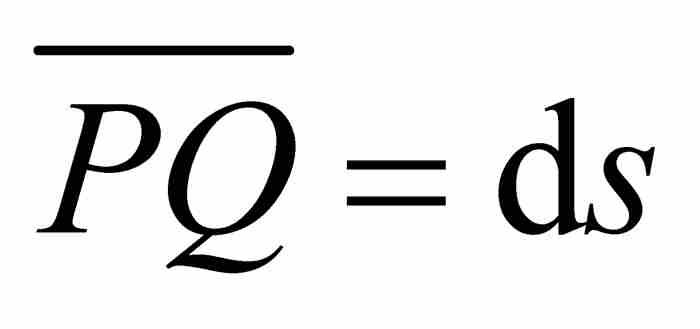 ,高為
,高為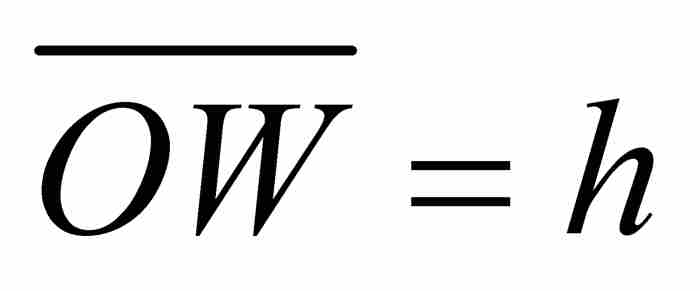 ,由此看出它的面積為
,由此看出它的面積為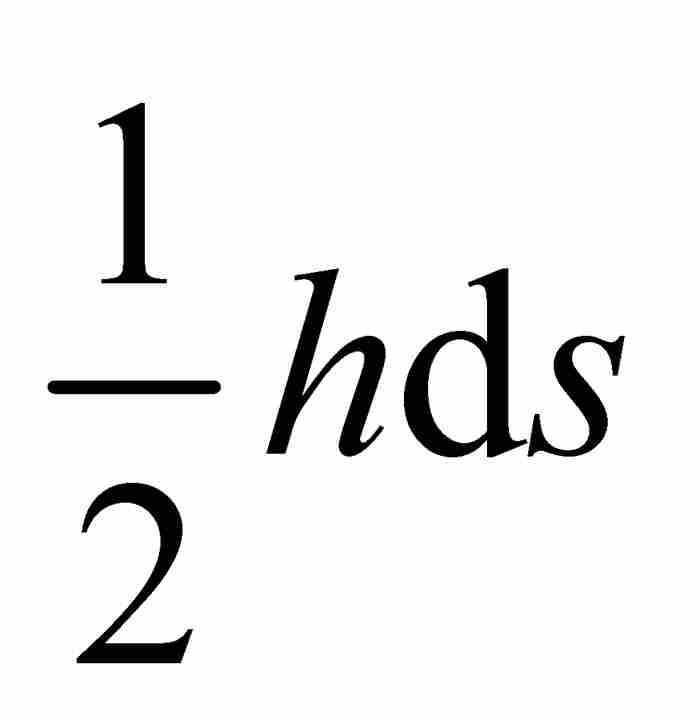 ,由上面的式(2)可知,這個面積恰好是
,由上面的式(2)可知,這個面積恰好是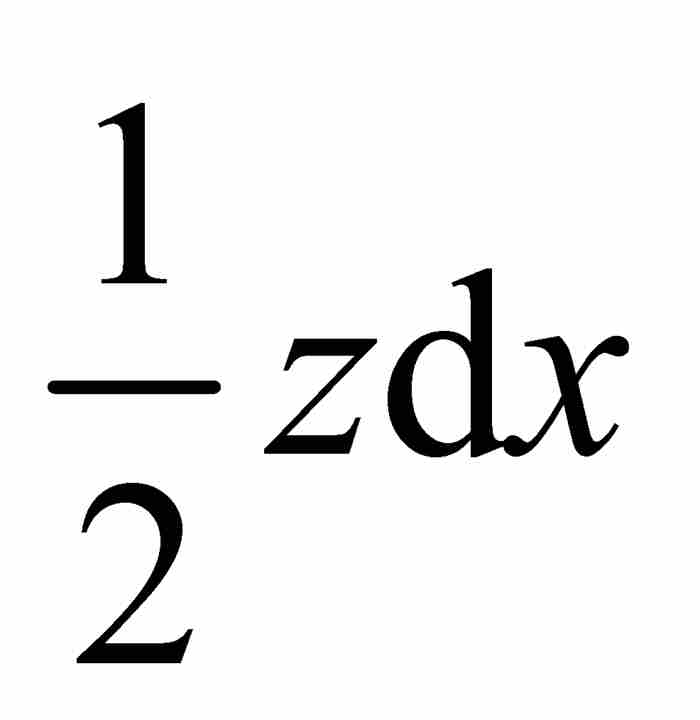 。
。
萊布尼茨畫了無數個這樣的無限小三角形,如圖2-5所示,所有的三角形都是從原點輻射出來並終止於曲線AB。幾年以後,萊布尼茨回憶起,他「偶然有機會用若干條通過同一點的直線將面積分成多個三角形,並且……察覺可以很容易從中獲得某些結果」。4
4 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 42。
這種極透視三角形是非常關鍵的,因為萊布尼茨認識到圖2-5中的楔形的面積就是那些無窮小三角形的面積之和,它們的面積的解析表達式已經在上面確定。就是說
面積(楔形)=三角形面積之和=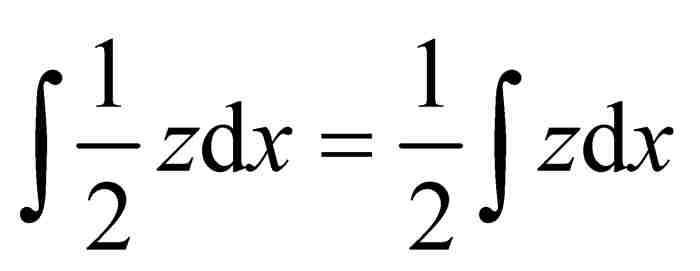 (3)
(3)
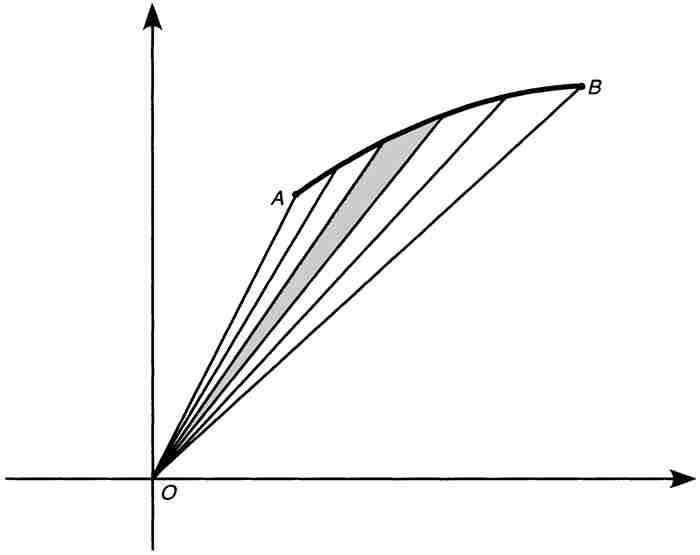
圖 2-5
事實上,萊布尼茨的初衷並不是求這個楔形的面積。相反,他要尋求的是圖2-1中曲線AB之下的面積,即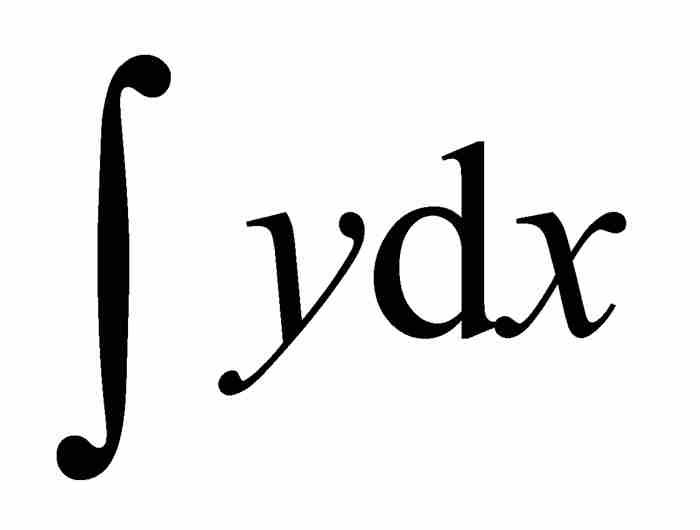 。幸好,只需要簡單地修修補補就可以將討論中的兩個面積聯繫起來。圖2-6中的幾何圖形表明:
。幸好,只需要簡單地修修補補就可以將討論中的兩個面積聯繫起來。圖2-6中的幾何圖形表明:
曲線AB下的面積=面積(楔形)+面積(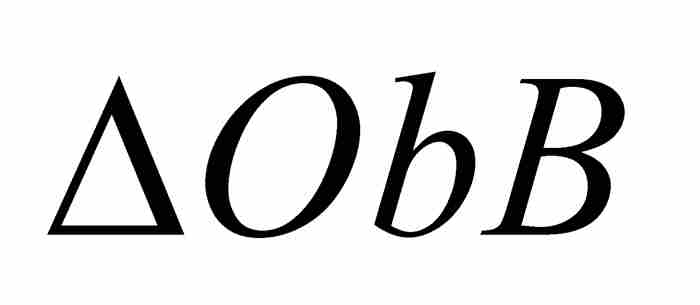 )-面積(
)-面積( )
)
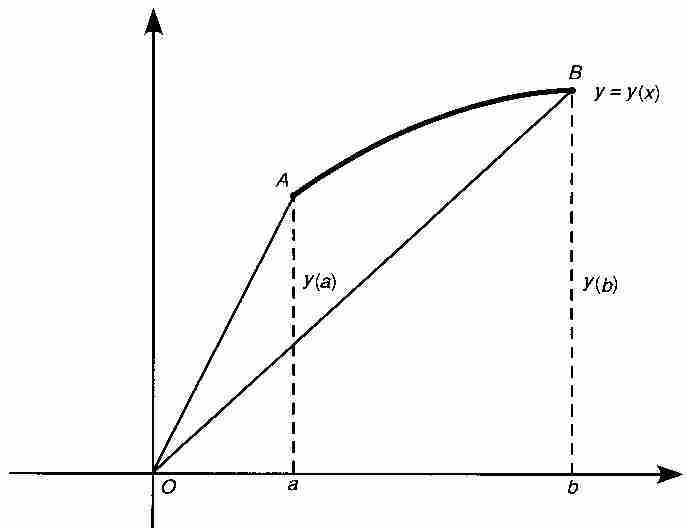
圖 2-6
根據式(3),這個關係式從符號上等價於
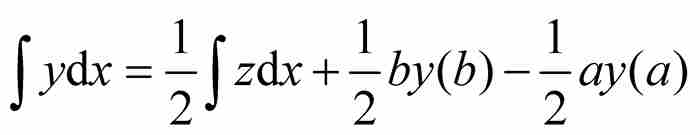 (4)
(4)
這就是最終的變換定理。定理的名稱表示原來的積分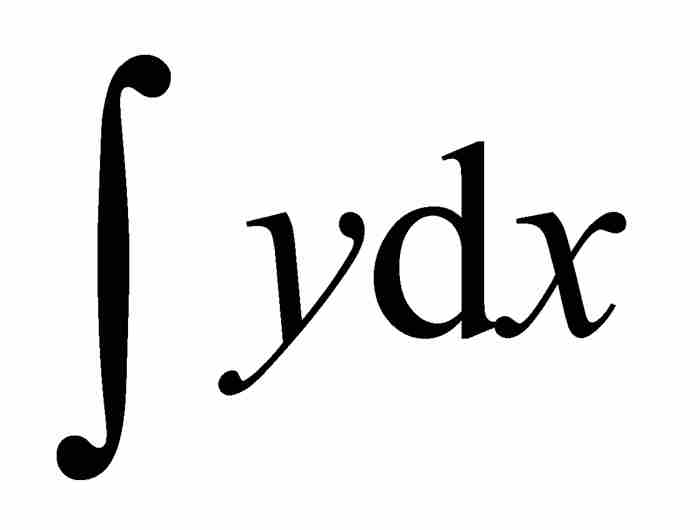 已經變換(或「轉換」)成新積分
已經變換(或「轉換」)成新積分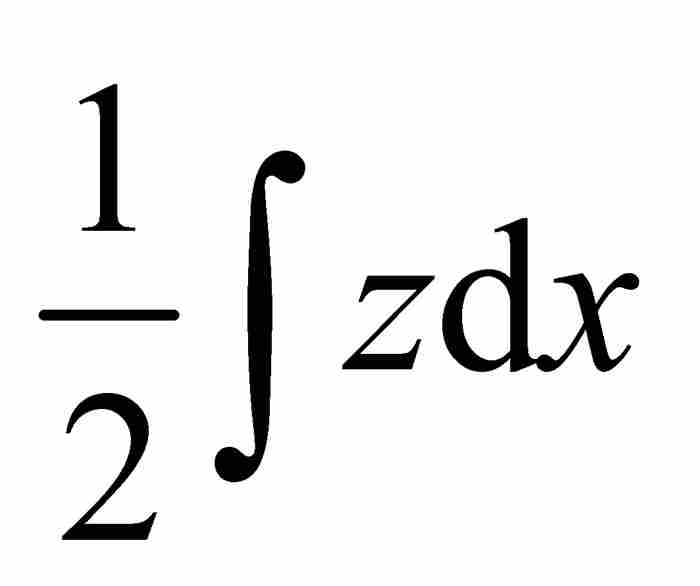 與常數
與常數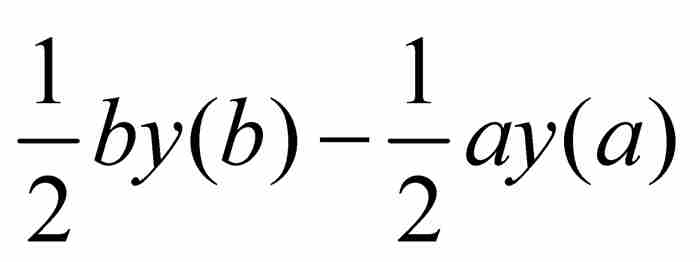 之和。如今,我們添加積分限(一個萊布尼茨沒有用過的符號表示法)使得公式更稱心如意,並且重寫成
之和。如今,我們添加積分限(一個萊布尼茨沒有用過的符號表示法)使得公式更稱心如意,並且重寫成
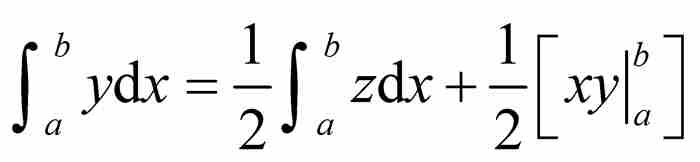 (5)
(5)
公式(5)由於至少以下兩個原因而值得注意。
首先,「新的」對 z 的積分很可能比原來對 y 的積分更容易求值。如果是這樣,z 就在求原來的面積中扮演了一個輔助的角色。對17世紀的數學家來說,一種稱為割圓曲線的曲線就扮演這樣的角色,也就是說,割圓曲線是一個求面積的助推器。如果從公式(5)能夠產生一個更簡單的積分,那麼,這整個冗長的推導過程將獲得補償。正如我們立刻就會看到的,這種情況恰好出現在萊布尼茨級數的推導過程中。
其次,公式(5)中的關係具有理論意義。回想一下,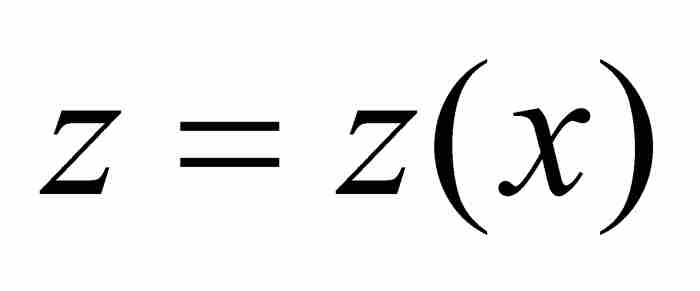 是曲線AB在點(x, y)處的切線在y軸的截距。因此 z 的值與切線的斜率有關,所以在這個復合的積分中注入了導數。這不禁使人意識到其中隱藏著重要的聯繫。
是曲線AB在點(x, y)處的切線在y軸的截距。因此 z 的值與切線的斜率有關,所以在這個復合的積分中注入了導數。這不禁使人意識到其中隱藏著重要的聯繫。
為更清楚地看到這一點,回想式(1)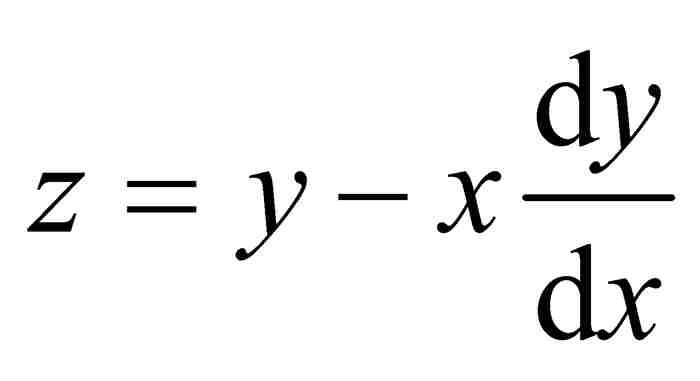 ,可得
,可得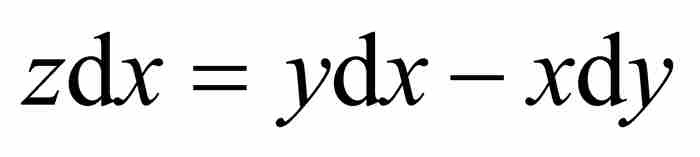 。代入式(4)得到
。代入式(4)得到
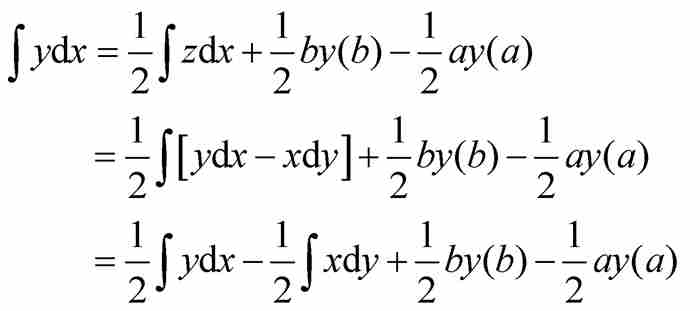
求解得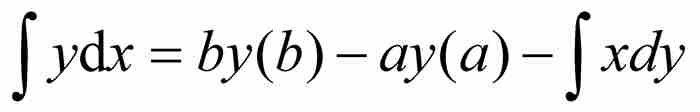 。
。
再加入積分限,給出
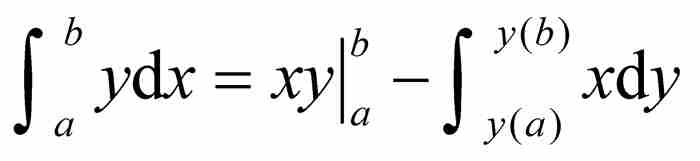 (6)
(6)
在圖2-7中,式(6)在幾何上的正確性是顯而易見的,因為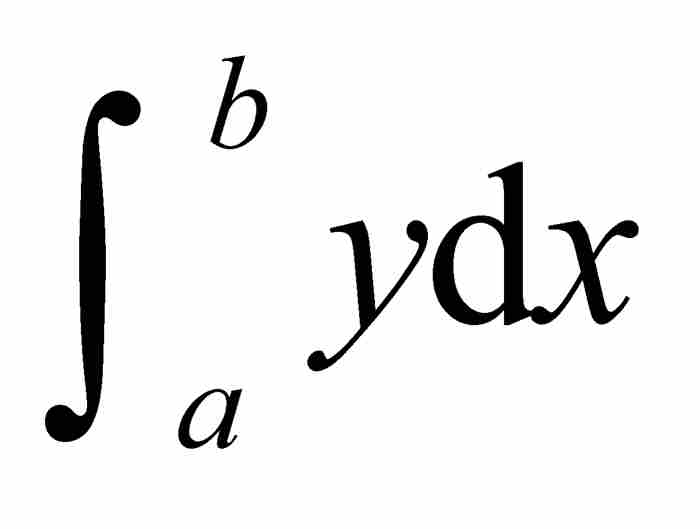 是所有縱向條形區域的面積,而
是所有縱向條形區域的面積,而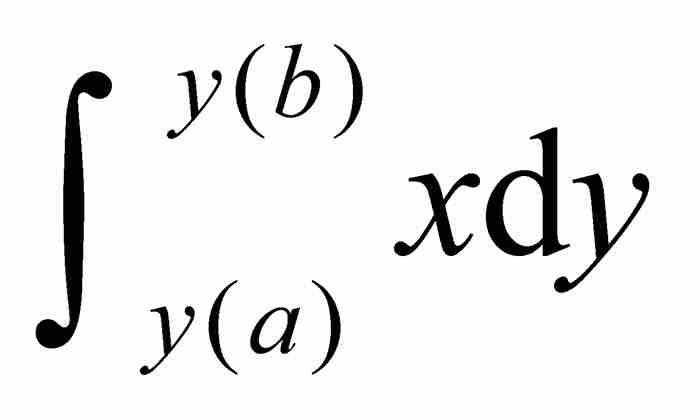 是所有橫向條形區域的面積。這兩部分面積的和顯然是外圍矩形和左下方小矩形面積之差。就是說,
是所有橫向條形區域的面積。這兩部分面積的和顯然是外圍矩形和左下方小矩形面積之差。就是說,
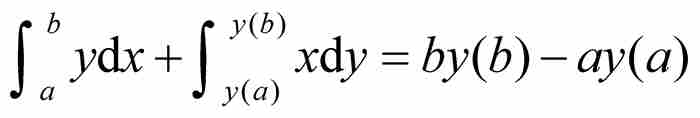
整理後即得式(6)。
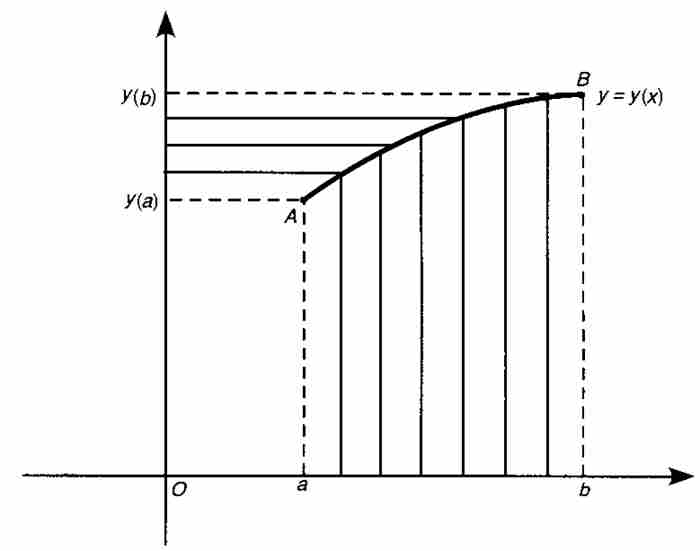
圖 2-7
關於式(6)還要作一點說明:它看起來是大家熟悉的。這是理所當然的,因為它很容易地從著名的分部積分法公式
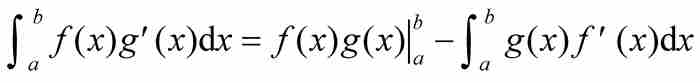
推出,只要在其中指定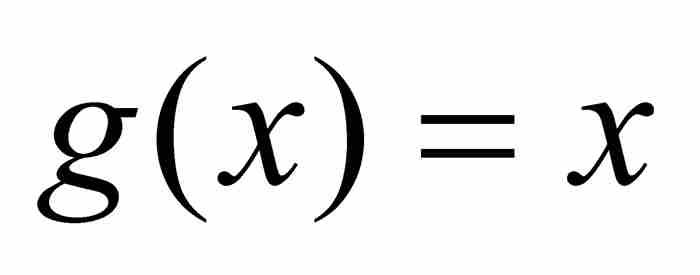 和
和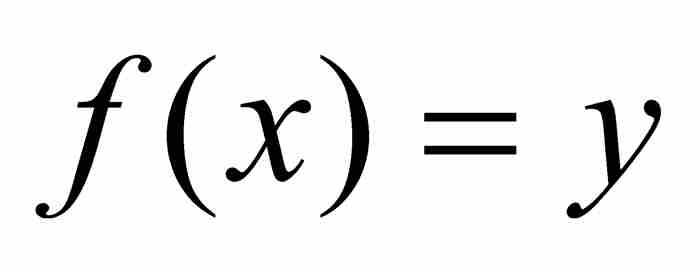 。在這種條件下
。在這種條件下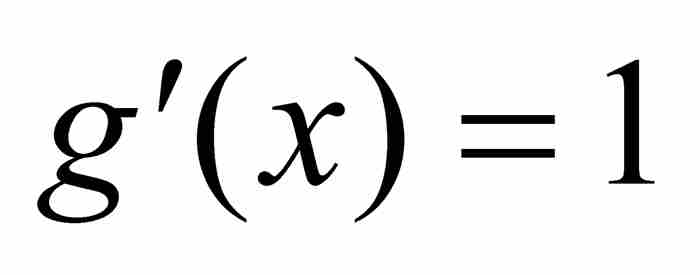 ,
,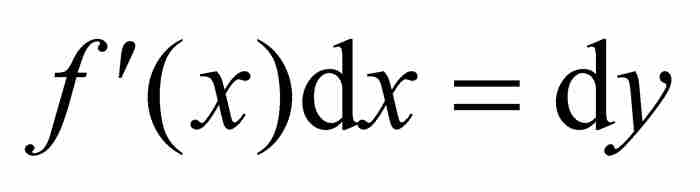 ,代入後就把分部積分公式轉變成變換定理。萊布尼茨在使用無限小三角形、切線、相似三角形和楔形面積進行複雜推理以後,總之,在經過極其曲折的數學探索之旅以後,獲得一個分部積分的實例,一位微積分的超級明星捷足先登,出人意料地走上舞台。
,代入後就把分部積分公式轉變成變換定理。萊布尼茨在使用無限小三角形、切線、相似三角形和楔形面積進行複雜推理以後,總之,在經過極其曲折的數學探索之旅以後,獲得一個分部積分的實例,一位微積分的超級明星捷足先登,出人意料地走上舞台。
這是令人興奮的,但是萊布尼茨並沒有停下腳步。在把他的變換定理應用於一條著名的曲線後,萊布尼茨發現了一個一直以他的名字命名的無窮級數。
萊布尼茨級數
萊布尼茨從一段圓弧開始。他特別考察半徑為1和中心在點(1, 0)的圓,如圖2-8所示。他把這個圓的四分之一作為他的一般變換定理裡的曲線AB。下面馬上就會看到,這是一個富有靈感的選擇。
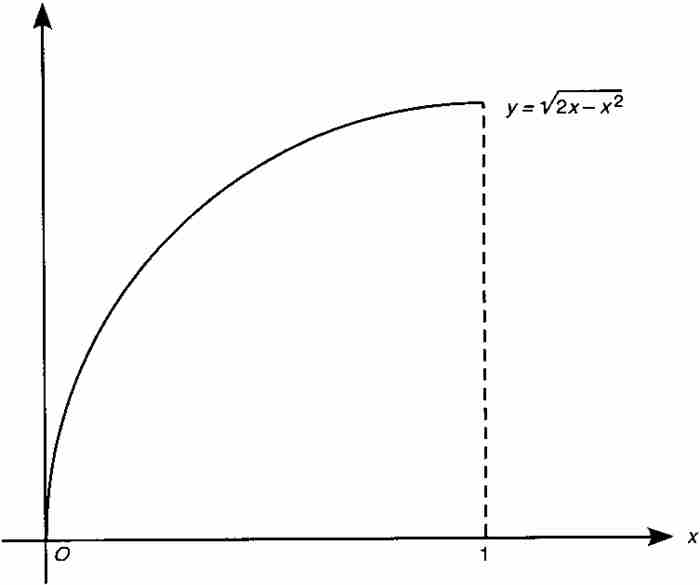
圖 2-8
圓的方程為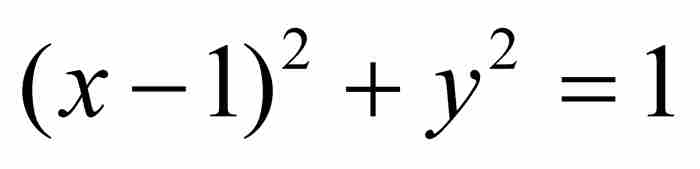 ,或者取另一種形式
,或者取另一種形式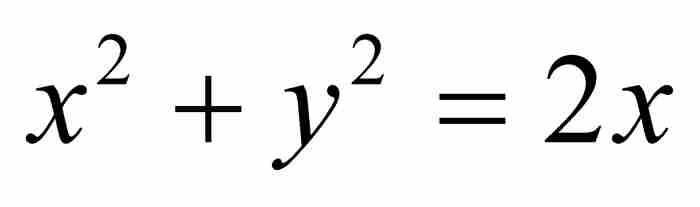 。由幾何圖形可知這段四分之一圓弧下的面積是
。由幾何圖形可知這段四分之一圓弧下的面積是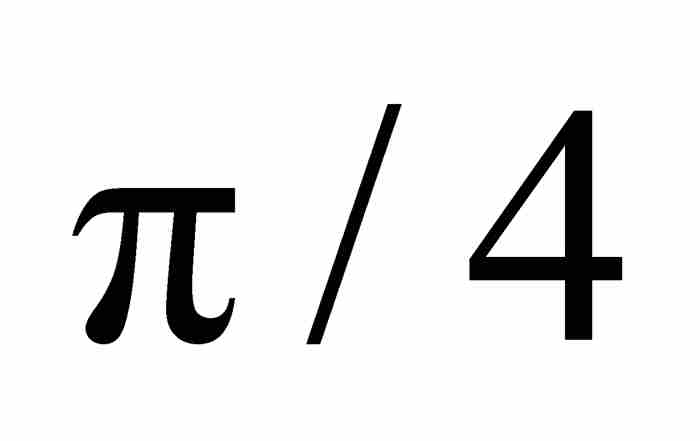 ,所以由式(1)和式(5)可得
,所以由式(1)和式(5)可得
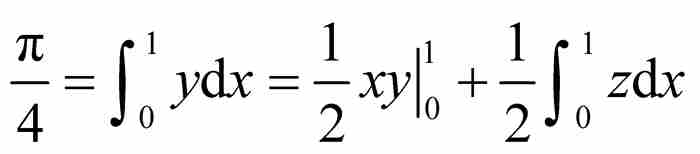 ,其中
,其中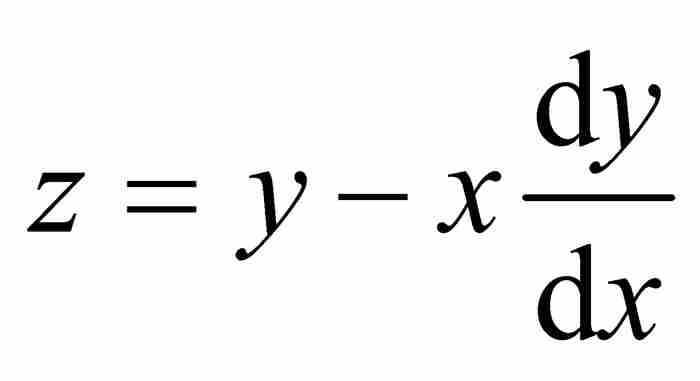
菜布尼茨利用他新創建的積分,對圓的方程求微分,得到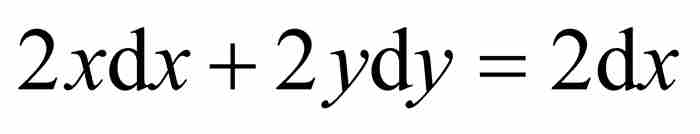 ,於是
,於是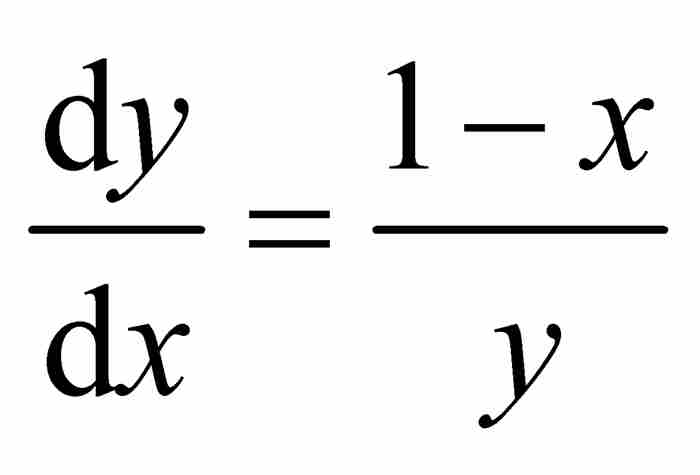 。這使式(1)簡化成
。這使式(1)簡化成
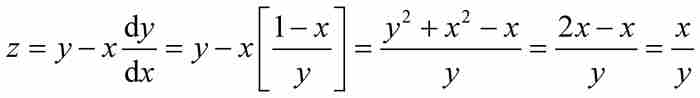
萊布尼茨的目標是求得由割圓曲線z的項來表示x的表達式,因此他將上式平方並利用圓的方程,得到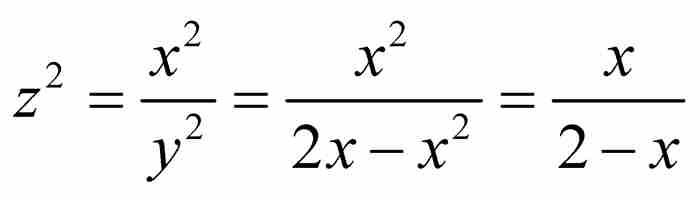 ,從中解出
,從中解出
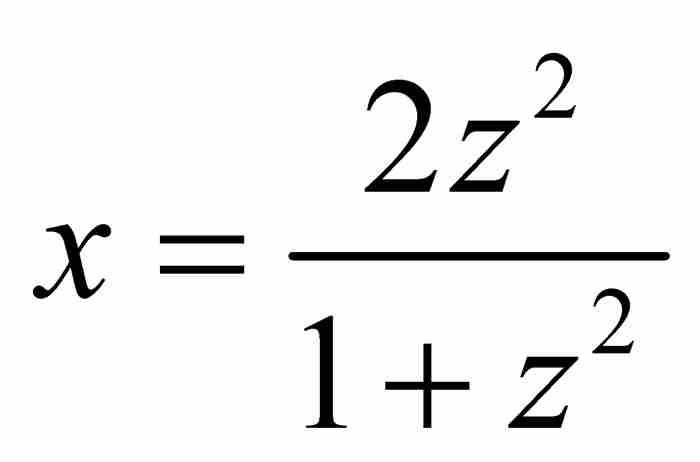 (7)
(7)
挑戰在於計算圖2-9中陰影區域的面積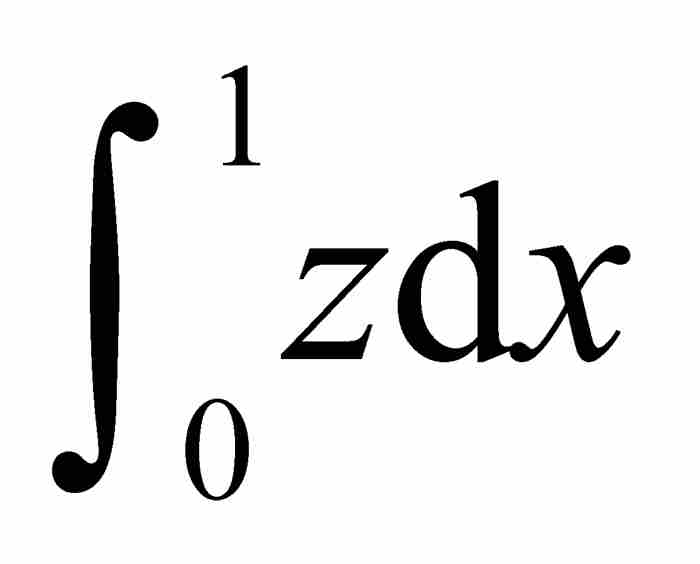 。考慮割圓曲線
。考慮割圓曲線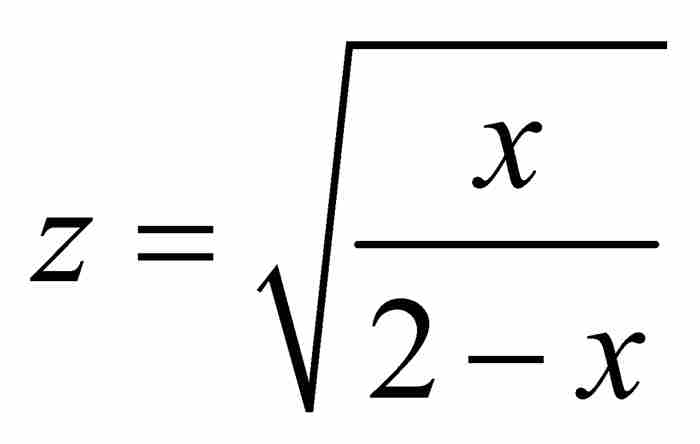 的圖形,並按上述推導過程,證實
的圖形,並按上述推導過程,證實
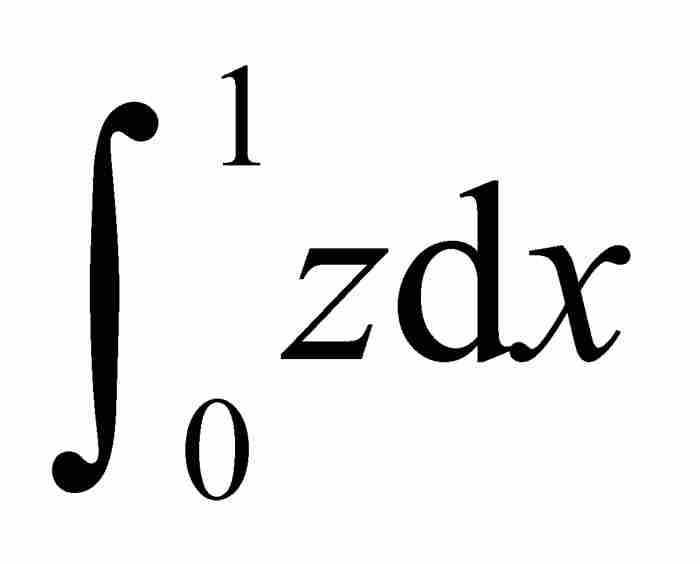 =面積(陰影區域)
=面積(陰影區域)
=面積(正方形)-面積(上方區域)=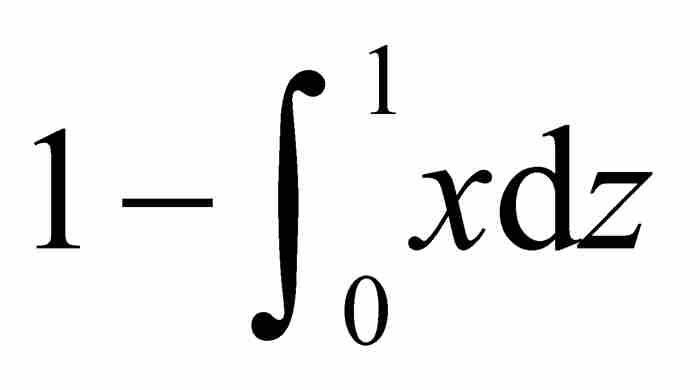 (8)
(8)
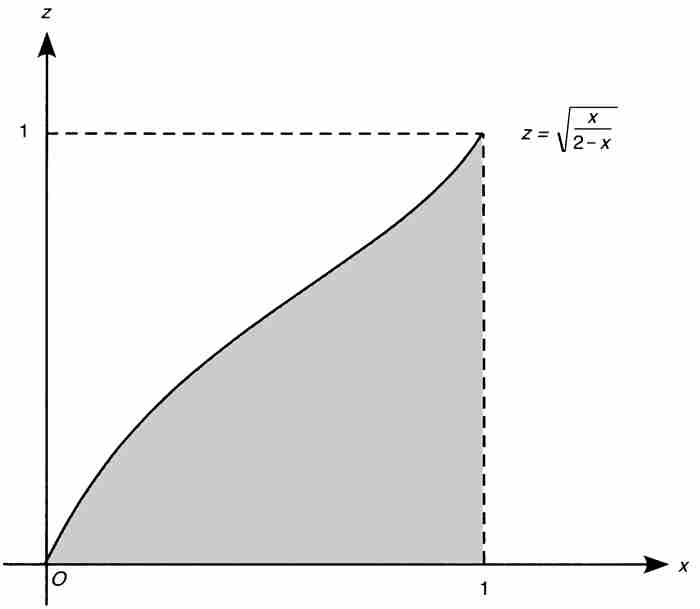
圖 2-9
回到變換定理,萊布尼茨把式(7)和式(8)結合起來,得到
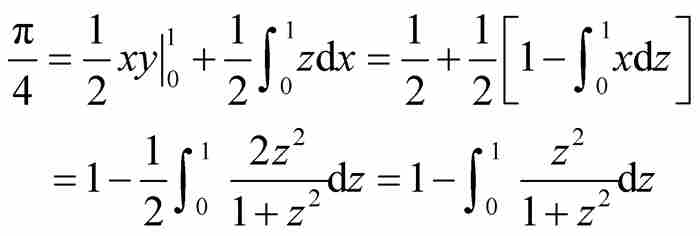
他將最後的被積函數重寫成
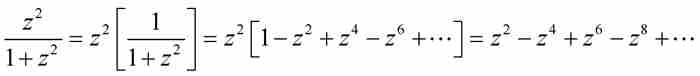
其中方括號內出現了一個等比級數。據此,萊布尼茨推斷
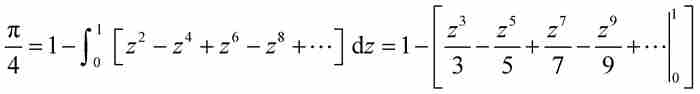
化簡成
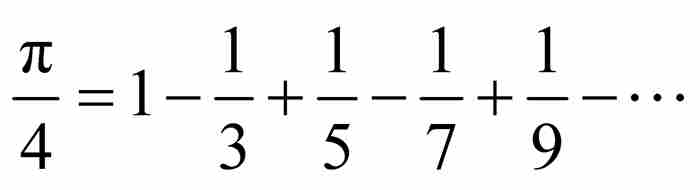 (9)
(9)
這就是萊布尼茨級數。
這是一個奇妙的級數。它的項遵循一個極為普通的模式:帶有交替正負號的奇數的倒數。然而最重要的是,這個看似不起眼的表達式的和為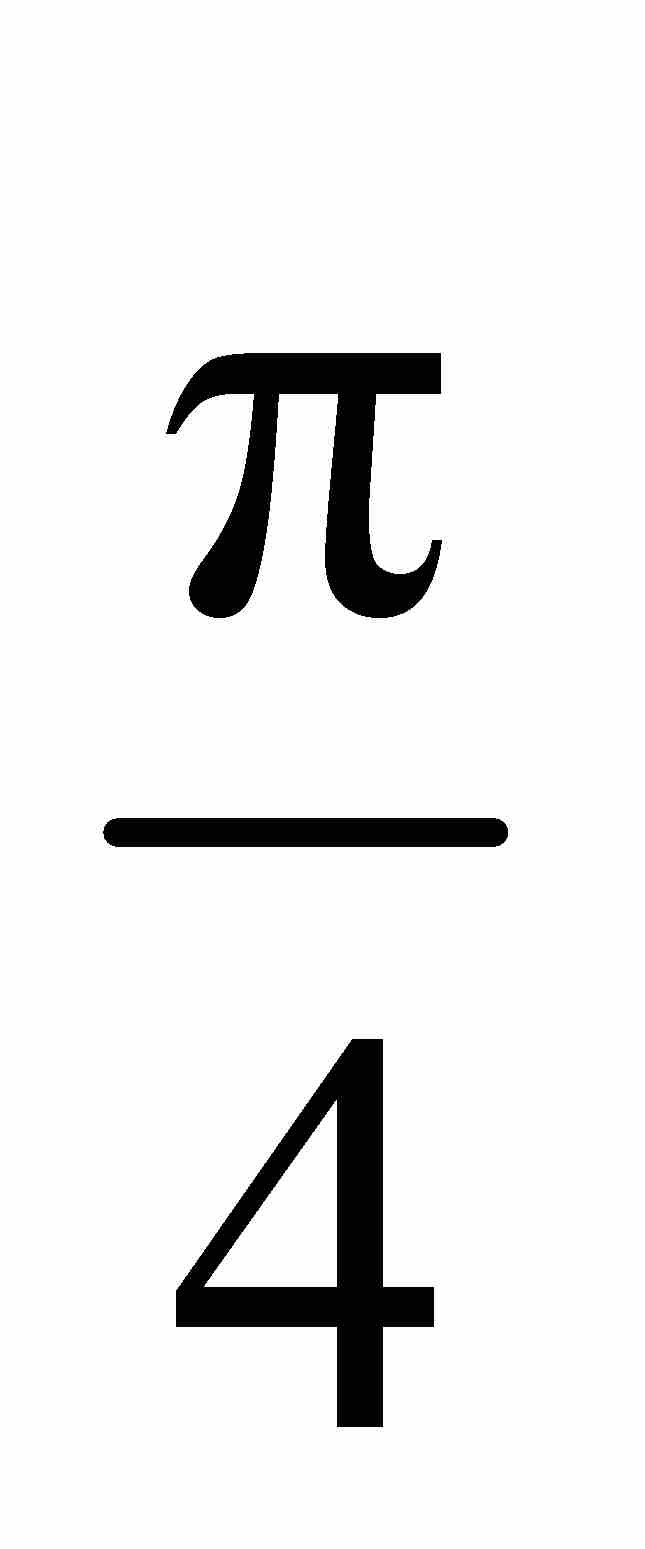 。萊布尼茨回憶當他第一次將這個結果同惠更斯交流時,他得到熱烈的讚揚,因為「惠更斯給予了極高的評價,並且在退回這篇論文的附信中說,這在數學家中是一個值得永遠記住的發現」。1
。萊布尼茨回憶當他第一次將這個結果同惠更斯交流時,他得到熱烈的讚揚,因為「惠更斯給予了極高的評價,並且在退回這篇論文的附信中說,這在數學家中是一個值得永遠記住的發現」。1
1 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 46。
按照萊布尼茨的說法,這個發現的意義在於「第一次證明了圓的面積恰好等於有理數的一個級數」。2 也許有人會對他用「恰好」一詞挑毛病,但是很難同他的熱情爭辯。
2 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 47。
他追加了一個離奇的補遺。通過對式(9)兩端除2,並組合其中的項,萊布尼茨發現
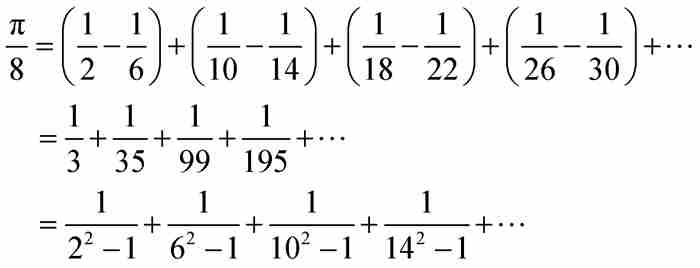
就是說,這個等式表明,如果我們從2開始對每個相間的偶數的平方減1的倒數求和,結果為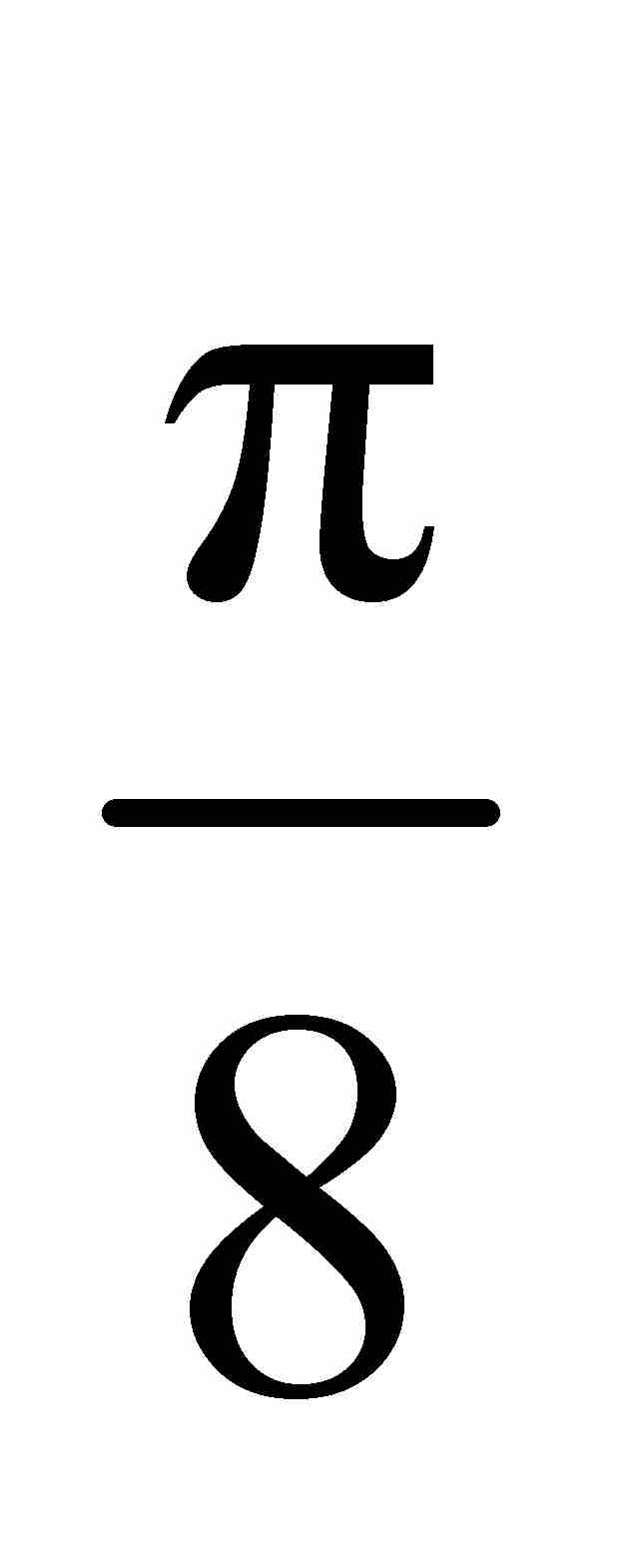 。多麼神奇!這提醒人們,分析學家手中的公式近乎魔術一般。
。多麼神奇!這提醒人們,分析學家手中的公式近乎魔術一般。
萊布尼茨級數在形式上是著名的,但如果用它計算π的近似值則毫無價值。這個級數是收斂的,不過收斂極為緩慢。如果對萊布尼茨級數的前300項求和,僅能得到π的精確到一位小數的近似值。這麼糟糕的精度是不值得費力地去求和的。但是,我們將會看到,在歐拉手中,一個相關的無窮級數將產生一個高效的計算π的近似值的方法。
毫無疑問,萊布尼茨級數是一個微積分學的傑作。然而,按照慣例,當討論這些早期的結果時,我們必須提出一些注意事項。值得一提的第一件事,是變換定理使用了無窮小推理。另一件事,是萊布尼茨在求其級數的值時需要用無限多積分項之和代替無限多項之和的積分,這樣一個步驟,它的微妙性將成為未來幾個世紀面對的問題。
同時,還有另外一個問題:萊布尼茨並不是第一個發現這個級數的人。英國數學家詹姆斯·格雷戈裡在其幾年前已經發現一個非常相似的級數。事實上,格雷戈裡得到了反正切函數的展開式,即
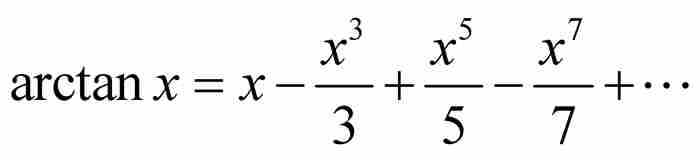
當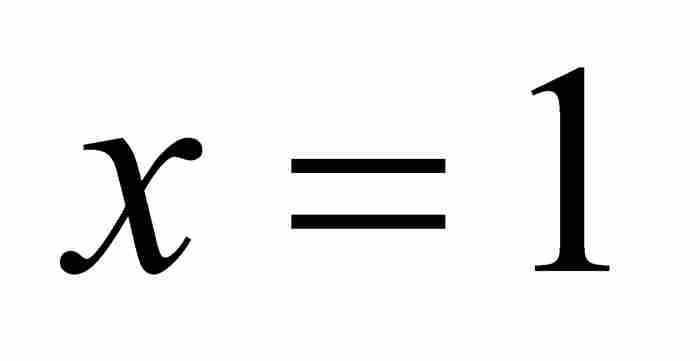 時,這就是萊布尼茨級數(雖然格雷戈裡也許實際上並未作過代換,沒有將這個函數級數轉換成數值級數)。
時,這就是萊布尼茨級數(雖然格雷戈裡也許實際上並未作過代換,沒有將這個函數級數轉換成數值級數)。
在1674年,作為數學新手的萊布尼茨並不知道格雷戈裡的成果,並相信他自己找到了新東西。這反過來讓他的英國對手對他投以懷疑的目光。對他們來說,萊布尼茨具有攫取他人成果的傾向。這些懷疑在18世紀初期自然會被進一步放大,因為那時在牛頓親自指揮下,整個英國都在指責萊布尼茨剽竊微積分的抄襲行為。級數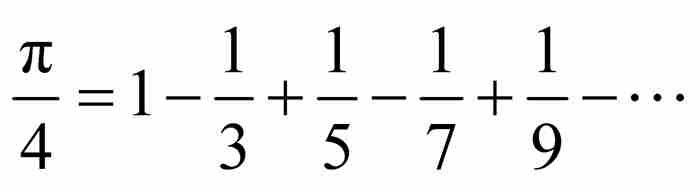 中的這筆糊塗賬被當作是萊布尼茨背信棄義的最初例證。
中的這筆糊塗賬被當作是萊布尼茨背信棄義的最初例證。
但是,即使是格雷戈裡也不是第一個涉足這條道路的人。我們在前一章中提到的印度數學家尼拉坎塔在一本名為Tantrasangraha的書中描述了這個級數,還是用韻文的形式。3 雖然這一成果在萊布尼茨時代的歐洲尚不為人知,但這件事提醒世人,數學是全人類的事業。
3 Ranjan Roy, 「The Discovery for the Series Formula for π by Leibniz, Gregory and Nilakanta, 」 Mathematics Magazine, vol. 63(1990),no. 5, pp. 291-306。
儘管有格雷戈裡和尼拉坎塔的成果,但是我們知道萊布尼茨的級數推導不是剽竊行為。後來他在1674年寫道,不論是他還是惠更斯「或者任何一個在巴黎的其他人,完全沒有聽說過任何關於通過有理數的無窮級數表示圓面積的報道」。4 像發明通常的微積分一樣,萊布尼茨級數是一項屬於個人的成就。
4 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 46。
在接下來的20多年裡,當萊布尼茨完善、整理並且發表了他關於微分學和積分學的思想後,這個新手變成為一位大師。在這樣的起點上,這門學科將在未來的一個世紀發展起來——事實上將迅猛地成長s。我們將繼續講述這個故事,談談他在瑞士的兩位最著名的追隨者,即伯努利兄弟二人。
