20世紀傑出的數學家約翰·馮·諾伊曼（1903—1957）在論述微積分時寫道：「微積分是現代數學取得的最高成就，對它的重要性怎樣估計也是不會過分的。」1
1 John von Neumann, Collected Works, vol.1, Pergamon Press, 1961, p.3。
今天，在微積分出現3個多世紀之後，它依然值得我們這樣讚美。微積分儼如一座橋樑，它使學生們通過它從基礎性的初等數學走向富於挑戰性的高等數學，並且面對令人眼花繚亂的轉換，從有限量轉向無限量，從離散性轉向連續性，從膚淺的表象轉向深刻的本質。所以，英語中通常在微積分一詞calculus前面鄭重地加上定冠詞「the」，馮·諾伊曼在上述評價中就是這樣做的。「the calculus」（微積分）這種稱謂同「the law」（定律）相似，用「the」特指微積分是一個浩如煙海的、獨立存在且令人敬畏的科目。
一如任何重要的智力探索過程，微積分有著五彩斑斕的發展史和光怪陸離的史前史。西西里島錫拉丘茲城的阿基米德（大約公元前287—公元前212）曾用我們現在所知的一種最早的方法求出某些幾何圖形的面積、體積和表面積。在漫長的800餘年後，法國數學家皮埃爾·德·費馬（1601—1665）採用一種非常現代的方法確定了曲線的切線斜率和曲線下面區域的面積。他們以及其他許許多多著名的前輩數學家們把微積分推上了歷史舞台。
不過，這不是一本描寫數學先驅們的書。不言而喻，微積分在很大程度上應歸功於以往的數學家，恰如現代藝術在很大程度上應歸功於過去的藝術家一樣。但是，一座專題博物館——例如現代藝術博物館——並不需要用一間又一間陳列室去展覽對後世有影響的前現代藝術作品。就是說，這樣一種博物館的展覽可以從中期開始。所以，對於展示微積分創建的歷程，我想也可以這樣做。
因此，我將從17世紀的兩位學者艾薩克·牛頓（1642—1727）和戈特弗裡德·威廉·萊布尼茨（1646—1716）開始，正是他們兩人促成了微積分的降生。萊布尼茨在1684年的一篇論文中率先發表了他的研究成果，文章的標題中包含一個拉丁詞calculi（一種計算系統），這個詞後來就用來指代這門新生的數學分支。第一本教科書在十幾年之後面世，微積分（the calculus）的名稱在書中被確定下來。
其後幾十年，其他幾位數學家先承接了挑戰。在這些先驅者中，最傑出的人物當推雅各布·伯努利（1654—1705）和約翰·伯努利（1667—1748）兄弟二人，以及舉世無雙的萊昂哈德·歐拉（1707—1783）。在他們的研究成果中有成千上萬的頁面涉及最高品位的數學，研究範圍擴展到包羅極限、導數、積分、無窮序列、無窮級數以及其他許許多多主題在內的各個方面。這個四處延伸的題材帶有一個稱為「分析學」的總標題。
由於複雜性的日益增加，有關基本邏輯的各種困難問題也接踵而至。儘管微積分強大有力又具有實用價值，但是它建立在一種不牢靠的基礎之上。這使數學家們認識到，需要按照歐幾里得幾何的模型，採用一種精確和嚴格的方式重建這門學科。這樣一項緊迫的任務是由19世紀的分析學家奧古斯丁·路易·柯西（1789—1857）、格奧爾格·弗雷德裡希·貝爾哈德·黎曼（1826—1866）、約瑟夫·劉維爾（1809—1882）和卡爾·魏爾斯特拉斯（1815—1897）完成的。這幾位數學大師以前所未有的熱忱工作著，他們不辭艱辛，確切地定義了所用的術語，並且一一證明了到那時為止被數學界毫無爭議地接受的各種結果。
但是，一些問題的解決，推開了另外一些問題的大門——這是在科學發展中經常發生的事情。在19世紀下半葉，數學家們利用這些邏輯上嚴密的工具構造出大量奇特的反例，對它們的認識讓分析學具有了空前的普遍性和抽像性。我們從格奧爾格·康托爾（1845—1918）的集合論以及後來的維托·沃爾泰拉（1860—1940）、勒內·貝爾（1874—1932）和亨利·勒貝格（1875—1941）等學者的成就中，可以明顯看出這種趨勢。
到20世紀初，分析學已經匯聚成包含無數概念、定義、定理和實例的一座寶庫——並且發展為一種獨具特色的思維方式，因此確立了它作為一個至高無上的數學體系的地位。
我們要從這座寶庫中取出一批樣品，目的是考察上面提到的那些數學家獲得的成果，並且以一種忠實於原貌同時又讓當今讀者能夠理解的方式展現出來。我將探討那些能夠說明微積分在其形成年代的發展狀況的定理，認識那些最卓越的天才創建者們。簡言之，本書是一部翻開這段令人神往的歷史的「重要定理」集。
為了達到這個目標，我僅限於介紹少數有代表性的數學家的工作。首先我要坦誠披露：對於人物的安排是由本人的鑒賞傾向決定的。本書收入像牛頓、柯西和魏爾斯特拉斯這樣一些數學家，他們會出現在任何一本類似的書中。選入另外一些數學家，如劉維爾、沃爾泰拉和貝爾等人，更多地是出於我個人的喜好。至於其他一些數學家，如高斯、波爾查諾和阿貝爾，他們則不在我的考慮之列。
同樣，我討論的某些定理是數學文獻的所有讀者都熟知的，儘管它們原有的證明對於不精通數學史的人而言是離奇的。萊布尼茨1673年關於「萊布尼茨級數」幾乎不被人們承認的推導，以及康托爾1874年關於連續統不可數性的鮮為人知的首次證明，就屬於這種情況。另外一些定理雖然在數學上是司空見慣的，但是很少出現在現代教科書中——這裡我所指的是像魏爾斯特拉斯構造的處處連續而無處可微的函數的結果，當他在1872年把這個結果提交給柏林科學院時引起了數學界的震驚。至於我的某些選擇，我承認，是十分怪異的。例如書中包含歐拉對積分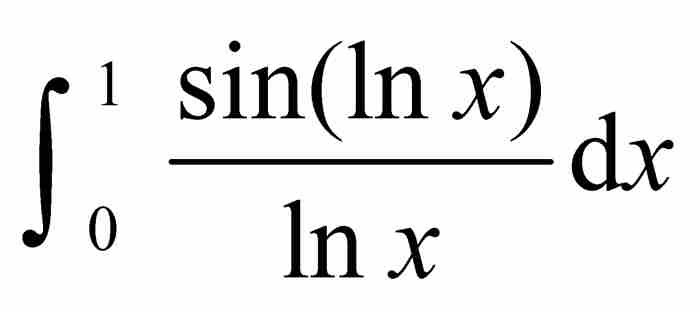
的估值，這不過是為了展現這位數學家在分析學方面的奇才。
書中的每一個結果，從牛頓的正弦級數的推導，到伽瑪函數的表示，再到貝爾的分類定理，都處於所在時代的研究前沿。總的說來，它們記錄了分析學隨著時間的演進過程，以及參與者們在風格上和實質上的變化。這種演進是引人矚目的，因為可以將勒貝格1904年的一個定理同萊布尼茨1690年的一個定理之間的差別，比擬為現代文學同英國古典英雄史詩《貝奧武甫》之間的區別。儘管如此，我仍然相信每個定理都顯示出值得我們關注甚至讚美的獨創性——這一點是至關重要的。
自然，打算憑借考察幾個定理來刻畫分析學的特徵，猶如試圖通過採集幾點雨滴來描繪一場雷雨的特徵，所表達的觀念不可能全面。為了擔負這樣一項任務，作者必須採納某些恰當的限製作為準則。
我的準則之一是避免貪大求全，去寫一部描寫分析學發展進程的全面的歷史書。無論如何，這是一項過於宏大的任務，何況已經出版了許多論述微積分發展的著作。我所喜愛的一些書籍已在正文中明確提出，或者作為資料列入參考文獻。
第二條準則是把多元微積分和復分析排除在外。這樣做或許是一種令人遺憾的選擇，不過我相信是正確的。據此把這本書的內容被置於某種可以控制的範圍內，從而增添敘述的連貫性。此種限制同時把對讀者背景的要求降低到最低程度，因為一本只討論一元實分析的書，能夠理解它的讀者將是最廣泛的。
這就提出預備知識的問題。針對本書面對的讀者，我寫進許多技術細節，所以只要具備最基本的數學知識就能理解書中的定理。某些早期的結果要求讀者有毅力看完不止一頁的代數運算。至於後期的某些結果則需要純粹抽像的判別能力。一般而言，我不會對數學上缺乏勇氣的人推薦此書。
同時，為力求達到簡明扼要，同一本標準的教科書不同，我採用比較隨意的寫法。我的本意是想讓這本書對於那些或多或少具備大學數學程度的讀者，或者那些沒有被隨處可見的積分或ε符號嚇倒的讀者來說，更容易接受。我的目標是使預備知識剛好夠用於理解所述主題，但是又不能再少。要是不這樣做，將會使內容索然寡味，無法達到我的更大目標。
所以說這首先不是一本數學家的傳記，也不是一部微積分的歷史，更不是一冊教科書。事實上，儘管在書中我有時記述傳記材料，有時探討某個主題同另一個主題之間的聯繫的歷史，而且有時也採用教科書的方式介紹新奇的（或者久已被遺忘的）概念，我仍要指出這一點。不過我最初的動機是很簡單的：同讀者分享分析學的豐富歷史中為人們喜聞樂見的某些結果。
同時，這引起我作最後一點說明。
在多數學科中存在著一種傳統，那就是研究卓越的先驅們的主要著作，那些先驅乃是學科領域中被稱為「大師」的傑出人物。學文學的學生要拜讀詩人和劇作家莎士比亞的作品；習音樂的學生需聆聽作曲家巴赫的樂曲。然而在數學界，如果說這樣一種傳統不是完全沒有的話，那麼至少也是非常罕見的。本書是想使這種局面得以改觀。不過我不打算把它寫成一部微積分的歷史，而必須把它作為展示微積分宏偉畫卷的陳列室。
為了這一目的，我彙集了若干傑作，只不過它們不是繪畫大師倫勃朗或者凡高創作的油畫，而是歐拉或者黎曼證明的定理。這樣一座陳列室或許有一些獨特之處，但是它的目標同一切有價值的博物館一樣：成為一座優異的知識寶庫。
像任何陳列室一樣，這座陳列室的藏品中仍然存在空白。也像任何陳列室一樣，這座陳列室不可能為人們希望展出的所有收藏品提供足夠的空間。雖說有這些局限性，但是當一位參觀者離去時，他必然會對天才人物們充滿感激之情。同時，那些徜徉於展品之間的人們將從最終的分析學中體驗到數學中最深奧的想像力。