
通常,一場科學革命不單是需要一位奠基的天才。它往往也需要一位組織天才,去確立科學中的核心思想,對它的產物去粗取精,去偽存真,並使之能為大眾理解。一位卓越的建築設計師可以設計出一幅宏偉的藍圖,但是這份藍圖終究需要一支建築隊伍將其變成一座大廈。
如果說牛頓和萊布尼茨是微積分的建築設計師,那麼正是雅各布·伯努利和約翰·伯努利所做的大量工作,才把微積分建立成今天我們所知的這門學科。這兄弟二人閱讀了萊布尼茨從1684年到1686年發表的最早論文,他們發現自己如臨決鬥前那樣興奮。他們抓住雲山霧罩般的闡述,充實它的細節,然後通過與萊布尼茨的交流以及兄弟彼此之間的交流,完善了統一性、條理性和術語。例如,「積分」一詞正是雅各布給出的。1 在他們手中,微積分變成當今學生易於接受的形式,即具有基本的求導法則、積分方法和初等微分方程的解法。
1 Howard Eves, An Introduction to the History of Mathematics, 5th Ed., Saunders College Publishing, 1983, p. 322。
雖然同屬優秀的數學家,但是伯努利兄弟二人的個人表現完全可以用「不得體」來形容。尤其是約翰,在萊布尼茨與牛頓關於微積分發明權之爭中充當了好鬥的角色,像萊布尼茨的牛頭犬一樣,忠實地站在他所尊奉為英雄的「大名鼎鼎的萊布尼茨」一邊,甚至聲稱牛頓不僅沒有發明微積分,而且從來沒有完全理解它。2 這當然是對歷史上最傑出的一個數學家的粗野無端的攻擊。
2 Richard S. Westfall, Never at Rest, Cambridge University Press, 1980, pp. 741-743。
非常不幸,由於家庭不和睦,雅各布和約翰也以相互爭鬥為樂。例如,哥哥雅各布稱弟弟約翰為「我的學生」,即使是在這個學生的才幹已經明顯和他相當的時候也是這樣。同樣,約翰在事隔多年後還在津津樂道地談論如何在一個晚上解決了困擾雅各布將近一年的一個問題。3
3 Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 473。
儘管他們具有難以相處的執拗天性,但是,伯努利兄弟還是在數學史上寫下了濃墨重彩的篇章。雅各布除了在微積分上的貢獻以外,還著有《猜度術》一書,在1713年(他去世後)出版。這本書是概率論的經典之作,書中給出大數定律的證明,為了紀念他,人們往往把這個基本結果稱為「伯努利定理」。4 至於約翰,他是世界上第一本微積分教科書的捉刀人。這件事情起於一項協議,按照協議約翰給法國貴族馬奎斯·德·洛必達(1661—1704)提供微積分課材料,獲取報酬。洛必達隨後在1696年整理出版了這些材料,書名為《用於瞭解曲線的無窮小分析》。在這本書裡首次出現「洛必達法則」,雖然同這本書一樣,這個法則實際上是約翰·伯努利發現的,但是這個名稱在微分學中從此就固定下來。5 在書的前言裡,洛必達表達了對伯努利和萊布尼茨的感謝,他寫道:「我無償地使用了他們的發現,所以只要他們願意,我真誠地把他們要求擁有的任何東西歸還他們。」6
4 Jakob Bernoulli, Ars conjectandi (Reprint), Impression anastaltigue, Culture et Civilisation, Bruxelles, 1968。
5 L'Hospital, Analyse des infiniment petits (Reprint), ACL-Editions, Paris, 1988, pp.145-146。
6 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard University Press, 1969, p. 312。
性情暴躁的約翰當然不滿足於這種表示,他確實聲明這個法則是他發明的,而在幾年後,他抱怨洛必達用金錢換取他人的才智。當然正如數學史家Dirk Struik所說,是伯努利自己(實際)促成了這起交易。他給我們的簡單的勸告是「就讓善良的馬奎斯持有他的典雅的法則吧,他支付費用了」。7 為避免再次失去榮譽,約翰寫了一篇關於積分學的內容廣泛的論文,在1742年用自己的署名發表。8
7 Dirk Struik, 「The origin of L'Hospital's rule,」 Mathematics Teacher, Vol. 56 (1963), p. 260。
8 Johannis Bernoulli, Opera omnia, vol. 3, Georg Olms, Hildesheim, 1968, pp. 385-563。
為更清楚瞭解伯努利兄弟二人在數學上的成就,我們有選擇地介紹他們的成果。首先從雅各布的調和級數的發散證明開始,然後考察他對一些奇異收斂級數的處理,最後介紹約翰對他所謂 「指數微積分」的貢獻。
雅各布和調和級數
像在他之前的牛頓和萊布尼茨以及許多後來的數學家一樣,雅各布·伯努利認為無窮級數是進入分析學的必由之路。這一點從1689年他所寫的專題論文《論無窮級數及其有限和》中可以明顯看出。這篇文章是對無窮級數的最高水平的討論,因為無窮級數在臨近17世紀末才被人們瞭解。1 雅各布考察了一類相似的級數,例如等比級數、二項式級數、反正切級數和對數級數,以及某些以前從未討論過的級數。在本章,我們考察從《論無窮級數及其有限和》中節錄的兩段文字,第一段專門討論調和級數的奇異特性。
1 「論無窮級數及其有限和」是雅各布·貝努利《猜度術》一書的附錄,參見[4],pp. 241-306。
在1689年之前很久,有人已經發現級數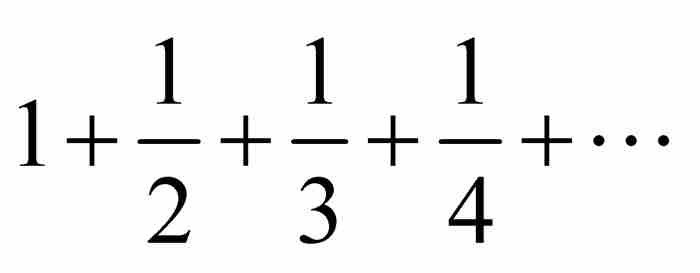 發散到無窮大。在大多數現代教科書中可以找到尼科爾·奧雷姆(大約1323—1382)發現的證明,以及彼得羅·門戈裡(1625—1686)提出的另一種證明。2 萊布尼茨也許並不瞭解這兩位先驅者的工作,在他早年在巴黎任職期間發現這個級數是發散的,用他的話說是
發散到無窮大。在大多數現代教科書中可以找到尼科爾·奧雷姆(大約1323—1382)發現的證明,以及彼得羅·門戈裡(1625—1686)提出的另一種證明。2 萊布尼茨也許並不瞭解這兩位先驅者的工作,在他早年在巴黎任職期間發現這個級數是發散的,用他的話說是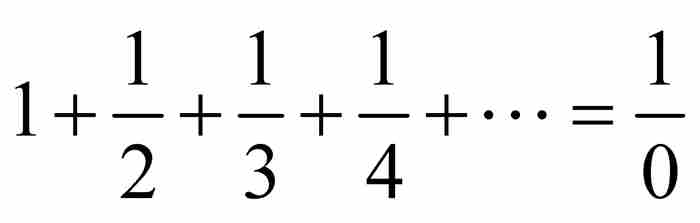 ,並告訴他的英國同行,而從他們那裡獲悉,又有人捷足先登了。3
,並告訴他的英國同行,而從他們那裡獲悉,又有人捷足先登了。3
2 參見William Dunham, Journey through Genius, Wiley, 1990, pp. 202-205。
3 Joseph E. Hofmann, Leibniz in Paris: 1672-1676, Cambridge Univesity Press, 1974, p. 33。
所以,調和級數的發散已不再是新聞。但是,我們通過下面另外一種方法得到同樣的結果,可以增長見識,更不必說其中的多樣性的魅力了。雅各布·伯努利的發散性證明就是與他的前輩們的證明迥然不同的這樣一種方法。
等比數列和等差數列在他那個時代如日中天,他首先從對比這兩類數列開始。他將前一種數列描述為A, B, C, D, …,其中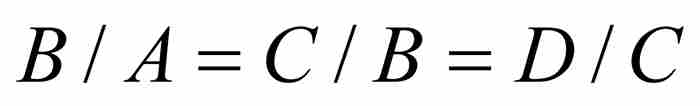 ,等等,例如,2, 1, 1/2, 1/4,…。他將後一種的數列,寫成A, B, C, D,…的形式,其中
,等等,例如,2, 1, 1/2, 1/4,…。他將後一種的數列,寫成A, B, C, D,…的形式,其中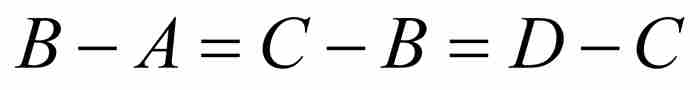 ,等等;一個例子就是2, 5, 8, 11,…。當然,現代的書寫習慣是強調等比數列的公比(r)和等差數列的公差(d),因此我們將等比數列寫成
,等等;一個例子就是2, 5, 8, 11,…。當然,現代的書寫習慣是強調等比數列的公比(r)和等差數列的公差(d),因此我們將等比數列寫成 ,
,  ,
, 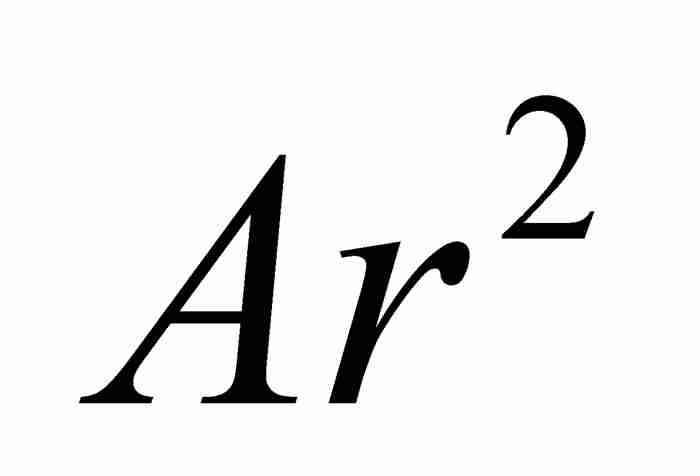 ,
, 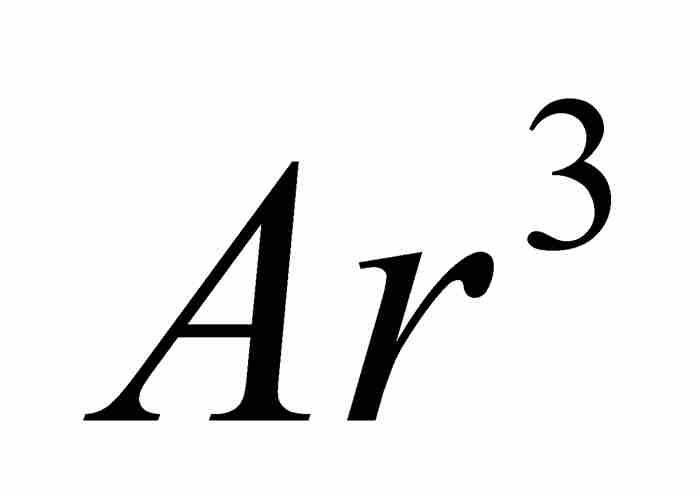 , …,而將等差數列寫成
, …,而將等差數列寫成 ,
, 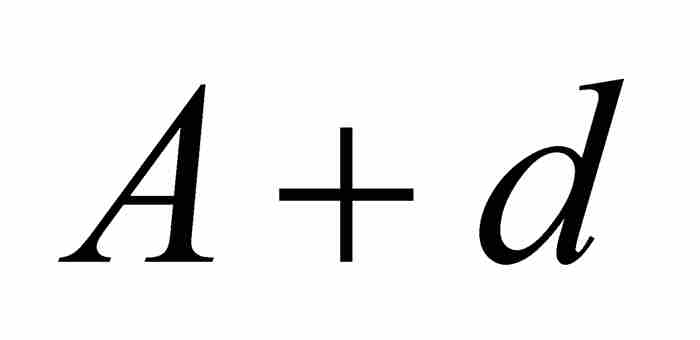 ,
, 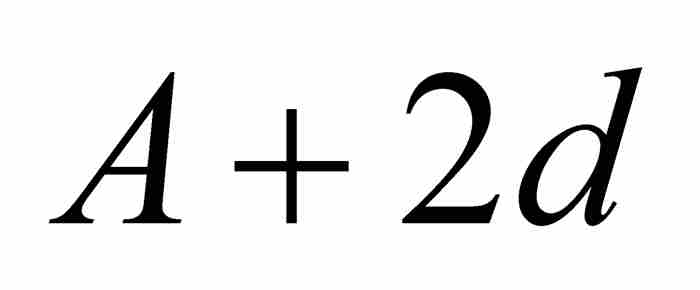 ,
, 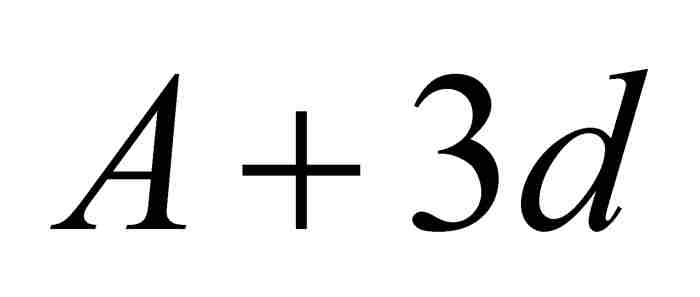 , …。
, …。
作為雅各布的《論無窮級數及其有限和》的第4個命題,他證明了關於前兩項相同的正數項等比數列和等差數列的一個引理。
定理 如果A, B, C,…, D, E是公比為r>1的正數項的等比數列,而A, B, F,…, G, H也是從A和B開始的正數項的等差數列,那麼,等比數列中其餘每一項都大於對應的等差數列中的相應項。
證明 使用現代的記號,我們將等比數列表示為 ,
,  ,
, 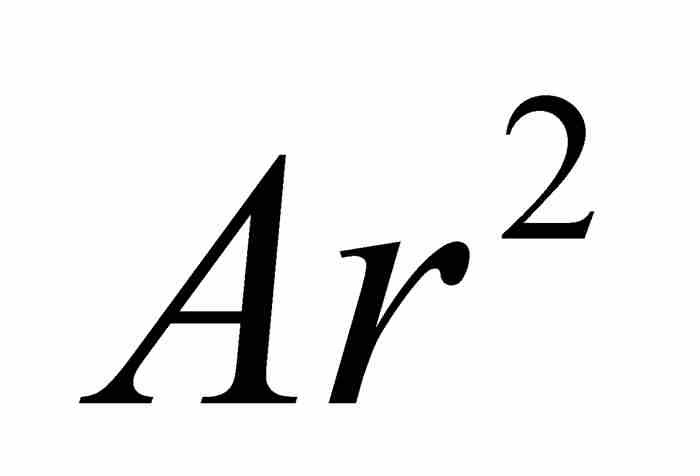 ,
, 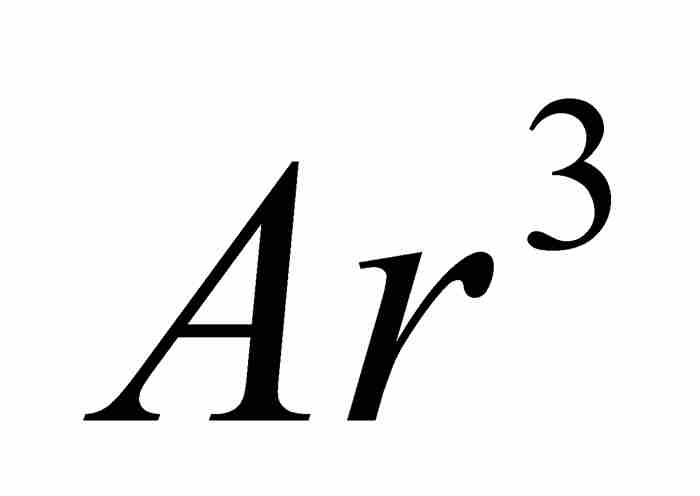 , … ,而將等差數列表示為
, … ,而將等差數列表示為 ,
, 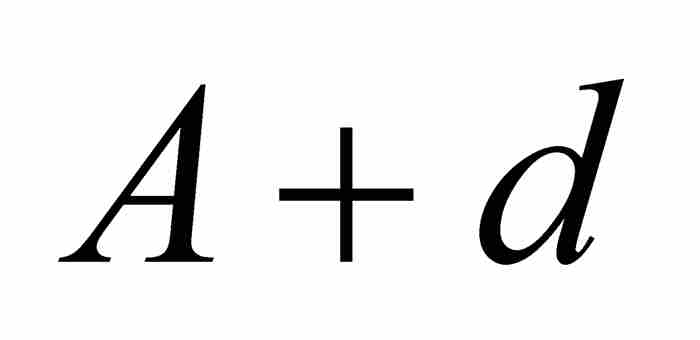 ,
, 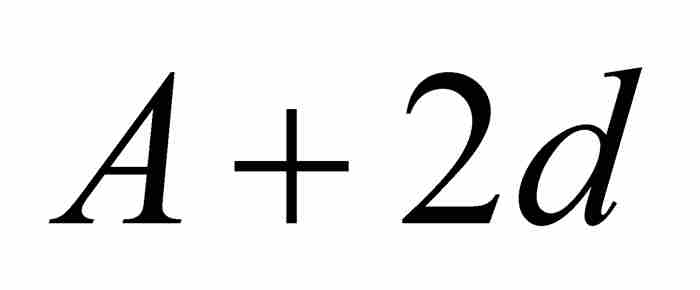 ,
, 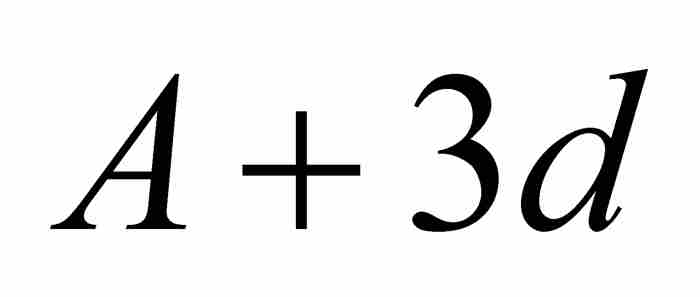 , …。根據假設,可知
, …。根據假設,可知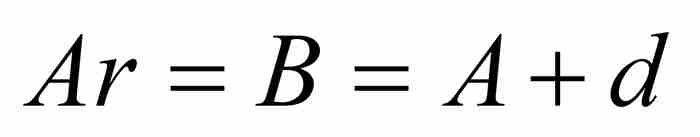 。由於
。由於 ,我們有
,我們有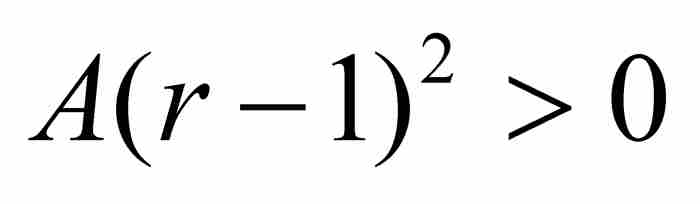 ,展開得到
,展開得到
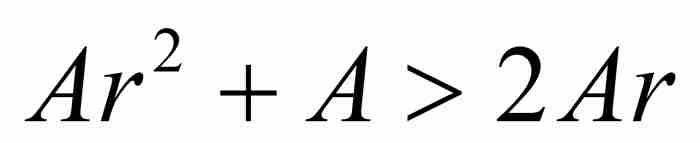
或者簡化成
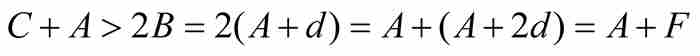
因此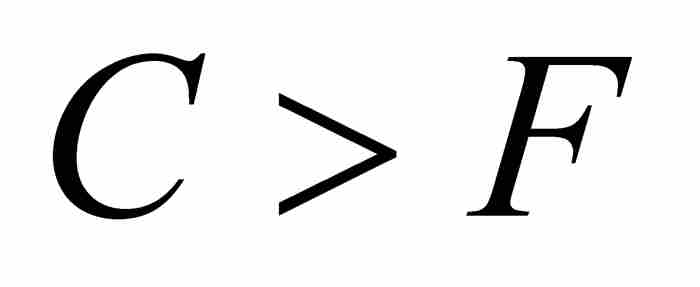 ,這就是說,如定理所述,等比數列的第3項大於等差數列的第3項。這個證明,可以重複到第4項、第5項以及此後的任何項。
,這就是說,如定理所述,等比數列的第3項大於等差數列的第3項。這個證明,可以重複到第4項、第5項以及此後的任何項。
在幾個命題之後,雅各布證明了在描述方式上帶有17世紀風格的下述結果。
定理 在任意有限項等比數列A, B, C, …, D, E中,第1項與第2項的比,等於除最後一項外所有項的和與除第1項外所有項的和的比。
證明 一旦我們掌握了不熟悉的數學語言,這是就很容易證明的,因為
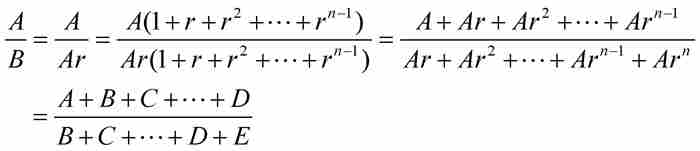
接下來雅各布求有限項等比數列的和。令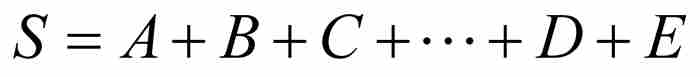 為待求的和,他應用上述結果得到
為待求的和,他應用上述結果得到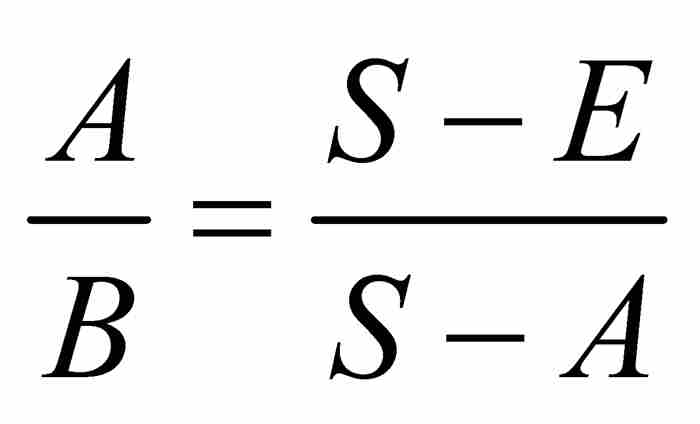 ,求解得
,求解得
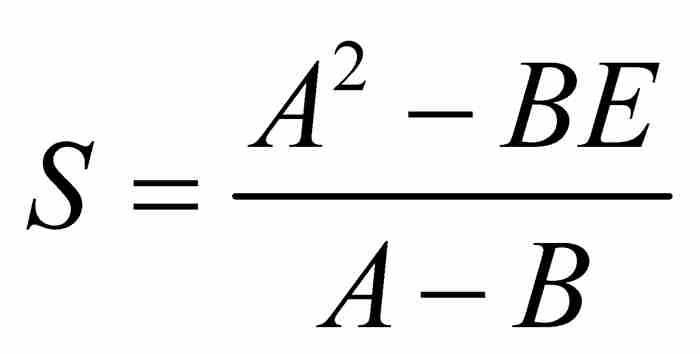 (1)
(1)
注意式(1)用到了有限等比數列的第1項(A)、第2項(B)和最後一項(E)。這與我們今天看到的標準求和公式
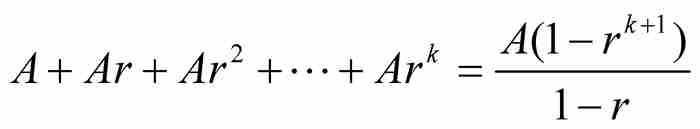
不同,這個公式利用的是第1項、項數和公比。
以這些預備知識做鋪墊,現在我們可以看看雅各布對調和級數進行的分析。此項分析在《論無窮級數及其有限和》一文中緊接在約翰的級數發散證明之後。4 將弟弟的成果包含在他的論文中也許顯得異乎尋常地慷慨,但是雅各布發起了挑戰,給出自己的另一個證明。用他的話說,目標是證明「無窮調和級數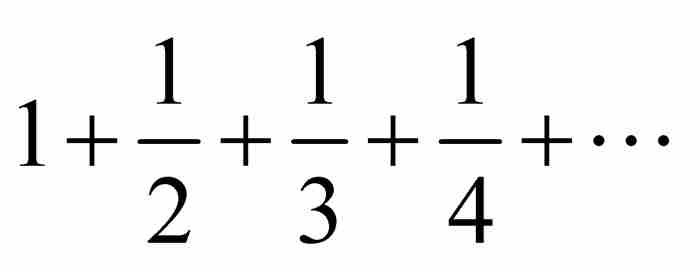 的和超過任意給定的數。因此,它的和為無窮大」。5
的和超過任意給定的數。因此,它的和為無窮大」。5
4 Jakob Bernoulli, Ars conjectandi, p. 250。
5 Jakob Bernoulli, Ars conjectandi, p. 251。
定理 調和級數發散。
證明 選擇任意自然數N,雅各布首先試圖從調和級數中去除從第1項開始的相繼若干項,這些項的和大於或等於1。他再從剩下的項中,去除和等於或大於1的相繼若干項。按這種方式進行下去,直到N次把這樣的有限項去除,使整個調和級數之和減少的值至少為N。由於N是任意的自然數,所以調和級數之和為無窮大。
倘若我們總是能去除和為1或更大的有限項,那麼從雅各布的文章中幾乎一字不差地抄錄下來的這個論證步驟就是正確的。為完成證明,伯努利必須證明這的確是事實。於是,他假定情況相反,就是說,「如果在去除一些項後,剩餘項之和不可能超過1,那麼,令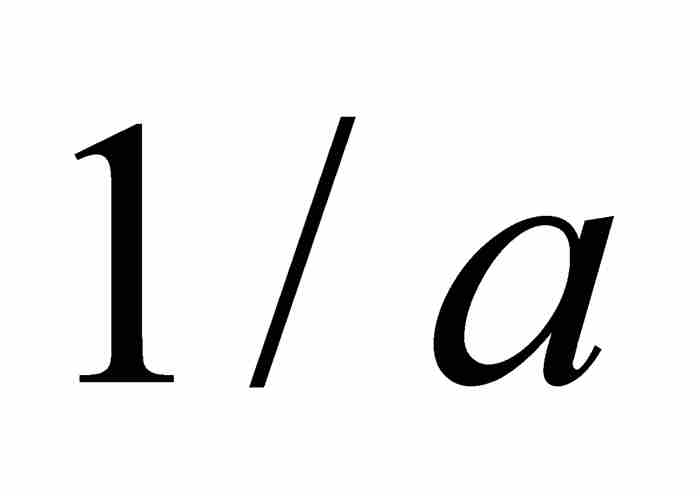 為最後一次去除有限項以後的第1項」。換句話說,為了引出矛盾,他假定不管達到多少項,
為最後一次去除有限項以後的第1項」。換句話說,為了引出矛盾,他假定不管達到多少項,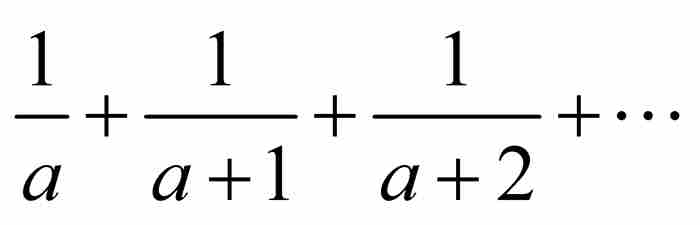 的和都小於1。但是這些分母
的和都小於1。但是這些分母 ,
, 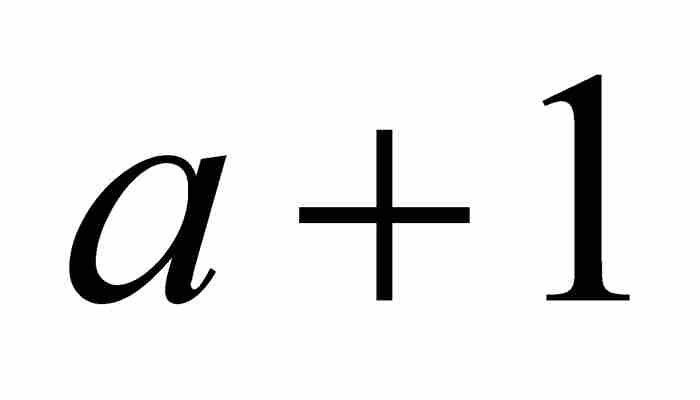 ,
, 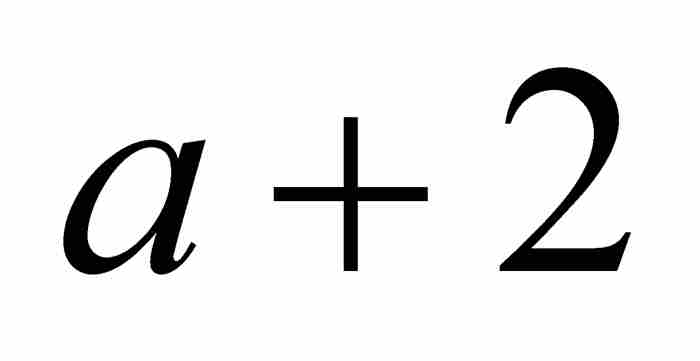 , …構成一個等差數列,因此雅各布引入與這個等差數列前兩項相同的等比數列。就是說,他考慮等比數列
, …構成一個等差數列,因此雅各布引入與這個等差數列前兩項相同的等比數列。就是說,他考慮等比數列 ,
, 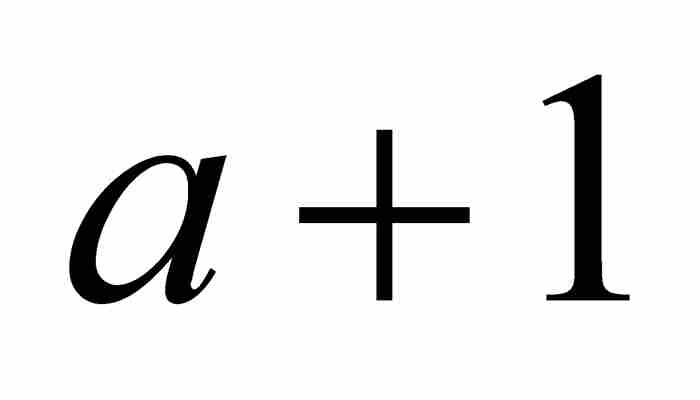 , C, D, …, K,其中他要求我們一直取到
, C, D, …, K,其中他要求我們一直取到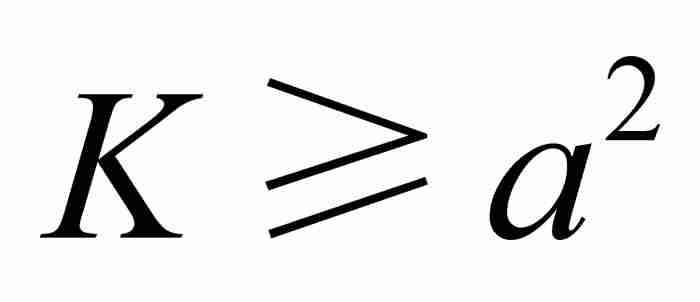 。這是可以做到的,因為數列的公比為
。這是可以做到的,因為數列的公比為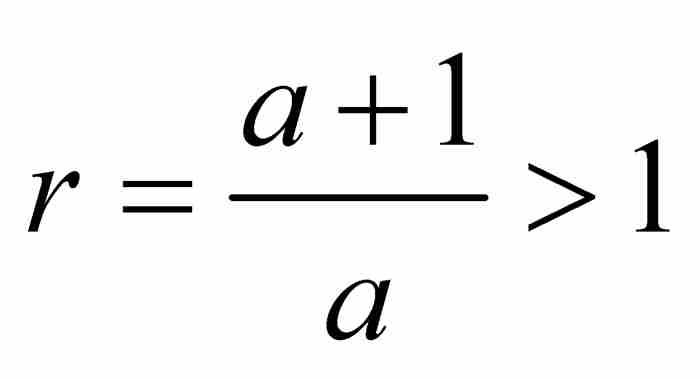 ,所以其項可以隨意地增大。
,所以其項可以隨意地增大。
如前所見,雅各布知道等比數列的每一項都大於對應的等差數列的相應項,因此,他取倒數,推出
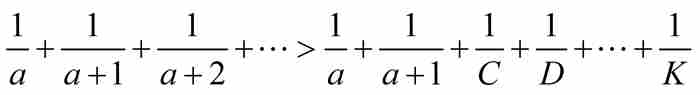
其中不等式左邊具有的(有限)項數同右邊的項數相等。雅各布使用式(1)計算這個等比數列的和,其中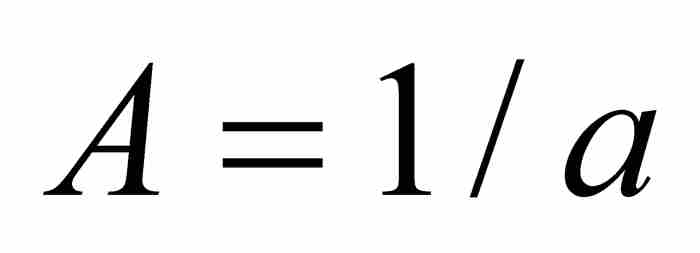 ,
,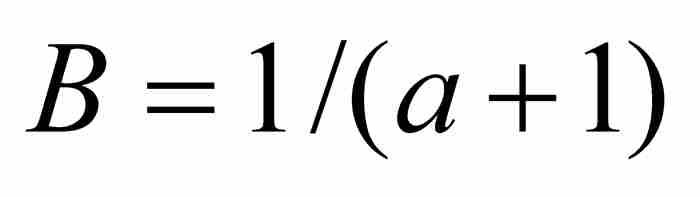 ,而
,而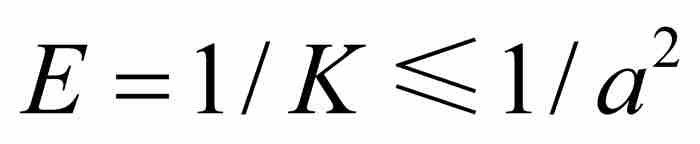 ,得到
,得到
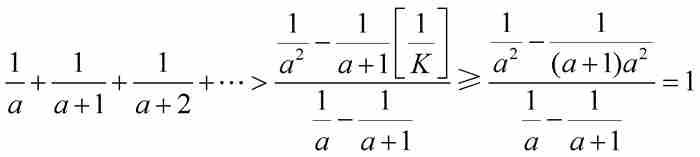
這與他最初的假設矛盾。通過這種方式,雅各布斷定,從調和級數的任何一項開始,其剩餘部分的某個有限項的和必然超過1或者更大。
為了完成證明,他使用下面的方式重新組合調和級數:
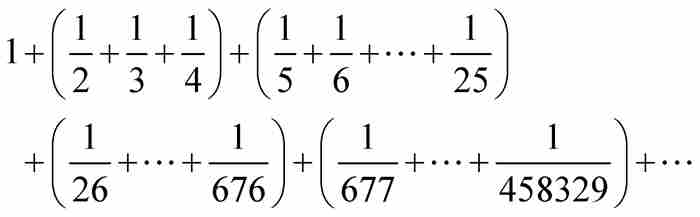
其中每個括號中的表達式都超過1。因此,所得的和可以比任何預先指定的數大,所以調和級數發散。
這是一個構思巧妙的證明。雅各布很清楚它的重要意義,他強調,「一個最後項趨近零的無窮級數的和也許是有限的,也許是無限的」。6自然,不會有現代數學家談論無窮級數的「最後項」,但是雅各布的意圖是清楚的:即使無窮級數的一般項縮小至零,也不足以保證級數收斂。調和級數就是一個極好的例子。雅各布·伯努利因此證明了這一點,今天大家依然採用這個證明。
6 Jakob Bernoulli, Ars conjectandi, p. 252。
雅各布和他的垛積級數
調和級數之所以被關注是因為它的不良特性,即發散性。受到同樣關注的是具有有限和這種良好特性的無窮級數。雅各布從等比級數開始並巧妙地對其進行改變,計算了一些非同一般的級數的精確值。下面我們考察其中幾個級數。
首先,他需要求無窮等比數列的和。如式(1)所示,伯努利使用公式
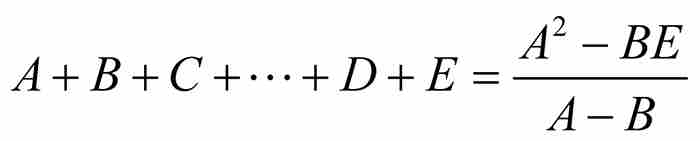
求出有限等比數列的和。他注意到一個必然結果,由正數構成的公比小於1的無窮等比數列的一般項必定趨近零。因此,他簡單地令他的「最後」項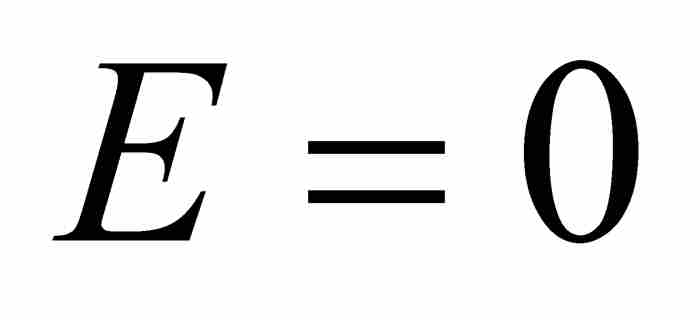 ,得到
,得到
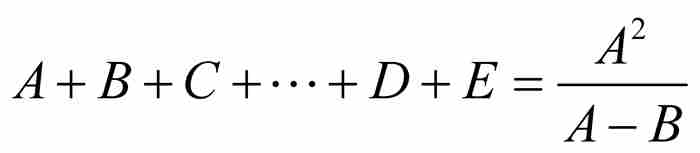 (2)
(2)
等差數列和等比數列並不是17世紀的數學家們唯一熟悉的數列形式。他們也熟悉「垛積數」,這是同某些幾何形體(如三角形、稜錐體和立方體)相關的整數的家族。例如我們有三角形數1, 3, 6, 10, 15, …,這樣命名是因為它們來源於圖3-1所示的不斷擴展的三角形中的點數。容易看出,第k個三角形數是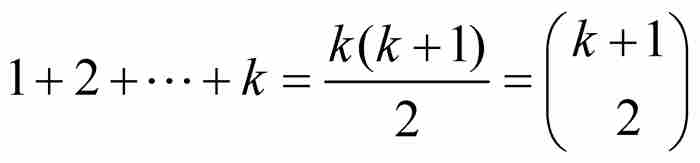 ,其中的二項式係數是在雅各布·伯努利之後才出現的記號。
,其中的二項式係數是在雅各布·伯努利之後才出現的記號。
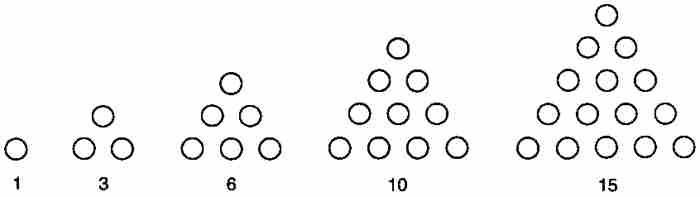
圖 3-1
同樣,稜錐體數是1, 4, 10, 20, 35, …,它們是以三角形為底的稜錐垛中彈丸的數目。可以證明,第k個稜錐體數是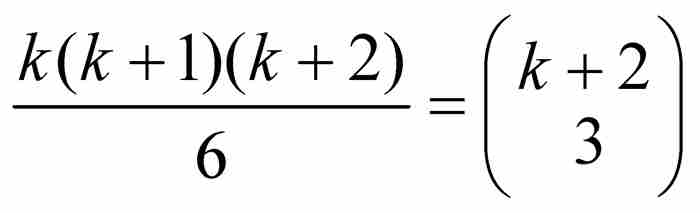 。自然,正方形數1, 4, 9, 16, 25, …和立方體數1, 8, 27, 64, 125, …同樣有其幾何意義。
。自然,正方形數1, 4, 9, 16, 25, …和立方體數1, 8, 27, 64, 125, …同樣有其幾何意義。
伯努利在這方面的研究興趣表現為如下形式:他想求出無窮級數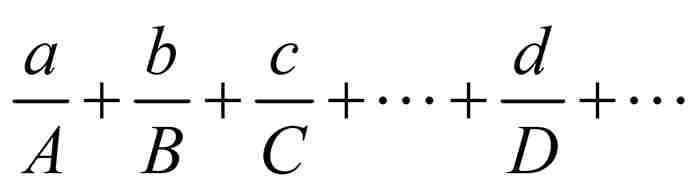 的精確和,其中,分子a, b, c, …, d, …是垛積數,而分母A, B, C, …, D, …構成等比數列。例如,他想要計算
的精確和,其中,分子a, b, c, …, d, …是垛積數,而分母A, B, C, …, D, …構成等比數列。例如,他想要計算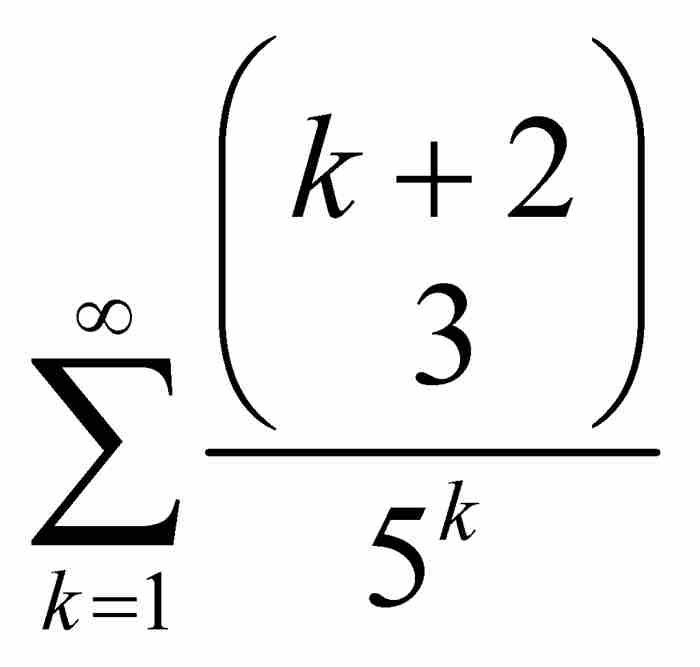 或者
或者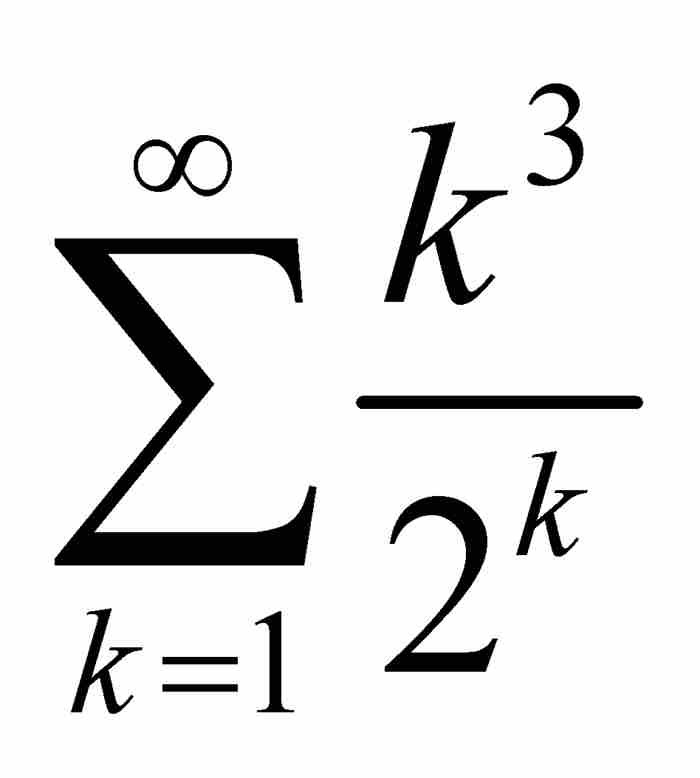 這樣一些級數的和。當時,這種求和是極具挑戰性的問題。
這樣一些級數的和。當時,這種求和是極具挑戰性的問題。
雅各布解決這類問題的辦法是先解決簡單問題,再解決複雜問題,在數學上,這始終是一種正確的策略。仿照他的論證過程,我們從以自然數為分子和等比數列為分母的無窮級數著手。1
1 Jakob Bernoulli, Ars conjectandi, pp. 246-249。
定理N 如果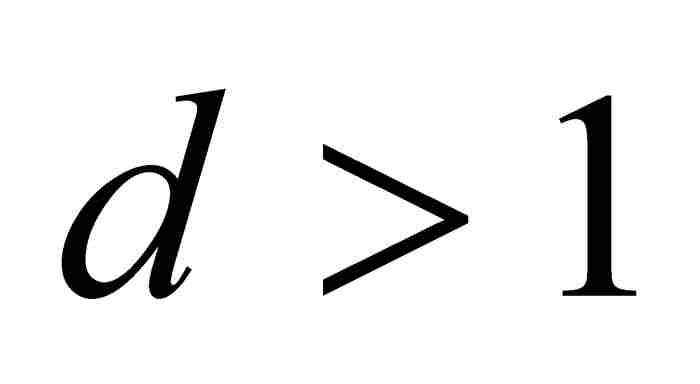 ,那麼
,那麼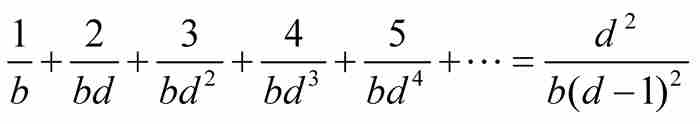 。
。
證明 雅各布令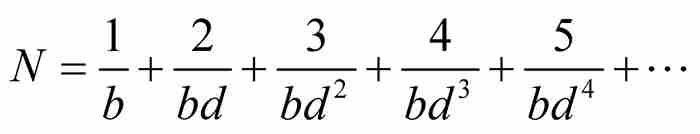 ,然後將其分解為一系列無窮等比數列,再利用式(2)對每個數列求和:
,然後將其分解為一系列無窮等比數列,再利用式(2)對每個數列求和:
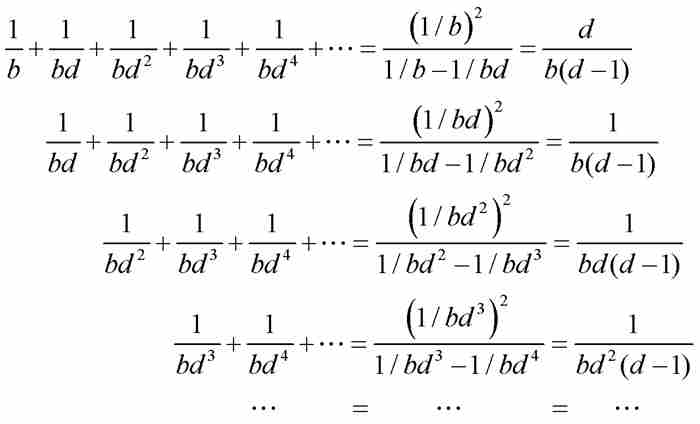
對上述等式按列相加,他求出
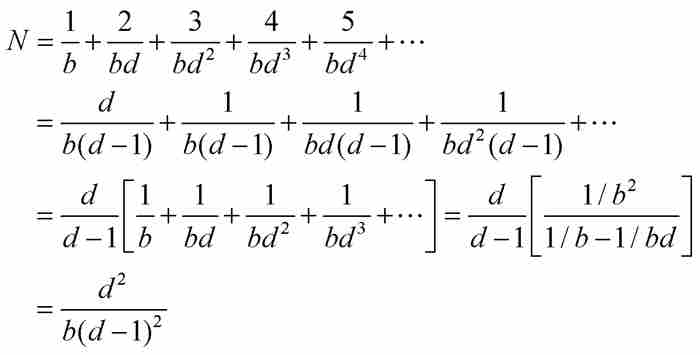
因為方括號中的無窮級數又是等比級數。
例如,當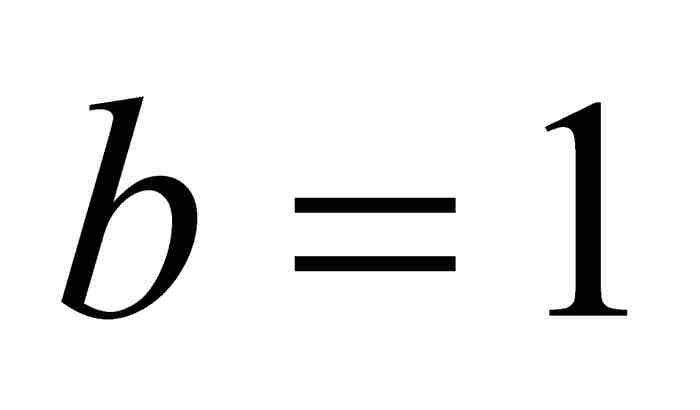 和
和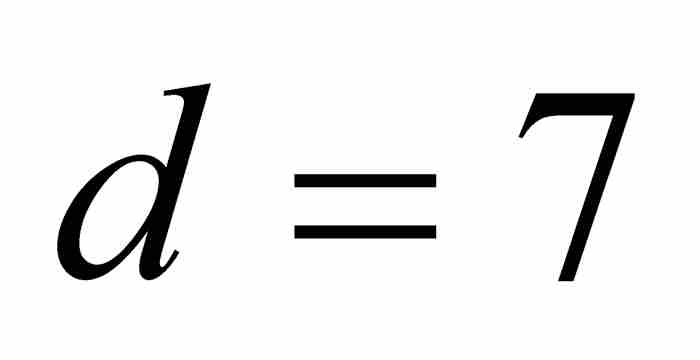 時,可得
時,可得 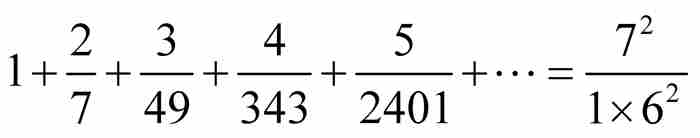
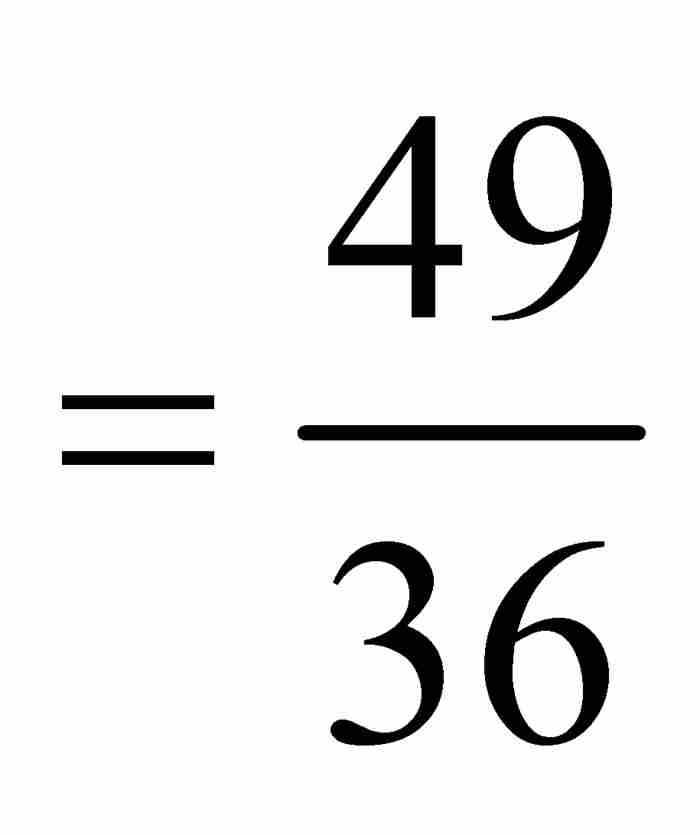 。
。
下一步,雅各布將分子換成三角形數。
定理T 如果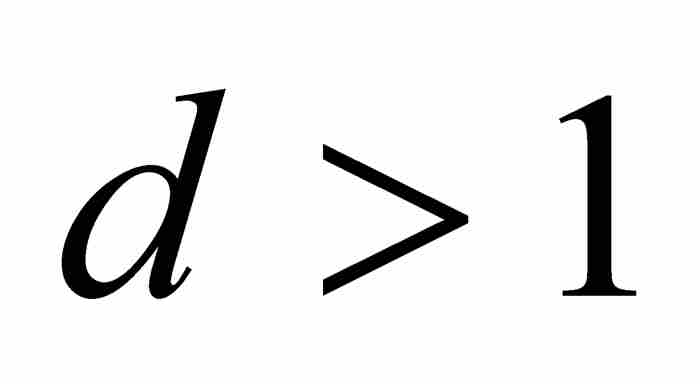 ,那麼
,那麼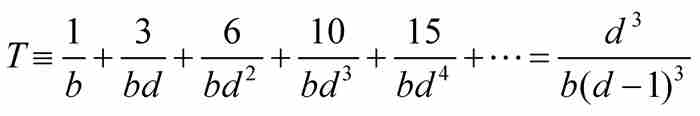 。
。
證明 竅門是將T分解成一系列等比級數,並且利用第k個三角形數為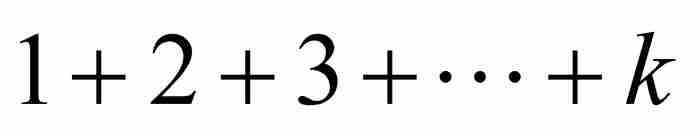 這個事實:
這個事實:
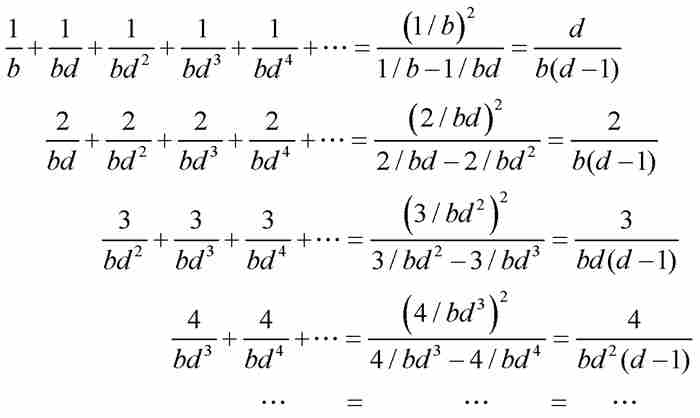
對上述等式按列相加,得到
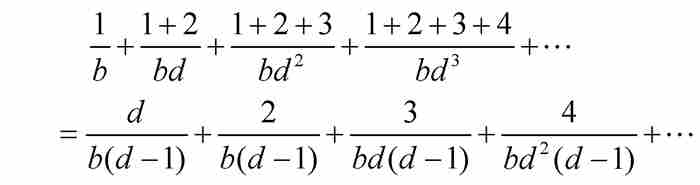
換句話說,由定理N可得
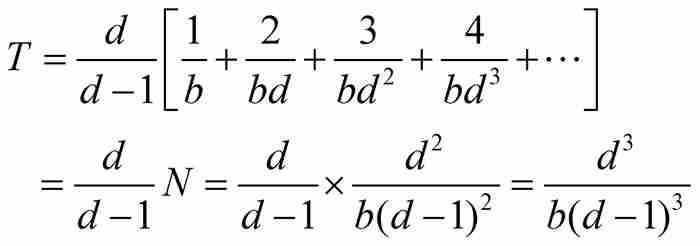
例如,當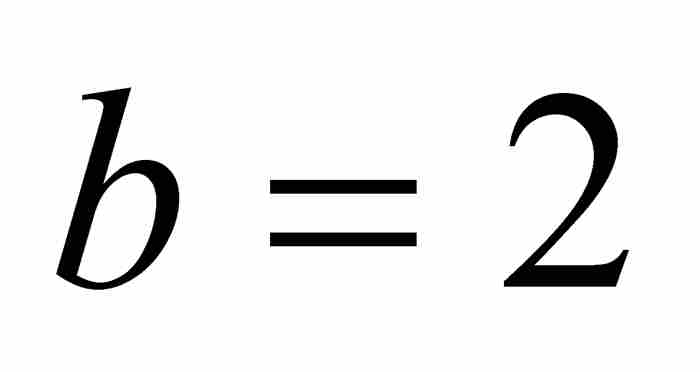 和
和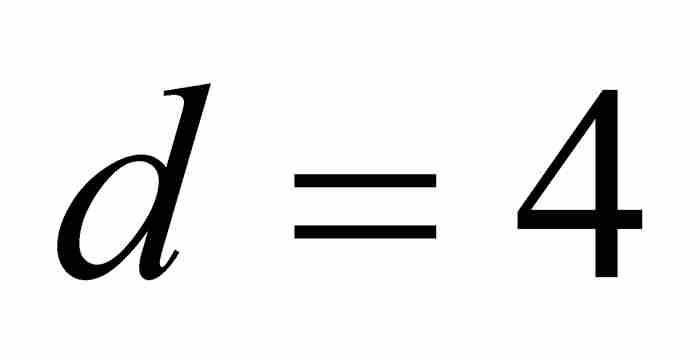 時,有
時,有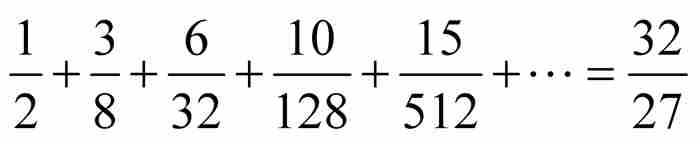 。
。
接下來雅各布考慮分子為稜錐體數的情況。
定理P 如果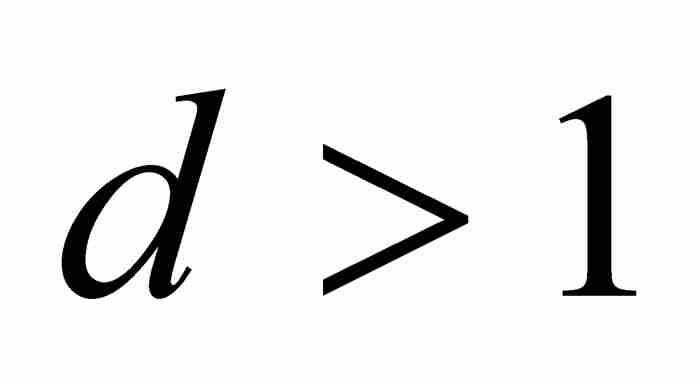 ,那麼
,那麼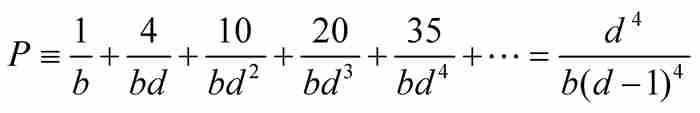 。
。
證明 這個證明很簡單,因為
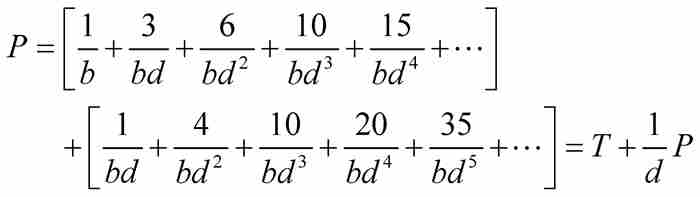
由於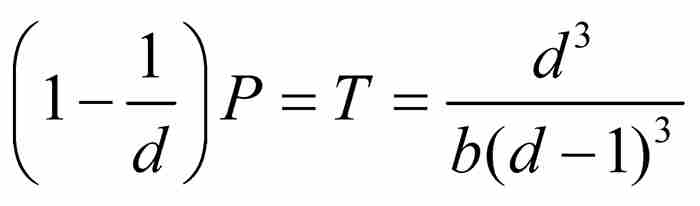 ,所以
,所以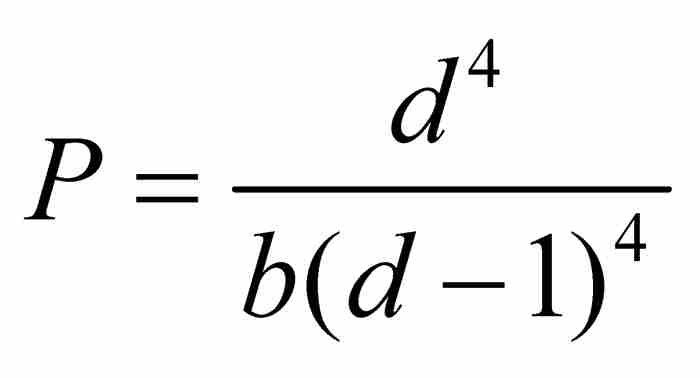 。
。
例如,當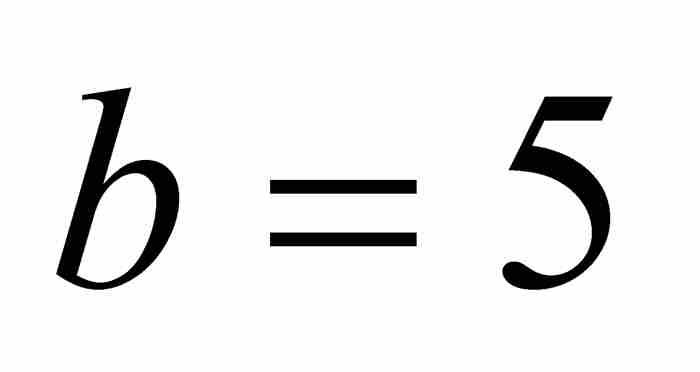 和
和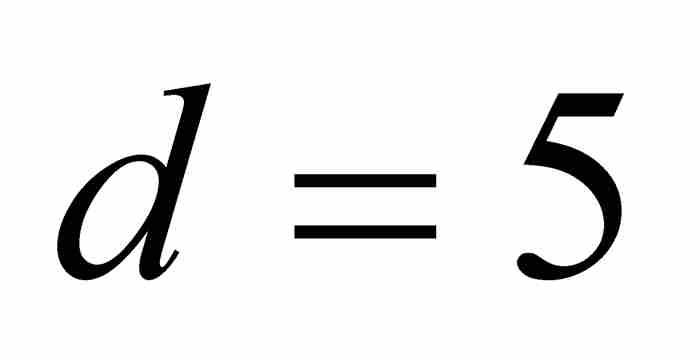 時,可得
時,可得
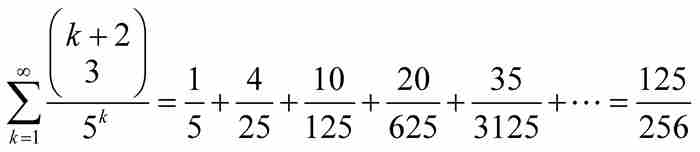
在《論無窮級數及其有限和》一文中這一部分的最後,雅各布討論了以立方體數為分子和等比數列為分母的無窮級數。
定理C 如果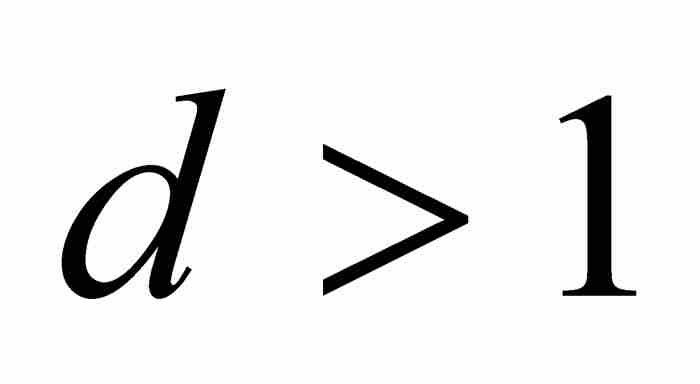 ,那麼
,那麼
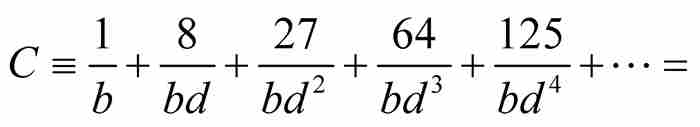
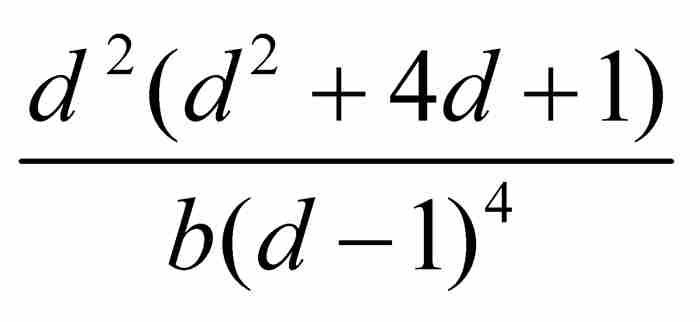
證明
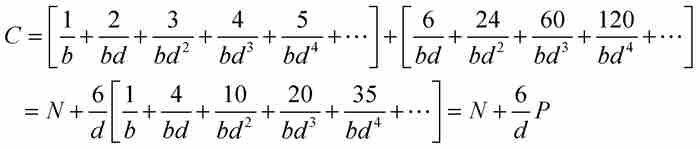
所以
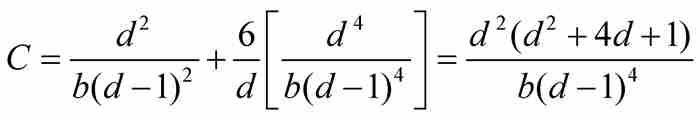
當雅各布令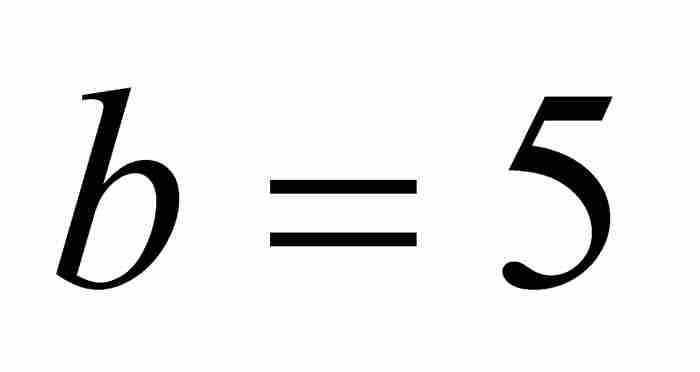 和
和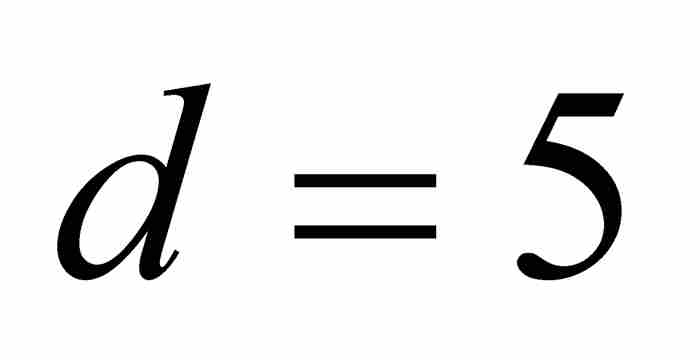 時,他得到精確的和:
時,他得到精確的和:
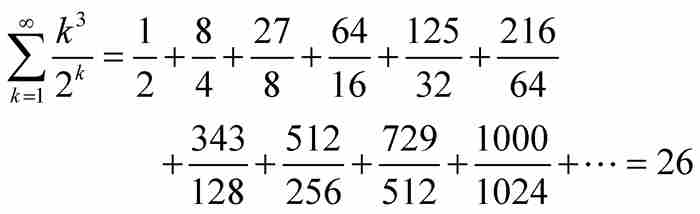
這是一個令人驚奇而又非直觀的結果。
在取得這些成果之後,雅各布·伯努利也許開始感到無往而不勝了。倘若他當時真地懷有這種想法,很快也會轉變態度的,因為由平方數的倒數構成的級數,即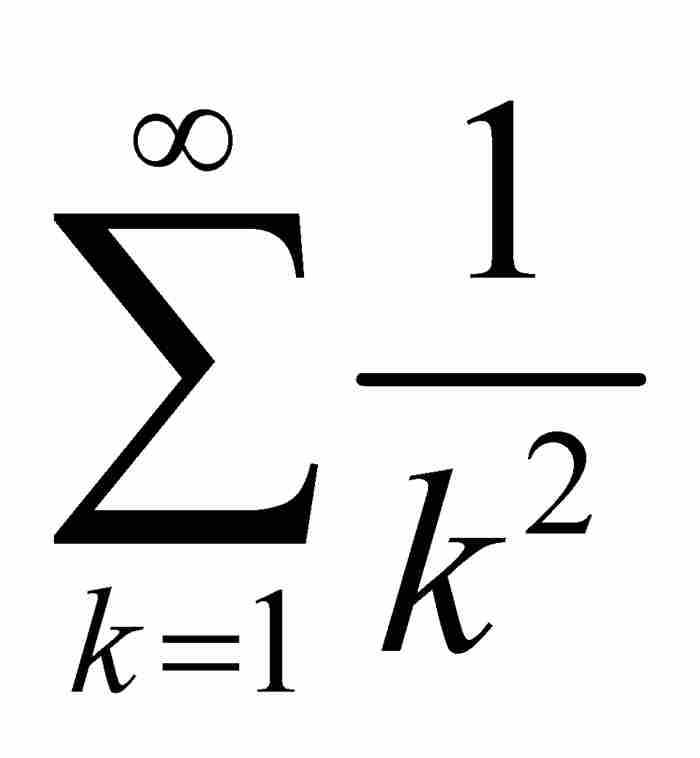 ,擋住了他的去路。他可以採用我們現在所知的比較檢驗法證明這個級數收斂於某個小於2的數,但是他未能求出這個數。雅各布收起了他的傲慢,在他的《論無窮級數及其有限和》中提出了這樣的懇求:「如果誰能解決並告知這個我們無能為力的問題,我們將不勝感謝。」2
,擋住了他的去路。他可以採用我們現在所知的比較檢驗法證明這個級數收斂於某個小於2的數,但是他未能求出這個數。雅各布收起了他的傲慢,在他的《論無窮級數及其有限和》中提出了這樣的懇求:「如果誰能解決並告知這個我們無能為力的問題,我們將不勝感謝。」2
2 Jakob Bernoulli, Ars conjectandi, p. 254。
正如我們在後面要看到的,對於伯努利提出的難題,整整一代人不得其解,直到最後由歷史上最卓越的分析學家之一的歐拉給出問題的答案。
雅各布·伯努利堪稱一位無窮級數的大師。他那位具有同樣天賦的弟弟約翰有著自己感興趣的研究領域。下面我們來討論其中約翰稱為「指數微積分」的問題。
約翰和x^x
在1697年的一篇論文中,約翰·伯努利從下述一般法則開始他的討論:「一個對數函數無論多麼複雜,它的微分等於函數表達式的微分除以表達式。」 1 例如,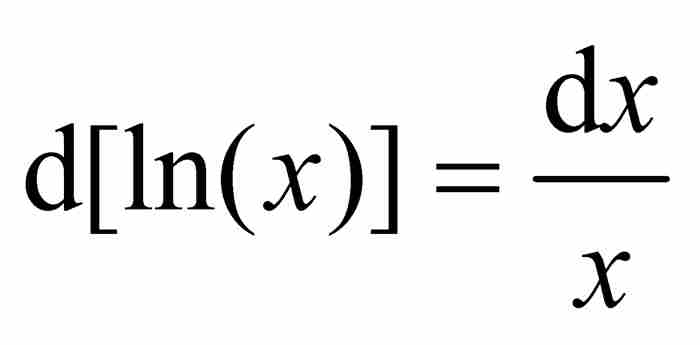 ,或者
,或者
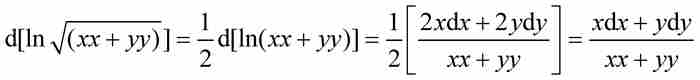
1 Johannis Bernoulli, Opera omnia, vol.1, Georg Olms, Hildesheim, 1968, p. 183。
在最後的這個表達式中,我們保留了伯努利的原有記號。在當時的數學出版物中,高次冪的寫法與現在相同,但是通常把平方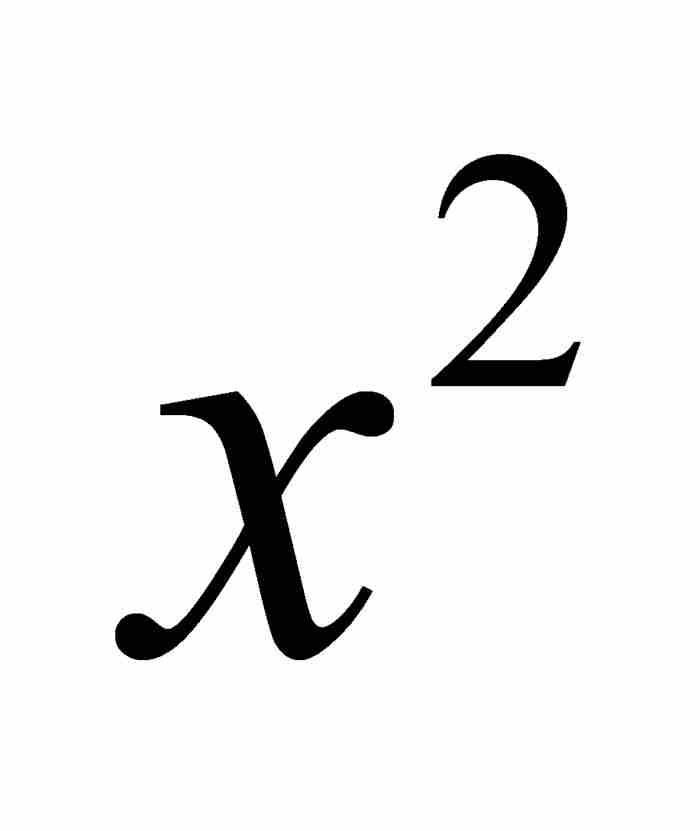 寫成
寫成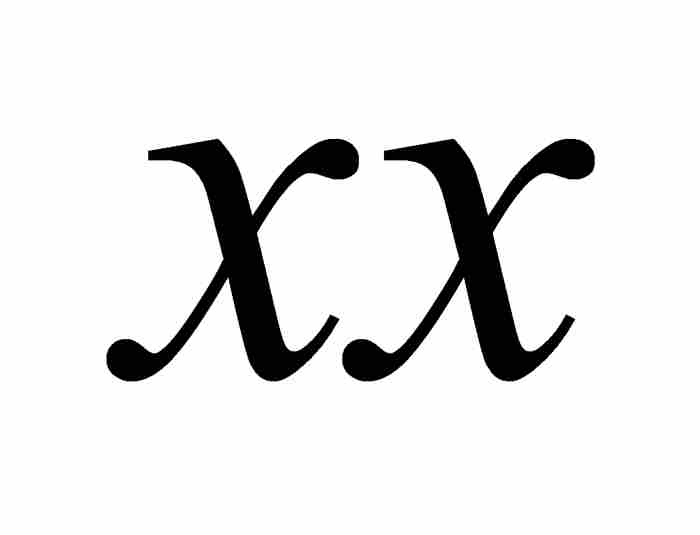 。此外,順便說一下,伯努利還用lx表示
。此外,順便說一下,伯努利還用lx表示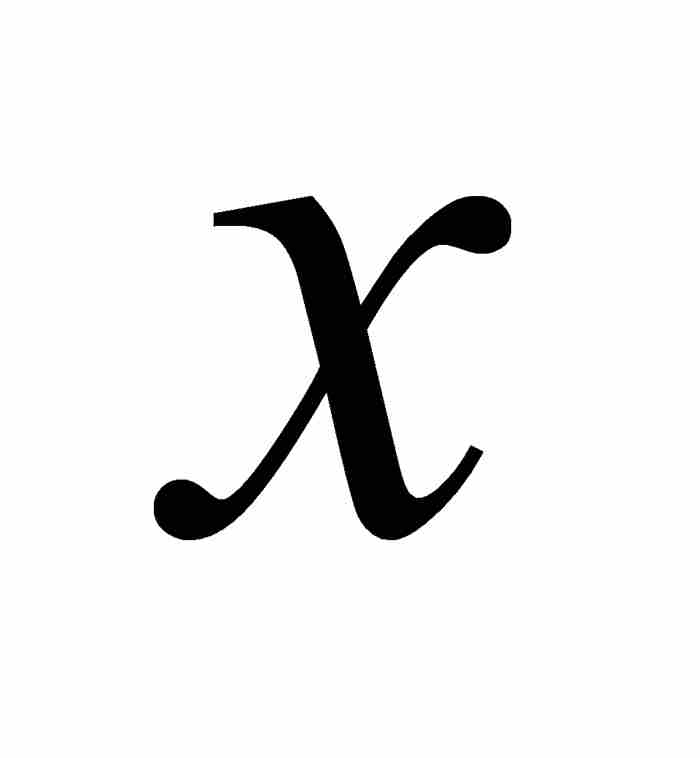 的自然對數。
的自然對數。
約翰給出了對應的積分公式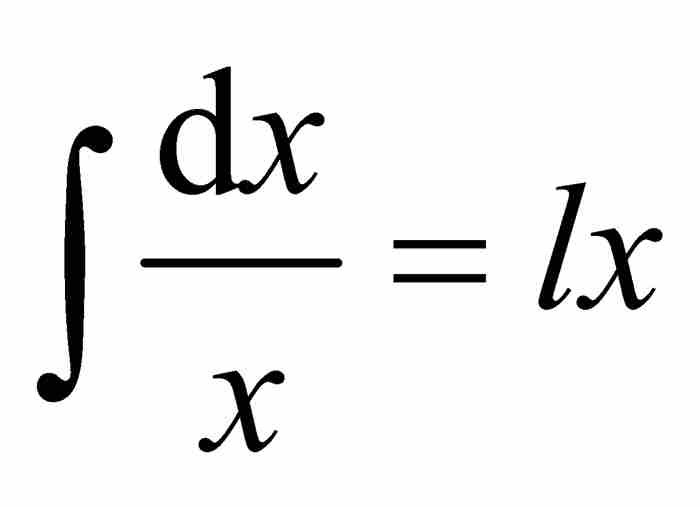 。在他學術生涯的早期,對於這一點的理解極為混亂,他相信
。在他學術生涯的早期,對於這一點的理解極為混亂,他相信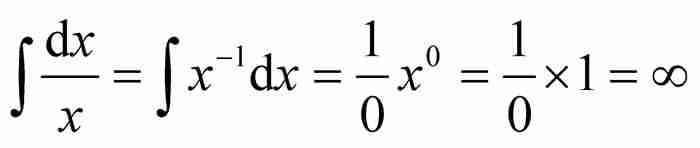 ,這是一種對指數法則的濫用,今天許多初學微積分的學生也有這樣的錯誤理解。2 幸好約翰改正了他的錯誤。
,這是一種對指數法則的濫用,今天許多初學微積分的學生也有這樣的錯誤理解。2 幸好約翰改正了他的錯誤。
2 Johannis Bernoulli, Opera omnia, vol.3, p. 388。
憑借這些預備知識,約翰作出承諾,他要用「由我首先創立的」法則去獲取豐碩的知識成果,「用以前沒有被發現的或者不是廣為人知的知識去充實這座新的微積分的寶庫」。3 也許他最感興趣的例子莫過於圖3-2所示的曲線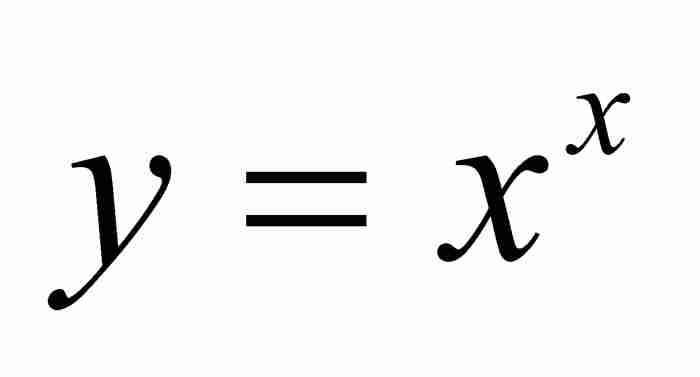 。
。
3 Johannis Bernoulli, Opera omnia, vol.3, p. 376。
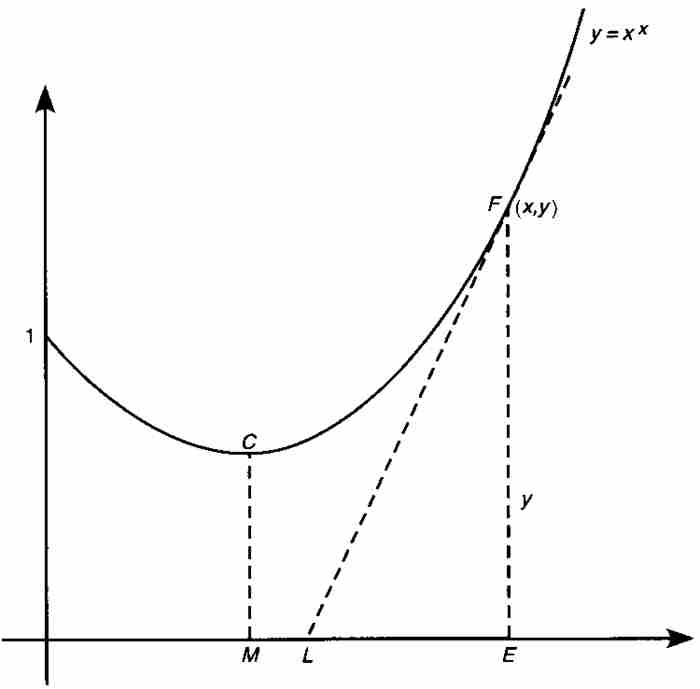
圖 3-2
約翰從曲線上任意一點F求出次切距,即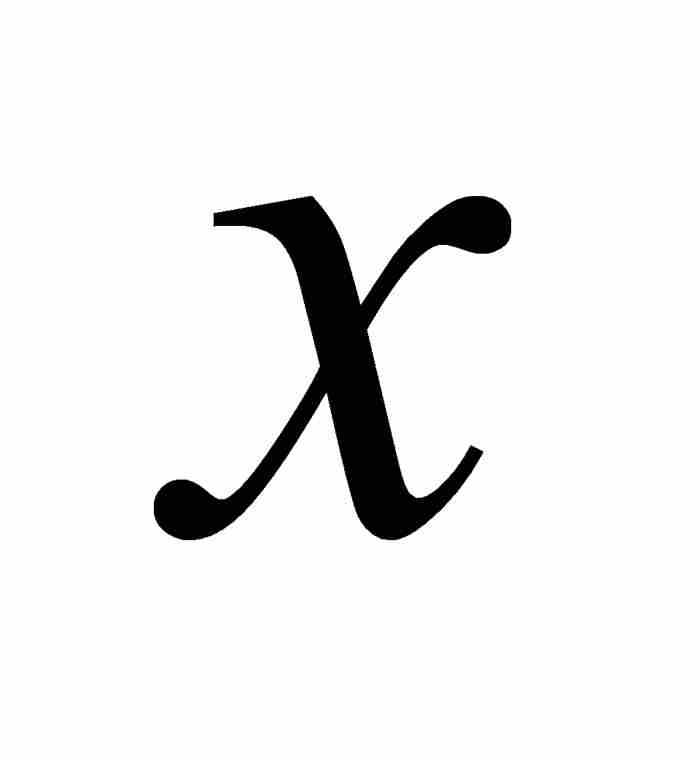 軸上切線下方的線段LE。為做到這一點,他首先對曲線方程兩端取對數:
軸上切線下方的線段LE。為做到這一點,他首先對曲線方程兩端取對數: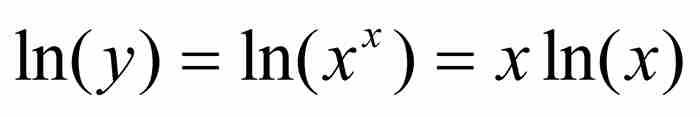 。然後他利用自己的法則求微分:
。然後他利用自己的法則求微分:
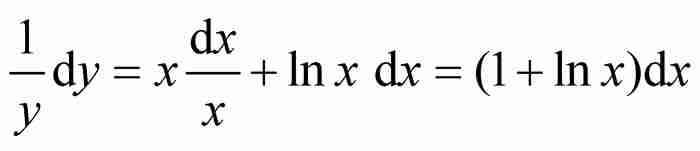
但是,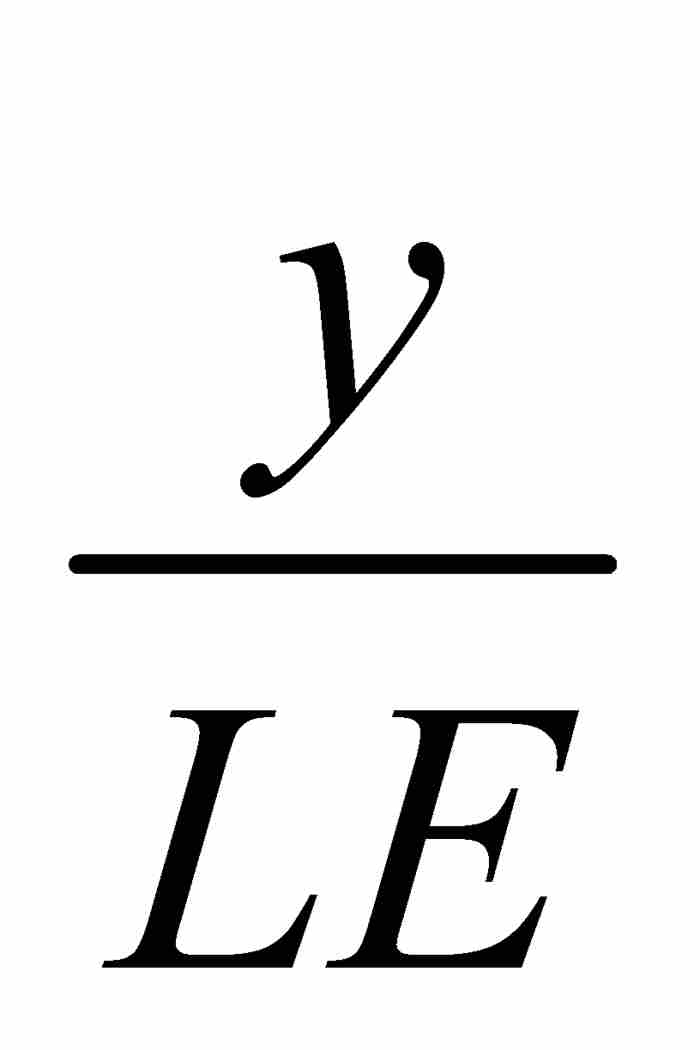 =切線的斜率=
=切線的斜率=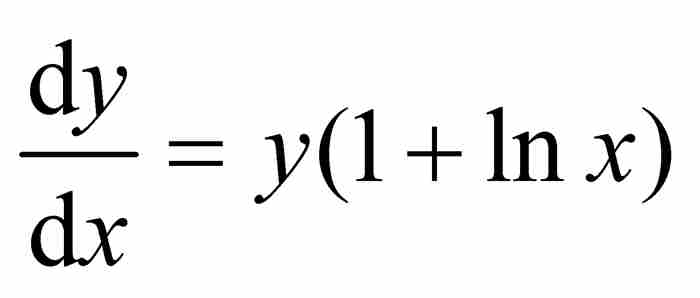 ,他由此求出次切距的長度
,他由此求出次切距的長度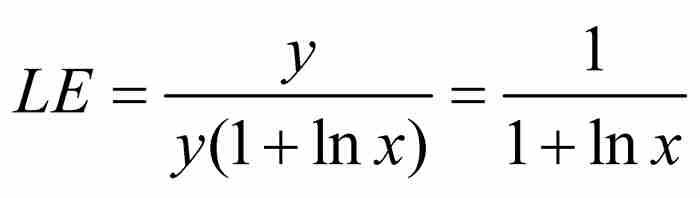 。
。
伯努利下一步就是尋找曲線的極小值,他將其稱為「所有縱坐標的最小值」。當切線處於水平方向或者等價於次切距為無窮大時,得到曲線的極小值。為了確定當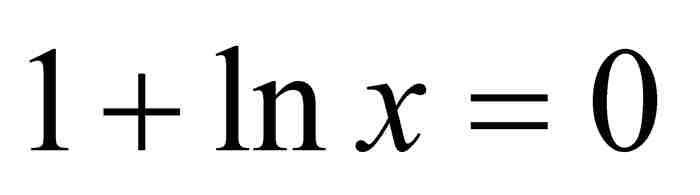 時x的值,約翰描述了一個頗為複雜的幾何步驟。4
時x的值,約翰描述了一個頗為複雜的幾何步驟。4
4 Johannis Bernoulli, Opera omnia, vol.1, pp. 184-185。
他的推理無懈可擊,但是他的答案的形式按照當今的判別標準,看起來不是最佳的。由於指數函數的引進是幾十年之後的事情,所以,約翰受到制約,他缺乏一種用於簡單表達結果的記號。現在我們可以求出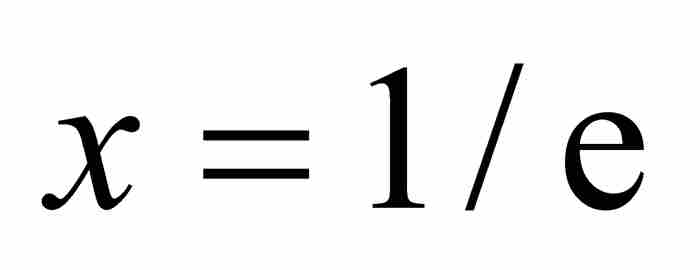 ,再確定xx的最小值,也就是圖3-2中線段CM的長度,等於
,再確定xx的最小值,也就是圖3-2中線段CM的長度,等於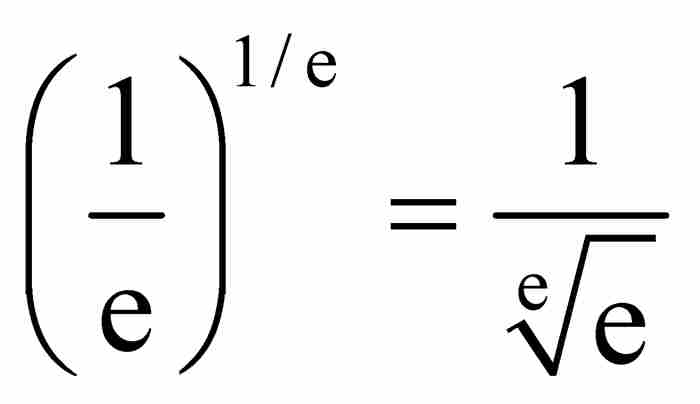 ,這個值近似為0.6922。不言而喻,這個答案決不是顯而易見的。
,這個值近似為0.6922。不言而喻,這個答案決不是顯而易見的。
至此,約翰只不過作好了繼續前進的準備。他在1697年的另一篇論文中,解決了一個更為棘手的問題:求他的曲線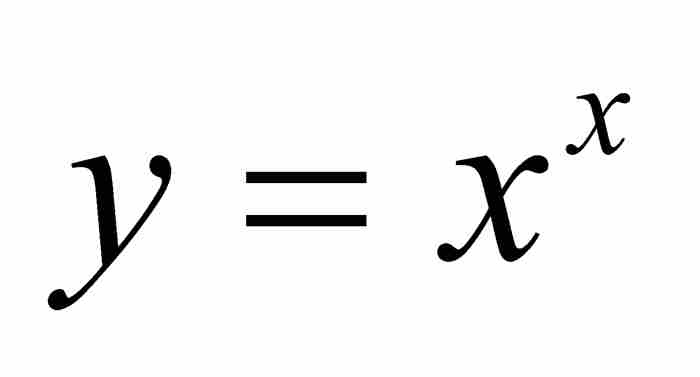 之下從
之下從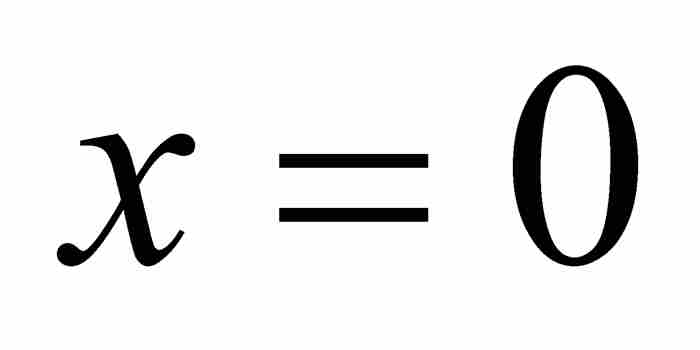 到
到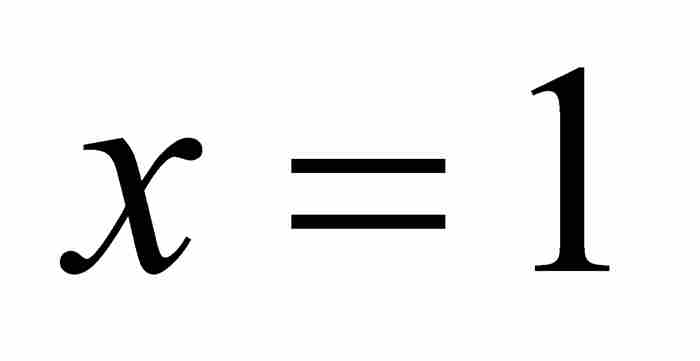 的區域的面積。就是說,他想求
的區域的面積。就是說,他想求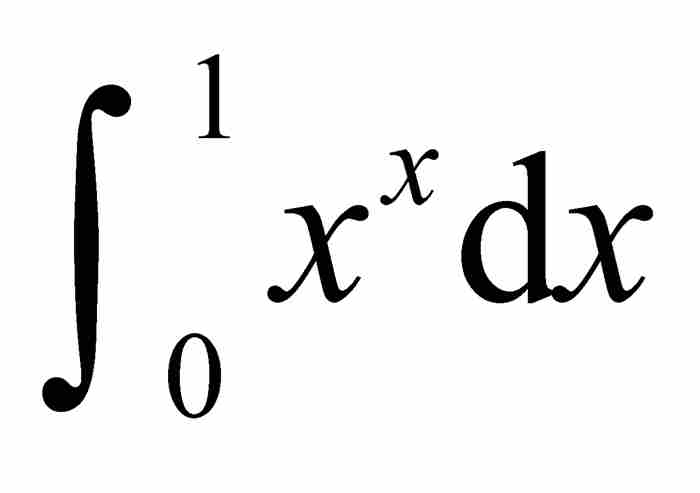 的值。相當令人吃驚,他求出了他一直試圖尋找的答案。5
的值。相當令人吃驚,他求出了他一直試圖尋找的答案。5
5 Johanis Bernoulli, Opera omnia, vol.3, pp. 376-381。
這個論證需要兩個前提條件。他將第一個條件表述如下:
如果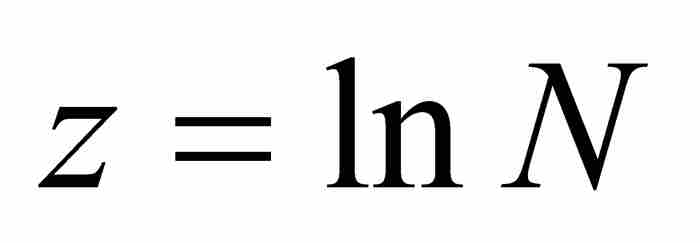 ,那麼
,那麼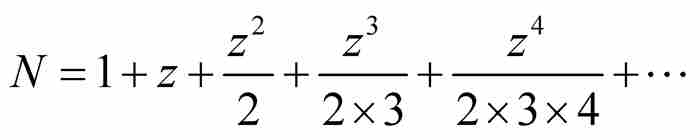
從這裡,我們看出N的表達式是指數級數。如果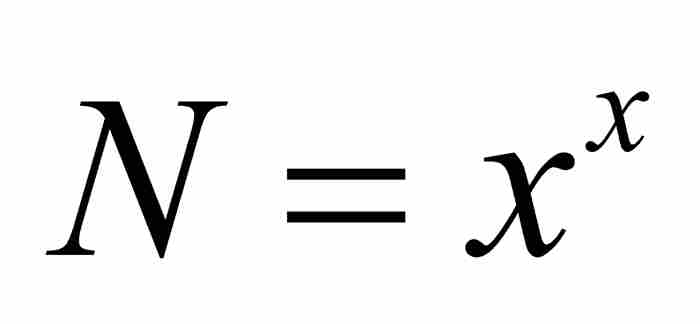 ,那麼
,那麼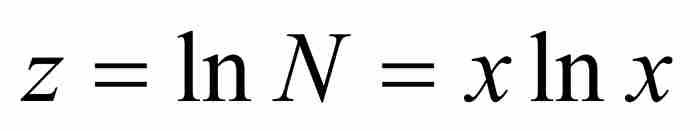 ,而約翰推導出
,而約翰推導出
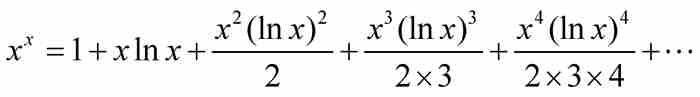 (3)
(3)
約翰的目標是通過對每一項積分求和來求這個和的積分。為此,他需要求積分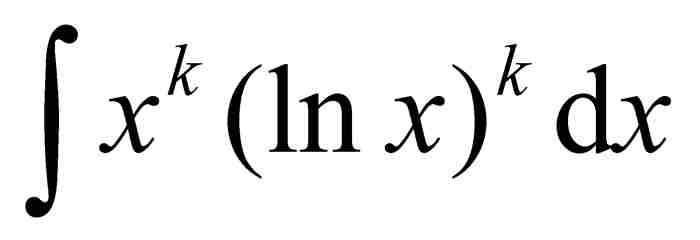 的公式。他採用遞歸的方法產生如下所示的積分表。
的公式。他採用遞歸的方法產生如下所示的積分表。
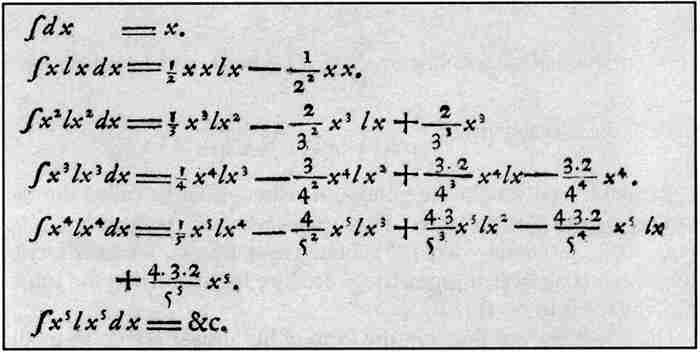
約翰·伯努利的積分表(1697)
一種現代的方法則是利用分部積分證明約化公式
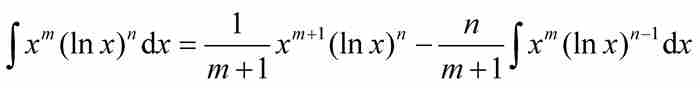 (4)
(4)
對於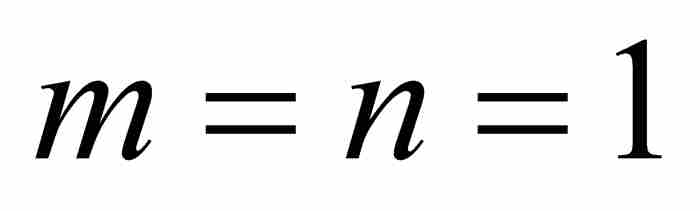 ,式(4)中的遞歸公式給出
,式(4)中的遞歸公式給出
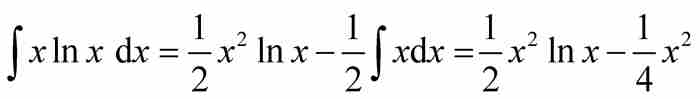
(像伯努利和他同時代的數學家一樣,我們忽略了積分公式後面的任意常數項「+C」。)對於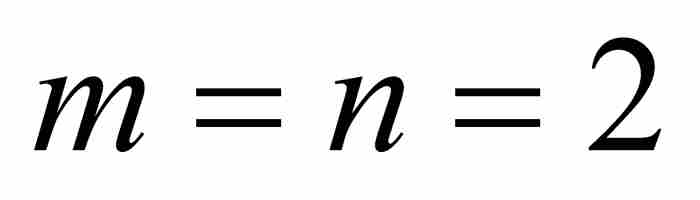 ,得到
,得到
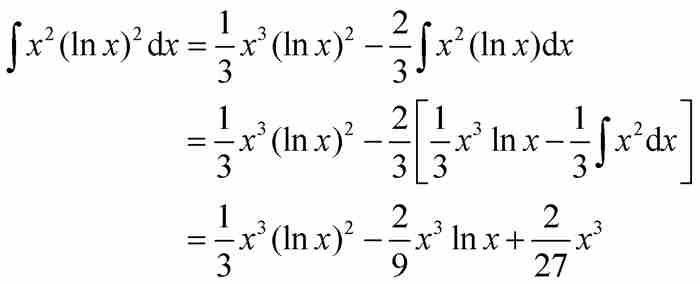
其中我們已經應用了取m=2和n=1時的公式(4)。
通過這種方式,我們重新得到了伯努利的積分表。同式(3)的指數級數一樣,這也是求解他的奇特問題的關鍵。
定理 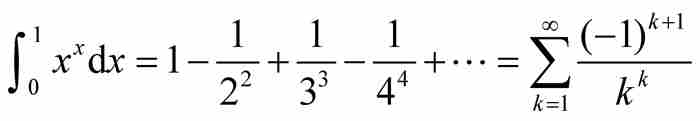 。
。
證明 由式(3),
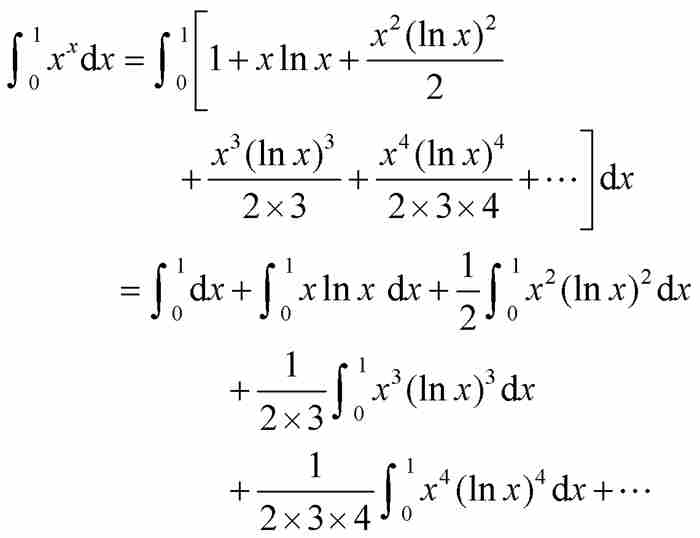
其中伯努利毫不猶豫地用積分的級數替換了級數的積分。他利用他的積分表中的公式繼續推導:
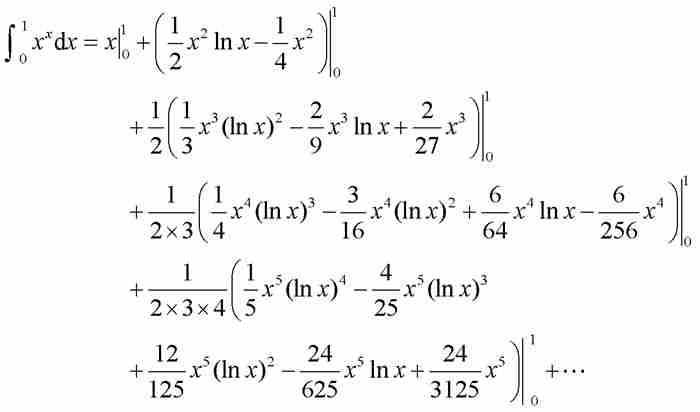
在這裡,他注意到代入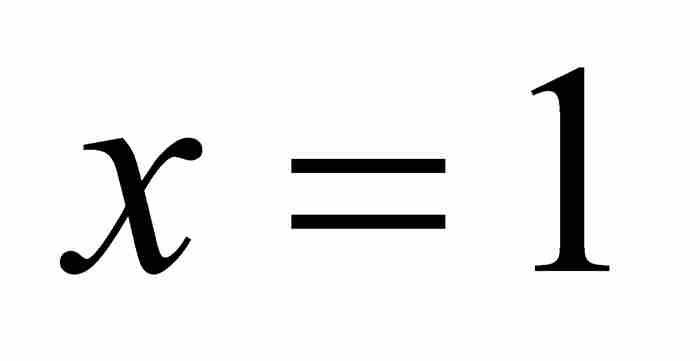 ,「所有含自然對數lx或lx任意乘方的項都化為零,因為1的對數等於零」。6 這是很精彩的,但是現代讀者可能感到困惑,因為他沒有提及代入x = 0會產生像
,「所有含自然對數lx或lx任意乘方的項都化為零,因為1的對數等於零」。6 這是很精彩的,但是現代讀者可能感到困惑,因為他沒有提及代入x = 0會產生像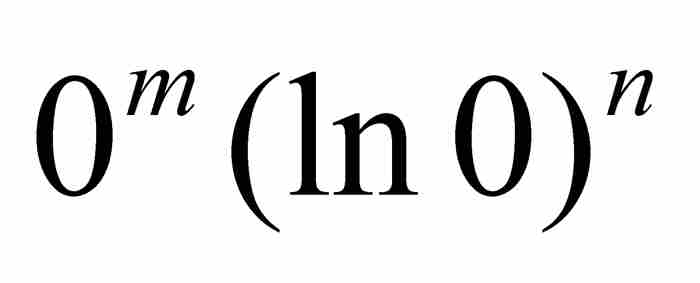 這樣的不定式。今天,我們可以應用洛必達法則(最恰當的選擇!)證明
這樣的不定式。今天,我們可以應用洛必達法則(最恰當的選擇!)證明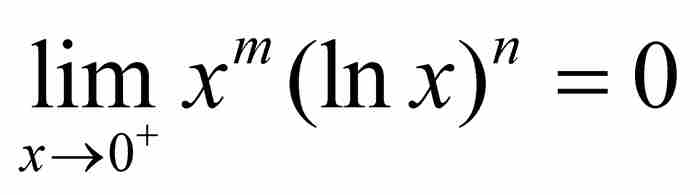 。
。
6 Johanis Bernoulli, Opera omnia, vol.3, p. 381。
在任何情況下,在如此多的項消失以後,伯努利保留下
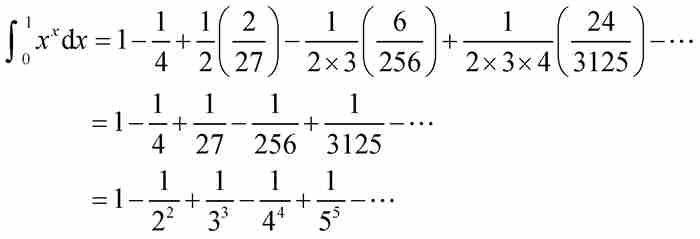
這個級數給出曲線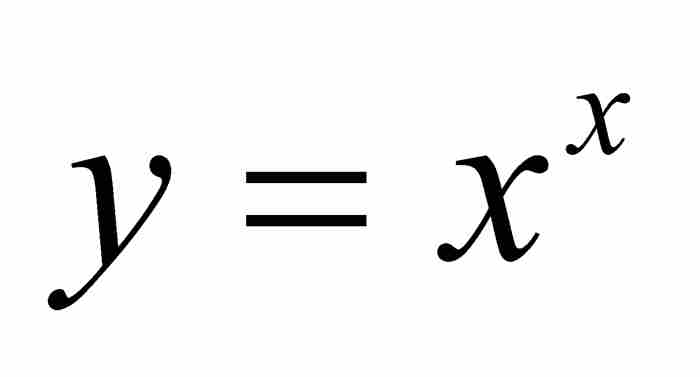 下單位間隔內的面積,這是十分引人注目的。除了級數極好的對稱性和直觀性以外,約翰還發現了它具備另外一種特性。他寫道:「這個奇妙的級數收斂得非常快,第10項的值只佔總和的10億分之一。」 7 無疑,僅需要計算很少的幾項就得到
下單位間隔內的面積,這是十分引人注目的。除了級數極好的對稱性和直觀性以外,約翰還發現了它具備另外一種特性。他寫道:「這個奇妙的級數收斂得非常快,第10項的值只佔總和的10億分之一。」 7 無疑,僅需要計算很少的幾項就得到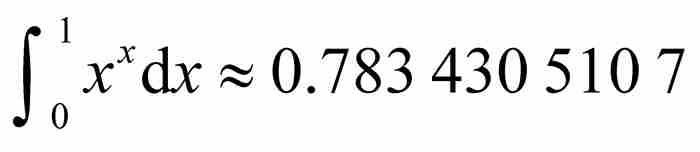 ,這是精確到第10位小數的數值。
,這是精確到第10位小數的數值。
7 Johanis Bernoulli, Opera omnia, vol.3, p. 377。
從本章的例子明顯看出,雅各布·伯努利和約翰·伯努利確實是戈特弗裡德·威廉·萊布尼茨的得意門生。用現在的話來說,萊布尼茨的微積分在他們的手中變成「用戶友好的」。這兄弟二人使在他們之前原本很深奧的微積分成為非常容易理解的學科。
此外,約翰還留下了另外一份「遺產」。在18世紀20年代,他培養了一名前途無量的年輕的瑞士學生。這位學生的名字是萊昂哈德·歐拉,我們將在下一章介紹他的成就。
