12堂魔力數學課：第9章用途多多的三角學_阿瑟·本傑明

如何測量一座山的高度

三角學可以幫助我們解決經典幾何學無法搞定的幾何問題。例如，請大家考慮下面這個問題。

問題：利用量角器和袖珍計算器測量附近山峰的高度。

我會給出5種解題方法，其中前3種方法幾乎不需要使用任何數學知識！

方法1（暴力測量法）：爬到山頂，將計算器扔到山腳下（需要力氣足夠大），測量計算器落到地面所需的時間（也許你會聽到山下傳來爬山者的尖叫聲）。如果測量結果為t秒，同時我們不考慮空氣阻力和終端速度等因素，那麼根據標準物理學方程式，我們可以計算出山的高度大約是16t2英尺。但是，由於空氣阻力和終端速度等因素的影響力非常顯著，因此你的計算結果準確度不高。此外，你的計算器也可能找不回來了。而且，如果應用這個方法，你還需要計時設備，這個計時設備可能正好安裝在你的計算器上。這個方法的好處是無須使用量角器。

方法2（戶外運動愛好者問詢法）：[1]找到一名態度友好的護林員，把那個漂亮的量角器送給她，請她告訴你這座山的高度。如果找不到護林員，就在附近找一名皮膚黝黑的男士，這樣的人長期在戶外活動，或許知道這個問題的答案。這個方法的好處是可以讓你交到一名新朋友，而且不需要犧牲你的計算器。此外，如果你對這位皮膚黝黑的戶外運動愛好者的答案有所懷疑，你還可以爬到山頂，用第一種方法測量山峰的高度。這個方法的缺點是你將失去量角器，還有可能受到行賄指控。

方法3（指示牌法）：在使用第一種和第二種方法之前，看看附近是否有說明山峰高度的指示牌。這個方法的好處是無須犧牲任何物品。

當然，如果你對這些方法都不感興趣，那麼你只能借助數學方法了。本章將告訴大家如何利用數學方法解決此類問題。

三角學、三角形和三角函數

「trigonometry」（三角學）的希臘字根是「trigon」和「metria」，意思是三角形測量。我們先來分析一些經典的三角形。

等腰直角三角形。等腰直角三角形包含一個90°的角，且另外兩個角必須相等。也就是說，除直角以外的兩個角都是45°（因為三角形的內角和為180°）。因此，我們把等腰直角三角形稱為45–45–90三角形。如果兩個直角邊長為1，根據勾股定理，斜邊的長度必然是。注意，如下圖所示，所有等腰直角三角形的邊長比都是1︰1︰。

45 – 45 – 90三角形的邊長比是1︰1︰

30 – 60 – 90三角形。等邊三角形的所有邊長都相等，所有角都是60°。如下圖所示，如果將等邊三角形分成兩個完全相等的部分，所得到的兩個直角三角形的三個內角分別是30°、60°和90°。如果等邊三角形的邊長為2，直角三角形的斜邊長就是2，短直角邊的邊長是1。根據勾股定理，長直角邊的邊長為。因此，所有30 – 60 – 90三角形的邊長比都是1︰︰2（我把它記作1︰2︰）。具體地說，如果斜邊長度為1，那麼另外兩邊的長度分別為1/2和 / 2。

30–60–90三角形的邊長比是1︰︰2

延伸閱讀

如果正整數a、b和c滿足a2 + b2 = c2，那麼我們把 (a, b, c) 稱為「勾股數」（Pythagorean triple）[2]。勾股數有無窮多個，其中最小、最簡單的勾股數是 (3, 4, 5)。當然，我們可以把這個勾股數擴大正整數倍，從而得到 (6, 8, 10)或(9, 12, 15) 或(300, 400, 500) 等勾股數。但是，我們關注的是更有價值的例子。下面介紹一種得到勾股數的方法。取任意正整數m、n，使m＞n。接下來，令

a = m2 – n2 b = 2mn c = m2 + n2

注意，a2 + b2 = (m2 – n2)2 + (2mn)2 = m4 + 2m2n2 + n4= (m2 + n2)2 = c2，也就是說，(a, b, c)是勾股數。例如，如果 m = 2，n = 1，就會得到 (3, 4, 5)。如果(m, n) = (3, 2)，就有勾股數 (5, 12, 13)；如果(m, n) = (4, 1)，就有 (15, 8, 17)；如果 (m, n) = (10, 7)，就有 (51, 140, 149)。令人吃驚的是，所有的勾股數都可以通過這個方法得到（所有數論課程都會證明這個結論）。

三角學建立在兩個重要函數的基礎之上，即正弦（sine）函數和餘弦（cosine）函數。如圖所示，已知直角三角形ABC，c表示斜邊長度，a、b分別表示∠A、∠B對應直角邊的長度。

對於角A（由於ABC是直角三角形，該角必然是銳角），我們把∠A的正弦函數（記作sinA）定義為：

sinA = = =

同理，我們把∠A的餘弦函數定義為：

cosA = = =

（注意，含有角A的所有直角三角形都與原三角形ABC相似，邊長的比例關係都相同，因此角A的正弦函數和餘弦函數與三角形的大小沒有關係。）

除正弦函數和餘弦函數之外，三角學中使用最多的函數就是正切（tangent）函數。我們把∠A的正切函數定義為:

tan A =

對於直角三角形，有：

tan A = ====

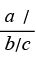關於正弦、餘弦和正切函數，有非常多種記憶方法，最常見的是「SOH CAH TOA」，其中SOH表示正弦為對邊（O）/斜邊（H），CAH、TOA與之類似。我的中學老師教給我的口訣是「Oscar Has A Heap of Apples」（奧斯卡有一堆蘋果），表示正弦、餘弦和正切函數分別對應OH、AH和OA。我的朋友對這個口訣進行了修改，把它變成：「Olivia Has A Hairy Old Aunt！（奧莉維亞的姑姑是一個粗魯的老婦人！）

例如，在下面這個3 – 4 – 5三角形中，有：

sinA = cosA = tan A =

對於3 – 4 – 5三角形而言，sinA = 3 / 5，cosA = 4 / 5，tan A = 3 / 4

那麼，這個三角形的∠B呢？計算角B的正弦與餘弦，就會發現：

sinB = = cosA cosB = = sinA

從計算結果可以看出，sinB = cosA，cosB = sinA。這並不是巧合，因為對於∠A而言，另一個銳角的對邊和鄰邊正好與之相反，但是斜邊保持不變。由於∠A + ∠B = 90°，對於任意銳角，我們都可以得到：

sin (90°– A ) = cosA cos (90°– A ) = sinA

例如，如果三角形ABC的∠A = 40°，那麼它的余角∠B = 50°且sin 50°= cos 40°，cos 50°= sin 40°。換句話說，角B的正弦等於角A的餘弦。

除此以外，你們可能還需要記住另外三個函數，不過它們的使用頻率低於前三個函數。這三個函數[分別是正割（secant）、余割（cosecant）和余切（cotangent）],它們的定義為：

sec A = csc A = cot A =

我們可以輕鬆證明正割與余割、正切與余切之間的關係和正弦與餘弦之間的關係相似，也就是說，對於直角三角形中的所有銳角，都有sec (90°– A ) = cscA，tan (90°– A ) = cot A。

學會計算正弦之後，就可以通過余角計算所有角的餘弦，進而求出正切和其他三角函數。但是，如何計算正弦呢？比如，40°的正弦是多少？最簡單的方法是利用計算器。我的計算器告訴我sin 40°= 0.642…，這個數值是如何計算出來的呢？在本章結尾，我將解釋其中的奧秘。

有些三角函數的值需要我們記住，而不需使用計算器。前面已經證明，30–60–90三角形的邊長比為1︰︰2，因此：

sin 30°= 1/2 sin 60°= / 2

還有：

cos 30°= / 2 cos 60°= 1 / 2

由於45 – 45 – 90三角形的邊長比1︰1︰，因此：

sin 45°= cos 45°= 1/ = /2

由於tan A =，因此我們只需記住tan 45°= 1和tan 90°不存在（因為cos 90°= 0），而無須記住其他正切函數的值。

在利用三角學計算山的高度之前，我們先解決一個簡單的問題：計算樹的高度。

如下圖所示，假設你與樹的距離是10英尺，樹的頂部與地面形成的仰角為50°。（順便告訴大家，大多數智能手機都有可以測量角度的應用程序。利用量角器、吸管和回形針等簡單工具，也可以製成一個有效的角度測量儀器——測角器。）

樹有多高？

如果樹的高度為h，就有：

tan 50°=

因此，h = 10 tan 50°。利用計算器可以算出它的值為10 ×1.19…≒ 11.9，也就是說樹的高度約為11.9英尺。

現在，我們準備利用第四種數學方法，解決前面提出的山高問題。我們面臨的難題是，我們不知道自己與大山中心點之間的距離。從本質上看，我們有兩個未知因素（大山的高度、大山與我們之間的距離），因此我們需要收集兩個信息。如下圖所示，假設從我們所在的位置看山頂的仰角是40°，然後背向大山走1 000英尺，這時的仰角變成32 °。接下來，我們利用這些信息來計算山的近似高度。

方法4（正切法）：如果山的高度為h，我們最初與大山之間的距離為x（x是的長度）。觀察直角三角形BCD，我們知道tan 40°≒ 0.839，因此：

tan 40°≒ 0.839 =

也就是說，h = 0.839x。根據三角形ABC，有：

tan 32°≒ 0.625 =

因此，h = 0.625 (x + 1 000) = 0.625x + 625。

從兩個等式中消去h，就可以得到：

0.839x = 0.625x + 625

該方程式的解為 x = 625 / (0.214) ≒ 2 920。也就是說，h的近似值為0.839 ×2 920 = 2 450。因此，山的高度約為2 450英尺。

單位圓、正弦定理與餘弦定理

到目前為止，我們都是利用直角三角形來定義各個三角函數的，而且我強烈建議大家無須思考，因為你們只要記住這些定義即可。但是，這些定義有一個缺點：只在角的度數為0°~90°時（直角三角形一定有一個90°角和兩個銳角），我們才能求出它的正弦、餘弦和正切。本節將討論如何利用單位圓來定義三角函數，這種定義法可以幫助我們求出任意角的正弦、餘弦和正切。

請大家回顧一下單位圓的定義：以圓點 ( 0, 0 ) 為圓心，以1為半徑的圓。在上一章，我們利用勾股定理推導出單位圓的方程式為 x2 + y2 = 1。如下圖所示，假設從點 (1, 0) 開始沿圓周逆時針方向運動構成的銳角A在單位圓上所對應的點為 (x, y) ，請大家確定該點的坐標。

單位圓上與角A對應的點 ( x, y ) 的坐標為：x = cosA，y = sinA

畫一個直角三角形，然後根據餘弦和正弦函數，就可以求出x和y。具體來說，就是：

cosA = = = x

cosA = = = y

換句話說，點 (x, y)等於 (cosA, sinA)。[推而廣之，如果圓的半徑為r，那麼 (x, y) = (r cosA, r sinA)。]

我們可以把上述結論推廣至任意角，把 (cosA, sinA) 定義為角A在單位圓上的對應點。（換言之，角A與單位圓交點的橫坐標與縱坐標分別為cosA和sinA。）我們用下圖來表示這個結論。

cosA與sinA的一般定義

在下圖中，我們以30°為單位，將單位圓分成若乾等分，再標記出45°的坐標，因為它們分別對應我們之前研究的特殊三角形的內角。我們列出了0°、30°、45°、60°和90°的餘弦和正弦，具體如下：

(cos 0°, sin 0°) = (1, 0)
(cos 30°, sin 30°) = (/ 2, 1 / 2)
(cos 45°, sin 45°) = (/ 2, / 2)
(cos 60°, sin 60°) = (1 / 2, / 2)
(cos 90°, sin 90°) = (0, 1)

我們還會發現，當這些角成倍擴大時，我們可以根據第一象限的情況來求其他像限角的三角函數值。

由於角的度數增加或減少360°時，角的坐標實際上沒有發生變化（只不過沿圓周運動了一圈）。因此，對於任意角，都有：

sin (A ± 360°) = sinA cos (A ± 360°) = cosA

負角的運動方向是順時針方向。例如，–30°與330°的坐標相同。請注意，沿順時針方向運動A度，與沿逆時針方向運動A度，最後的橫坐標相同，而縱坐標的正負號相反。換句話說，對於任意角 A：

cos (–A) = cosA sin (–A) = – sinA

例如，cos (–30 °) = cos 30 °= /2，sin (–30 °) = –sin 30 °= –1/2

角A關於y軸映射，就會得到補角180° –A。此時，單位圓上對應點的縱坐標保持不變，而橫坐標變成相反數。換句話說：

cos (180° – A) = – cosA sin (180° – A) = sinA

例如，當A = 30°時，從上式可知：

cos 150°= – cos 30°= – /2 sin 150°= sin 30°= 1 / 2

我們利用類似方法，繼續定義其他三角函數，例如，tan A = sinA / cosA。

x軸和y軸將平面分成4個象限，我們把它們分別稱為第一象限、第二象限、第三象限和第四象限。其中，第一象限的角為0°~90°，第二象限的角為90°~180°，第三象限的角為180°~270°，第四象限的角為270°~360°。請注意，第一象限、第二象限的正弦函數為正值，第一象限、第四象限的餘弦函數為正值，因此，第一象限、第三象限的正切函數為正值。有的學生想出了一句口訣：「All Students Take Calculus」（所有學生都要學習微積分），以首字母（A、S、T、C）對應各象限中數值為正值的三角函數（即所有三角函數、正弦、正切、餘弦）。

值得我們學習的最後一批詞彙與反三角函數有關，因為反三角函數可以幫助我們確定角的度數。例如，1 / 2的反正弦函數arc sin(1 / 2)表示角A的正弦函數sinA = 1 / 2。我們知道sin 30°= 1 / 2，因此：

arc sin(1 / 2) = 30°

反正弦函數arc sin對應的角一定在 –90°與90°之間，但我們必須知道，在這個區間之外，還有一些角的正弦函數值一樣，例如sin 150°= 1/2。同樣，在30°或150°的基礎上加上360°的倍數之後，正弦函數的值保持不變，仍然是1/2。

對於下圖所示的3–4–5三角形，利用三角函數與計算器，可以通過3種不同方法計算出角A的度數：

∠A = arc sin (3 / 5) = arc cos (4 / 5) = arc tan (3 / 4) ≒ 36.87°≒ 37°

利用反三角函數和邊長可以求出角的度數。在本例中，由於tan A = 3 / 4，因此∠A = arc tan (3 / 4) ≒ 37°

接下來，我們就可以利用這些三角函數來解決問題了。在幾何學中，給定任意直角三角形的直角邊長之後，我們就可以根據勾股定理求出其斜邊的長度。在三角學中，我們可以利用「餘弦定理」（law of cosines），對任意三角形進行類似運算。

定理（餘弦定理）：對於任意三角形ABC，已知兩條邊的邊長分別為a和b，兩邊的夾角為C，則第三邊的邊長滿足下列等式：

c2 = a2 + b2 – 2ab cos C

例如，在下圖中，三角形ABC兩條邊的邊長分別為21和26，兩邊夾角為15°。根據餘弦定理，第三邊的長度c必然滿足：

c2 = 212 + 262 – 2 (21) (26) cos 15°

由於cos 15°≒ 0.965 9，因此上述方程式可以化簡為c2 = 62.21，即c ≒ 7.89。

延伸閱讀

證明：在證明餘弦定理時，我們需要考慮∠C是直角、銳角或鈍角這三種情況。如果∠C是直角，那麼cos C = cos 90°= 0，此時餘弦定理簡化為 c2 = a2 + b2，與勾股定理一致。

如上圖所示，如果∠C是銳角，從B向畫垂線並與交於點D，就可將三角形ABC分割成兩個直角三角形。根據上圖，在三角形CBD中，由勾股定理可知 a2 = h2 + x2，也就是說：

h2 = a2 – x2

從三角形ABD可以得到 c2 = h2 + (b – x)2 = h2 + b2 – 2bx + x2，即：

h2 = c2 –b2 + 2bx – x2

綜合上面兩個等式，消去h2，可以得到：

c2 –b2 + 2bx – x2 = a2 – x2

也就是說：

c2 = a2 + b2 – 2bx

從直角三角形CBD可以得出cos C = x/a，即x = a cosC。由此可知，當∠C是銳角時：

c2 = a2 + b2 – 2ab cos C

如下圖所示，當∠C是鈍角時，我們可以在三角形的外部構建直角三角形CBD。

對直角三角形CBD和ABD分別運用勾股定理，可以得到a2 = h2 + x2，且c2 = h2 + (b + x)2。消去h2，可以得到：

c2 = a2 + b2 + 2bx

從三角形CBD可知，cos (180°– C ) = x/a，即 x = acos (180°– C ) = –acos C。因此，我們再一次證明下面這個等式成立。

c2 = a2 + b2 – 2ab cosC

順便告訴大家，我們還可以根據一個非常簡潔的公式求出上述三角形的面積。

推論：對於任意三角形ABC，已知兩條邊的邊長分別為a和b，兩邊的夾角為C，有：

三角形ABC的面積 =absin C

延伸閱讀

證明：底為b、高為h的三角形面積是bh。在證明餘弦定理時，我們考慮了三角形的3種情況。在這3種情況下，三角形的底邊都是b，因此我們現在需要確定h的值。如果∠C是銳角，通過觀察可知，sin C = h/a，即 h = a sinC。如果∠C是鈍角，有sin (180°– C) = h / a，即 h = a sin (180°– C) = a sin C，結果同上。如果∠C是直角，則h = a。由於 C = 90°，且sin 90°= 1，因此h =a sinC。也就是說，在這3種情況下，都有h = a sin C。因此，三角形的面積等於ab sin C。證明完畢。 □

根據推論，我們發現：

sin C =

因此，

換句話說，對於三角形ABC來說，(sin C) / c等於三角形ABC面積的兩倍與所有邊長乘積的商。不過，這個結論對角C沒有任何特定要求，換成(sinB) / b或者(sinA) / a，結論同樣成立。因此，我們實際上證明了下面這條特別有用的定理。

定理[正弦定理（law of sines）]：在任意三角形ABC中，如果3條邊的邊長分別為a、b、c，則有：

= =

有了正弦定理，在計算山的高度時，我們就多了一種方法。如下圖所示，我們重點考慮我們最初所在的位置與山頂之間的距離a。

利用正弦定理計算山的高度

方法5（正弦定理法）：在三角形ABD中，∠BAD = 32°，∠BDA = 180°– 40°= 140°，因此∠ABD = 8°。根據正弦定理：

兩邊同時乘以sin 32°，就會得到 a = 1 000 sin 32°/ sin 8°≒3 808英尺。同時，由於sin 40°≒ 0.642 8 = h / a，因此：

h = a sin 40°≒3 808×0.642 8 = 2 448

也就是說，山的高度約為2 450英尺，與前面的計算結果一致。

延伸閱讀

下面這個公式名叫「海倫公式」（Heron』s formula），也值得大家花時間學習。根據這個公式，我們可以求出邊長分別為a、b、c的三角形面積。如果先求出三角形的「半周長」（semi-perimeter）

s =

海倫公式就會變得十分簡單。根據海倫公式，如果三角形的邊長分別為a、b、c，那麼它的面積為：

例如，如果三角形的邊長分別為3、14、15（π的前5位數字），那麼它的半周長 s = (3 + 14 + 15) / 2 = 16。因此，三角形的面積為

通過代數運算和餘弦定理，可以推導出海倫公式。

妙趣橫生的三角恆等式

三角函數之間有很多非常有意思的關係，我們稱之為「三角恆等式」。前文中已經介紹了一些三角恆等式，例如：

sin (–A) = –sinA cos (–A) = cosA

還有一些有意思的恆等式可以推導出重要的公式，接下來我們將探討這些公式。第一個恆等式來自單位圓公式：

x2 + y2 = 1

由於點 (cosA, sinA) 位於單位圓上，因此它肯定滿足上述關係，也就是說 (cosA)2 + (sinA)2 = 1。這可能是最重要的三角恆等式了。

定理：對於任意角A，都有：

cos2 A + sin2 A = 1

到目前為止，我們一直在用字母A來表示任意角，但是這個字母本身沒有任何特殊的地方。上述恆等式也經常用其他字母來表示，例如：

cos2 x + sin2 x = 1

此外，人們還經常使用希臘字母θ：

cos2θ + sin2θ= 1

我們有時甚至不使用任何變量，例如，我們可以把它簡寫成：

cos2 + sin2 = 1

在證明其他恆等式之前，我們先利用勾股定理計算一條線段的長度。它是證明這個恆等式的關鍵，其計算結果本身也具有非常重要的價值。

定理（距離公式）：令L為點 (x1, y1) 與 (x2, y2) 之間的線段長度，那麼：

例如，點 (–2, 3) 與 (5, 8) 之間的線段長度為

根據勾股定理，L2 = (x2 – x1)2 + (y2 – y1)2

證明：如上圖所示，以點(x1, y1) 與 (x2, y2)之間的線段為斜邊畫一個直角三角形。三角形底邊的長度為x2 – x1，高為y2 – y1。因此，根據勾股定理，斜邊L滿足：

L2 = (x2 – x1)2 + ( y2 – y1)2

也就是說，。證明完畢。 □

注意，即使x2 < x1或y2 < y1，上述公式仍然成立。例如，當x1 = 5，x2 = 1時，x1與x2之間的差是4。儘管 x2 – x1 = – 4，但它的平方同樣是16，因此兩者的差是正數還是負數並不重要。

弧度、三角函數圖像與經濟週期

到目前為止，我們在討論幾何學與三角學問題時，所有角的度數都在0°~360°這個範圍內。但是，如果我們認真地觀察單位圓，就會發現360這個數字沒有什麼特別之處。古巴比倫人之所以選擇這個數字，可能是因為他們使用的是六十進制，而且這個數字與一年的天數比較接近。實際上，在數學和大多數科學領域，人們更喜歡使用「弧度」（radians）作為角的度量單位。弧度的定義是：

2π弧度 = 360°

或者

1弧度 =

對於「擁τ派」來說，由於 τ = 2π，因此：

1弧度 ==

換算成數字的話，1弧度約等於57°。為什麼弧度比度用起來更加得心應手呢？在一個半徑為r的圓上，2π弧度的角對應的弧長就是整個圓周，即2πr。如果我們把這個角分成若乾等分，我們得到的弧長就是2πr的若干分之一。具體來說，1弧度對應的弧長為2πr (1 / 2π) =r，m弧度對應的弧長為mr。總之，對單位圓而言，角的弧度與角對應的弧長相等。這非常方便！

圓的弧度為2π

在下圖的單位圓中，我們以弧度為度量單位標出了一些常用的角。

下面給出 τ 版本示意圖，供大家比較。

從上圖可以發現部分數學界人士喜愛 τ 勝過π的原因。90°是1/4個圓，換算成弧度就是 τ/4；120°是1/3個圓，換算成弧度就是τ /3。的確，人們之所以選擇 τ 這個字母，是因為它很容易讓人們聯想到「turn」（一圈）這個單詞。例如，360°表示一個圓圈，弧度是τ；60°表示1/6個圓圈，弧度是 τ /6。

此外，大家還會發現，用弧度替換度之後，三角函數的計算公式會變得簡潔許多。例如，我們可以通過下列公式來計算正弦和餘弦函數的值：

sin x = x – x3/3! + x5/5! – x7/7! + x9/9! – …

cos x = 1 – x2/2! + x4/4! – x6/6! + x8/8! – …

但是，x必須以弧度為度量單位，上述公式才成立。在微積分中，我們將發現正弦函數sin x 的導數就是其對應的餘弦函數cos x。同樣，前提條件也是x的單位必須是弧度。在畫三角函數 y = sin x 和 y = cos x 的圖像時，x通常以弧度為單位。

sin x和cos x的圖像，變量x以弧度為度量單位

由於正弦和餘弦函數具有循環的特性，因此它們的圖像每隔2π個單位就會重複一次。（「擁τ派」再得一分！）之所以如此，是因為角 x + 2π與角x其實是一回事兒。我們稱這些圖像的週期是2π。此外，如果將餘弦函數圖像向左移動π /2個單位，就會與正弦函數圖像完全重合。這是因為π /2弧度等於90°，也就是說：

sin x = cos (π /2 – x)

= cos (x – π /2)

例如，sin 0 = 0 = cos (– π /2)，sin π /2 = 1 = cos 0。

因為tan x = sin x / cos x，所以在cos x = 0時（x為π /2的奇數倍時）tan x無解。如下圖所示，正切函數圖像的週期是π。

y = tan x的圖像

綜合運用正弦函數和餘弦函數，幾乎可以為所有呈現週期性變化的函數繪製圖像。因此，在為氣溫等季節性變化、經濟數據以及聲波、水波、電波、心率等物理現象建模時，三角函數圖像都可以發揮極其重要的作用。

最後，我再表演一個魔術，將三角學與π之間的神秘聯繫展現給大家。在計算器上輸入盡可能多的5，我的計算器最多可以輸入16個5，即5 555 555 555 555 555。接下來，取這個數字的倒數，我的計算器給出的答案是：

1 / 5 555 555 555 555 555 = 1.8×10–16

按下計算器上的正弦鍵（角度模式），然後讀出得數的前幾位數字（如果前面是一串零，那麼統統忽略不計）。我的計算器上顯示的是：

3.141 592 653 589 8×10–18

你會發現這些數字（在小數點後面、這些數字前面，有17個零）正好是π的前若干位數！事實上，如果你一開始在計算器中輸入任意多個5（不能少於5個），最後的結果就是π。

通過本章的學習，我們發現三角學可以幫助我們更好地理解三角形和圓。三角函數彼此之間形成了各種各樣美輪美奐的關係，它們與數字π之間還有著千絲萬縷的聯繫。在接下來的一章，我們將會發現三角函數與另外兩個重要的數字同樣有著不可分割的聯繫。這兩個數字就是無理數e = 2.718 28…和虛數i。

[1] 作者特意使用「tan gent」（戶外運動愛好者）這個表達，目的是讓讀者聯想到「tangent」（正切）一詞。——譯者注

[2] 勾股數，也叫「畢氏三元數」。——譯者注

第9章用途多多的三角學

如何測量一座山的高度

三角學、三角形和三角函數

45 – 45 – 90三角形的邊長比是1︰1︰

30–60–90三角形的邊長比是1︰︰2

延伸閱讀

對於3 – 4 – 5三角形而言，sinA = 3 / 5，cosA = 4 / 5，tan A = 3 / 4

樹有多高？

單位圓、正弦定理與餘弦定理

單位圓上與角A對應的點 ( x, y ) 的坐標為：x = cosA，y = sinA

cosA與sinA的一般定義

利用反三角函數和邊長可以求出角的度數。在本例中，由於tan A = 3 / 4，因此∠A = arc tan (3 / 4) ≒ 37°

延伸閱讀

延伸閱讀

利用正弦定理計算山的高度

延伸閱讀

妙趣橫生的三角恆等式

根據勾股定理，L2 = (x2 – x1)2 + (y2 – y1)2

延伸閱讀

此圖可用於證明cos (A –B) = cosA cosB + sinA sinB

延伸閱讀

有用的三角恆等式

弧度、三角函數圖像與經濟週期

圓的弧度為2π

sin x和cos x的圖像，變量x以弧度為度量單位

y = tan x的圖像