
數字的美妙規律
數學學習始於數字。在我們學會數數,以及利用文字、數字和實物來表示數的概念之後,學校老師就會教我們通過加、減、乘、除等運算程序擺弄這些數字,而且這個過程會持續多年。但是,我們往往不會注意到這些數字本身就具有某些神奇的魔力,稍加研究,便會給我們帶來無窮的樂趣。
以數學家卡爾·弗裡德裡希·高斯(Karl Friedrich Gauss)小時候遇到的一個問題為例。一天,為了在自己處理其他事務時也讓學生們有事可做,高斯的老師給全班同學佈置了一個繁重的計算任務,要求他們求出從1至100的所有數字的和。結果,高斯很快就寫出了答案——5 050,讓老師和其他同學大為震驚。他是怎麼得出這個答案的呢?高斯默想著把從1至100的所有數字分成兩行,1至50按從小到大的順序位於第一行,51至100按從大到小的順序位於下面一行,如下圖所示。高斯發現,每一列的兩個數字的和都等於101,因此所有數字的總和就是50×101,等於5 050。

將1~100的數字分為兩行,每一列的兩個數字的和都為101
後來,高斯成了19世紀最偉大的數學家,這並不是因為他善於心算,而是因為他可以讓數字展現出優美的舞姿。我們將在本章探討很多有趣的數字規律,以瞭解數字是如何跳出美麗的舞蹈的。其中,有的規律可以幫助我們提高心算的速度,有的則會給我們帶來美的享受。
我們在前文中用高斯的方法計算了前100個數字的和,如果我們需要計算前17個、1 000個或者100萬個數字的和,該怎麼辦呢?事實上,我們可以利用高斯的方法,計算前n個數字的和,n可以取任意值。有人可能會覺得數字過於抽像,那麼我們可以結合圖形來表示這個過程。如下圖所示,由於1、3、6、10和15等數字可以用相應個數的小圓圈表示,這些小圓圈又可以排列成三角形,因此我們把這些數字稱作「三角形數」(triangular number)。(也許你認為一個圓圈無法構成一個三角形,但1還是被視為三角形數。)根據三角形數的定義,第n個三角形數為1 + 2 + 3 + … + n。

前5個三角形數是1、3、6、10和15
請注意觀察,如果把兩個三角形並排放置,如下圖所示,會出現什麼樣的結果呢?

在這個矩形中,一共有多少個小圓圈?
這個由兩個三角形構成的矩形共包含5行和6列小圓圈,總數為30個。因此,每個三角形所包含的小圓圈數應該是矩形的1/2,也就是15個。當然,這個結果我們早已知道。但是,上述方法表明,如果我們把包含n行小圓圈的兩個三角形放到一起,那麼所得到的矩形包含n行和n + 1列小圓圈,也就是n×(n+1)個〔通常簡寫為n(n+1)個〕。於是,前n個數字的求和公式就這樣被推導出來了:
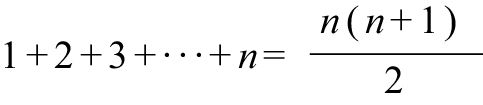
請大家回想一下這個推導過程。通過求前100個數字的和,我們找出一個規律,然後加以推廣,就可以處理同一類型的所有問題。如果要求從1至100萬的所有數字的和,只需兩步就可完成:1 000 000乘以1 000 001,再除以2!
一旦你找到了一個數學公式,其他公式常常會自動地出現在你的眼前。例如,如果我們把上述方程式的兩邊同時乘以2,就會得出前n個偶數的求和公式:
2 + 4 + 6 + … + 2n = n (n + 1)
那麼,前n個奇數的和是多少呢?讓我們看看數字會給我們哪些提示。

前n個奇數的和是多少?
等號右邊的數字都是「完全平方數」(perfect squares):1 × 1,2 × 2,3 × 3,等等。不難看出,前n個奇數的和似乎是n × n,記作n2。但是,如何確定這個結果不是一種暫時性的巧合呢?我們將在第6章通過幾種方法來推導出這個公式。不過,我們應該可以找到一個非常簡單的方法,解釋這個並不複雜的規律。我最喜歡使用的證明方法仍然是計算小圓圈的個數,這個方法還會告訴我們像25這樣的數字為什麼又叫完全平方數。前5個奇數的和為什麼是52呢?看看下圖中邊長為5的正方形,你就知道了。

正方形中共包含多少個小圓圈?
這個正方形共包含5×5=25個小圓圈。接下來,我們換一種方法來數上圖中的小圓圈的個數。我們從左上角的第一個小圓圈開始數,它依次被3個、5個、7個和9個小圓圈包圍,即:
1 + 3 + 5 + 7 + 9 = 52
如果正方形的邊長是n,我們就可以把它分成n個大小分別是1,3,5,…,(2n – 1)的L形區域(開口朝向左上角)。於是,我們得出前n個奇數的求和公式:
1 + 3 + 5 + … + (2n–1) = n2
延伸閱讀
我們將在本書後面的章節中看到,高等數學可以利用這種統計小圓圈個數的方法(以及通過兩種不同方法回答一個問題的常規做法),得出一些非常有意思的結果。不過,我們也可以借助這種方法去理解初等數學,例如,為什麼3 × 5 = 5 × 3。小時候,老師告訴我們,因數的先後次序不會影響乘積的大小(這在數學領域被稱為乘法交換律)。我相信,你們當時根本沒有懷疑它的準確性。但是,每袋裝5枚彈珠、共3袋,和每袋裝3枚彈珠、共5袋,彈珠的總數為什麼一樣多呢?數一數3 × 5的矩形中小圓圈的個數,就能理解其中的道理了。按行統計,我們看到一共有3行,每行有5個小圓圈,所以小圓圈的個數是3 × 5。但是,如果按列計算,那麼一共有5列,每列3個小圓圈,因此小圓圈的個數是5 × 3。

為什麼3 × 5 = 5 × 3?
利用奇數和的規律,我們還可以發現一個更加優美的規律。如果我們的目標是讓這些數字跳舞,那麼它們應該跳的是「方塊舞」(square dancing)。

你發現其中的規律了嗎?每行數字的個數很容易數清楚,分別是3、5、7、9、11,等等。然而,下面這個規律卻可能是大家想不到的。每行的第一個數字是多少?從前5行看,分別是1、4、9、16、25,它們都是完全平方數。為什麼呢?我們以第5行為例。在第5行之前,一共出現了多少個數字?數一數前4行的數字,共有3 + 5 + 7 + 9個。在這個和的基礎上加1,就可以得到第5行的第一個數字,所以,這個數字就是前5個奇數的和,即52。
接下來,我們不用求和的方法,證明第5個等式成立。如果高斯遇到這種情況,他會怎麼做呢?我們先不看這行的第一個數,也就是25,那麼等號左邊只剩下5個數,而且它們分別比等號右邊的5個數小5。

第5個等式左右兩邊數字的比較
因此,等式右邊5個數的和比等式左邊除25之外的5個數的和大25。但是,兩者之間的差正好被等式左邊的第一個數字25彌補了,因此等式成立。利用同樣的方法完成一些代數運算就可以證明,即使行數無限增加,這個規律也依然存在。
延伸閱讀
下面,我把這些代數運算介紹給大家,如果你不感興趣,可以略過不看。在第n行之前,有3 + 5 + 7 + … + (2n – 1) = n2– 1個數字,因此第n行的第一個數字是n2,後面有n個連續的數字,從n2 + 1至n2 + n。等式右邊有n個連續的數字,從n2 + n + 1至n2 + 2n。如果先不考慮等式左邊的第一個數字n2,就會發現等式右邊的n個數字分別比等式左邊對應的n個數字大n,因此兩者的差是n × n,即n2。如果加上左邊第一個數字n2,等式就成立了。
我們再討論另外一個規律。我們已經知道,可以利用奇數得到平方數。現在,我們把下圖大三角形中的所有奇數相加,看看得數有什麼規律。

奇數三角形
我們發現3 + 5 = 8,7 + 9 + 11 = 27,13 + 15 + 17 + 19 = 64。數字1、8、27和64有什麼共同點呢?它們都是「完全立方數」(perfect cubes)!例如,將第5行的5個數字相加,就會得到
21 + 23 + 25 + 27 + 29 = 125 = 5×5×5 = 53
這個規律似乎表明,第n行所有數字的和是n3。這是一個永恆的規律,還是一個奇特的巧合呢?為了理解這個規律,我們觀察第1、3、5行,看看每行正中間的那個數字有什麼特點。可以看到,這三個數字分別是完全平方數1、9和25。第2行和第4行的正中間不是數字,但是加號左右兩邊的兩個數字分別是3、5和15、17,它們的平均數分別是4和16。這個規律如何加以利用呢?
查看第5行我們就會發現,這5個數字關於25左右對稱。因此無須相加,我們就可以知道它們的和是53。這是因為這5個數的平均值是52,它們的和是52 + 52 + 52 + 52 + 52 = 5 ×52,即53。同理,第4行中4個數字的平均值是42,因此它們的和必然是43。通過一些代數運算(這裡不再贅述),我們就能證明第n行中n個數字的平均值是n2,它們的和是我們預期的n3。
關於立方數和平方數,我再給大家介紹一個規律吧。從13開始,將所有數字的立方數相加,這個和有什麼特點呢?

自然數的立方和肯定是一個完全平方數
自然數的立方和分別是1、9、36、100、225,等等,它們都是完全平方數。而且,這些完全平方數還具有某種特點:它們是1、3、6、10、15…的平方數,而這些數字又都是三角形數!前文中已經討論過,這些三角形數都是整數的和,因此
13 + 23 + 33 + 43 + 53 = 225 = 152 =(1 + 2 + 3 + 4 + 5)2
換句話說,前n個自然數的立方和等於前n個自然數的和的平方。現在,我們還不能證明這個結論是正確的,在第6章中我將為大家介紹兩種相關的證明方法。
又快又準的心算法
看著數字的這些規律,有人禁不住會問:「這些規律確實很有意思,但是它們有什麼用處呢?」對於這樣的問題,任何藝術家都會嗤之以鼻,因為在他們眼中,這些優美的規律本身就是一種美!大多數數學家也會有同樣的反應。而且,對這些規律的理解越深入,就越能體會其中蘊藏的美。有的規律不僅優美,還可以用來解決某些實際問題。
下面以一個我年輕時發現的簡單規律為例。這個發現讓我非常開心,儘管我並不是發現這個規律的第一人。當時,我正在求解和為20的兩個數字(例如10和10,9和11)的最大乘積。我發現,當這兩個數字都是10時,它們的乘積可能是最大的。結果,下圖揭示的規律證實了我的猜想。

和為20的兩個數字的乘積
這個規律沒有任何錯誤。隨著兩個數字之間的差不斷增大,它們的乘積卻越來越小。這些乘積與100的差是多少呢?答案是1、4、9、16、25,也就是12、22、32、42、52,以此類推。這個規律是不是始終有效呢?我決定驗證一下和為26的兩個數字是否也符合這個規律。

和為26的兩個數字的乘積
同樣,當這兩個數字相等時,它們的乘積最大,而且這些乘積與169的差依次為1、4、9,等等。在驗證了幾次之後,我確信這個規律是正確的。(我會在下文中用代數方法證明它。)然後我發現,我可以用這個規律快速地完成平方運算。
假設要計算13的平方數。我們無須直接計算13 × 13,而可以進行更簡單的計算:10×16 = 160。這個得數與正確答案已經非常接近了。由於這兩個因數與13分別相差3,因此還需要在它們乘積的基礎上加上32。即
132 =(10×16) + 32 = 160 + 9 = 169
再試一次,利用這個方法計算98 × 98。一個因數加上2等於100,另一個因數減去2等於96,在100×96的乘積基礎上加上22。即
982 =(100×96) + 22 = 9 600 + 4 = 9 604
如果某個數的個位數是5,進行平方運算時就會特別簡單,因為該數字分別加、減5之後,兩個因數的個位數都是0。例如:
352 =(30×40) + 52 = 1 200 + 25 = 1 225
552 =(50×60) + 52 = 3 000 + 25 = 3 025
852 =(80×90) + 52 = 7 200 + 25 = 7 225
現在,試試看如何計算592。因數59分別加、減1之後,算式就變為:592 = (60 × 58) + 12。但是,60 × 58怎麼心算呢?答案是:由左至右。先忽略60後面的那個0,用從左至右的方法計算6 × 58:6 × 50 = 300,6 × 8 = 48。然後,把這兩個數字(從左至右)相加,得到348。因此,60 × 58 = 3 480。那麼
592 =(60×58) + 12 = 3 480 + 1 = 3 481
延伸閱讀
下面,我們通過代數運算來解釋其中的道理。(在你讀完第2章關於平方差的內容之後,再回過頭來看這部分內容,效果可能會更好。)
A2 = (A + d) (A–d) + d2
其中A是平方運算的底數,d是A與離其最近的簡便數字的差(當然,d取任意值時,上述公式都成立)。例如,計算59的平方數時,A = 59,d = 1。根據公式,計算(59 + 1)×(59–1) + 12就可以得出答案。
在你對兩位數的平方運算感到得心應手之後,還可以利用這個方法完成三位數的平方運算。例如,如果我們知道122 = 144,那麼
1122 = (100×124) + 122 = 12 400 + 144 = 12 544
如果乘法運算中的兩個因數都與100接近,就可以利用類似方法完成計算。第一次看到這個方法時,大家都會覺得它很神奇。以104×109為例。如下圖所示,我們在每個數字旁邊寫上該數字與100的差。然後,將第一個數字與第二個差相加,即104 + 9 = 113。再將兩個差相乘,即4×9 = 36。最後,將這兩個運算步驟的得數寫到一起,答案就會神奇地出現在你的眼前。

計算兩個接近100的數字乘積的神奇算法(以104×109 = 11 336為例)
第2章將進一步介紹類似的例子,並利用代數方法討論其中的道理。不過,既然提到心算,我就多說幾句。我們花了大量時間學習紙筆計算,但在心算方面投入的時間卻很少。然而,在大多數現實情況下,我們需要的可能不是紙筆運算能力,而是心算能力。對於數額較大的運算,我們大多會用計算器得到確切答案,但在看營養成分表或者聽演講、銷售報告時,我們通常不會掏出計算器,而是在心裡對某些重要數字進行大致的估算。學校教給我們的那些方法往往只適用於紙筆運算,而心算效果通常不是很好。
各種快速心算的方法可以寫成一本書,但我在這裡僅介紹一些最基本的策略。我覺得需要再三強調的一個做法是從左至右計算。心算是一個不斷追求簡便化的運算過程。遇到一個難題時,我們應該把它轉化成多個比較簡單的問題,直到最後得出答案。
加法心算
請思考下面這道題:
314 + 159
(我用橫式給出這道題,目的是不讓你進入紙筆運算模式。)先在314的基礎上加上100,以降低題目的難度:
414 + 59
在414的基礎上加上50,以進一步降低難度,使它變成我們可以輕鬆解決的問題:
464 + 9 = 473
以上就是加法心算的本質所在。除此之外,我們偶爾還會採用的一個有效方法,就是把較難的加法問題變成較簡單的減法問題。在計算零售商品的價格時,我們經常需要採用這個方法。例如,請計算:
23.58美元 + 8.95美元
8.95美元比9美元少5美分,因此我們可以先在23.58美元的基礎上加上9美元,再減去5美分。通過這個方法,這道難題就變簡單了:
32.58美元 – 0.05美元=32.53美元
減法心算
做減法心算時,最常用的重要策略是增大減數。例如,當減數是9時,更簡單的方法是先減去10,再加上1。例如:
83 – 9 = 73 + 1 = 74
再例如,當減數是39時,先減去40,再加上1的計算方法可能會更簡便。
83 – 39 = 43 + 1 = 44
如果減數是兩位以上的多位數,心算時就需要使用一個非常重要的概念——「補數」(complements)。某個數的補數是這個數與它最近的「約整數」(round number)之間的差。一位數的補數就是該數與10之間的差,例如,9的補數是1。兩位數的補數是該數與100的差。下面是幾組和為100的數字,能看出其中有什麼特點嗎?

互補的兩位數相加,和為100
我們說87的補數是13,75的補數是25,以此類推。反之,13的補數是87,25的補數是75。從左至右仔細研究這5道題,就會發現所有題目(最後一道題除外)中最左邊的數字相加等於9,最右邊的數字相加等於10。只在兩個數字的個位數都是0(例如,最後一道題)時,才會出現例外結果。例如,80的補數是20。
請利用上述方法計算1 234 – 567的得數。在進行紙筆運算時,這道題不會讓人覺得多有意思。但是,如果利用補數來計算,就會把比較難的減法問題變成比較容易的加法問題!當減數是567時,我們先減去600。這個運算不難,如果從左至右思考,就更簡單了:1 234 – 600 = 634。但是,你把減數變大了,大了多少呢?想一想,567與600相差多少?這與67和100的差是一樣的,都是33。
1 234 – 567 = 634 + 33 = 667
請注意,這道加法題特別簡單,因為它不涉及「進位」(carries)。利用補數做減法計算時,通常都不需要進位。
三位數的補數也有類似特點。

互補的三位數相加,和為1 000
在大多數情況下(個位數不是0),兩個互補的三位數對應數位上的數相加之和是9,但最後一位數字相加之和是10。以789和211為例,7 + 2 = 9,8 + 1 = 9,9 + 1 = 10。在找零錢時,運用這個方法就會非常方便。例如,我從附近熟食店買的三明治價格是6.76美元。如果我付給收銀員10.00美元,他應該找給我多少錢呢?計算過程十分簡單,就是找到676的補數,即324。因此,熟食店應該找給我3.24美元。
延伸閱讀
我每次買這種三明治時,都會情不自禁地想到它的價格與找零竟然都是完全平方數(262 = 676,182 = 324)。(給大家出一道附加題:還有兩個數字的完全平方數之和也正好是1 000,你能找到它們嗎?)
乘法心算
記住10以內的乘法表之後,就可以利用心算得出所有乘法問題的答案,至少是一個近似答案。接下來,我們需要掌握(無須死記硬背)一位數與兩位數乘法問題的解法,其中的關鍵是從左至右計算。例如,求8×24的得數時,應該先計算8×20,然後再加上8×4的乘積:
8×24 = (8×20) + (8×4) = 160 + 32 = 192
熟練掌握這個方法之後,就可以用心算解決一位數與三位數的乘法問題了。這類問題的難度有所增加,因為需要記憶的信息增加了。其關鍵是在計算過程中一步一步地完成加法運算,以免需要記憶太多的數字。例如,在求456×7的積時,如下圖所示,先求2 800 + 350的和,再加上42。

掌握了一位數與三位數的乘法心算之後,就可以著手解決兩位數與兩位數的乘法問題了。在我看來,這樣的題目才有點兒意思,因為通常來說,你可以用不同的方法解決這些問題,檢驗答案是否正確,還可以享受快速找到答案的喜悅之情!下面,我通過計算32×38,向大家介紹這些方法。
大家最熟悉的方法(與紙筆運算最接近的一種方法)是加法,該方法適用於解決所有乘法問題。首先,把其中一個因數(通常是位數較少的那個因數)分成兩個部分,然後這兩個部分分別與另一個因數相乘,最後將乘積相加。例如:
32×38 = (30 + 2)×38 = (30×38) + (2×38) = …
那麼,如何計算30×38呢?先計算3×38,然後在乘積的後面添加一個0。由於3×38 = 90 + 24 = 114,因此30×38 = 1 140。再計算2×38 = 60 + 16 = 76,因此:
32×38 = (30×38) + (2×38) = 1 140 + 76 = 1 216
計算這類問題(尤其當其中一個因數的末位是7、8或者9時)的另一種方法是減法。在這個例子中,我們要用到38 = 40 – 2,那麼:
38×32 = (40×32) – (2×32) = 1 280 – 64 = 1 216
用加法和減法求兩位數與兩位數的乘積時,我們需要記住一個較大的數字(例如,這個例子中的1 140和1 280),還要進行其他運算。這對我們來說是一個比較難的挑戰。通常,我喜歡用「因數分解法」(factoring method)來計算兩位數與兩位數的乘積。只要其中一個因數可以表示成兩個一位數乘積的形式,就可以採用這種方法。例如,我們發現32可以分解成8×4,因此:
38×32 = 38×8×4 = 304 × 4 = 1 216
如果我們把32分解成4×8,上述運算就會變成38×4×8 = 152×8 = 1 216。不過,我喜歡先用較大的因數去乘以剩下的那個兩位數,這樣一來,最後與這個乘積(常常是一個三位數)相乘的就是那個較小的因數了。
延伸閱讀
在一個因數是11的倍數時,因數分解法可以起到很好的效果。在這種情況下,有一個特別簡單的巧妙算法:在另一個因數的兩個數位中間插入這兩個數位上的數字之和,就可以得到你所求的乘積。例如,計算53×11時,因為5 + 3 = 8,因此最終的乘積就是583。27×11呢?因為2 + 7 = 9,因此答案是297。如果兩個數字之和大於9,怎麼辦?在這種情況下,我們插入和的個位數,然後在第一個位數上加1。例如,由於4 + 8 = 12,因此48×11的答案是528。同理,74×11 = 814。如果一個因數是11的倍數,就可以利用上面這個巧妙的辦法。例如:
74×33 = 74×11×3 = 814 × 3 = 2 442
兩位數乘法問題的另外一個有趣的解法叫作「就近取整法」(close together method)。當相乘的兩個數字的首位數相同時,就可以使用這個方法。第一次接觸它時,你會覺得它十分神奇。比如,下面這個例子會不會讓你難以置信?
38×32 = (40×30) + (8×2) = 1 200 + 16 = 1 216
當兩個數字個位數的和為10時(例如38×32),計算起來尤為簡單。(在38×32中,兩個數的十位數都是3,個位數的和為8 + 2 = 10。)再舉一例:
83×87 = (80×90) + (3×7) = 7 200 + 21 = 7 221
即使個位數的和不等於10,計算起來也不難。例如,在計算41×44時,可以將較小的那個數減去1(得到約整數40),然後將較大的那個數加上1,於是:
41×44 = (40×45) + (1×4) = 1 800 + 4 = 1 804
計算34×37時,如果把34減去4(得到約整數30),與它相乘的數就會變成37 + 4 = 41,再加上4×7:
34×37 = (30×41) + (4×7) = 1 230 + 28 = 1 258
順便告訴大家,前面介紹的104×109這道題的神秘算法只是本方法的一個應用而已。
104×109 = (100×113) + (4×9)= 11 300 + 36 = 11 336
有的學校要求學生背誦20以內的乘法表。使用上述方法,無須背乘法表,也可以快速算出答案。例如:
17×18 = (10×25) + (7×8) = 250 + 56 = 306
這個神奇的方法為什麼有效呢?要回答這個問題,需要進行一些代數運算,我將在第2章做介紹。一旦學習了代數運算之後,我們就能找出新的計算方法。例如,17×18還可以這樣解答:
18×17=(20×15)+〔(–2)×(–3)〕=300+6=306
說到乘法表,請仔細研究下面列出的一位數乘法表。高斯年少時應該會對這個問題感興趣:這張乘法表中所有數的和是多少?請認真思考,看能不能找出一個簡便的計算方法,我將在本章結尾揭曉答案。

該乘法表中全部100個數字的和是多少?
除法心算
首先,我們看一個答案非常簡單但在學校裡不大可能學到的問題:
(1)如果兩個三位數相乘,你能立刻說出乘積是幾位數嗎?
以及相關問題:
(2)一個四位數與一個五位數相乘,乘積可能是幾位數?
我們花費了大量時間學習多位數的乘法和除法問題,但幾乎沒有考慮過答案有哪些重要特點。而且,瞭解答案的大致範圍,比知道答案的最後一位數甚至首位數都重要得多。(知道答案的首位數是3,這毫無意義,除非你還知道這個答案更接近於30 000、300 000或3 000 000。)問題(1)的答案是五位數或六位數。為什麼?因為符合條件的最小乘積是100×100 = 10 000,它是一個五位數。最大乘積999×999的答案肯定比1 000×1 000 = 1 000 000小,但只小一點兒。1 000 000是最小的七位數,因此999×999肯定是六位數。〔當然,你也可以通過心算,很便利地算出最終得數:9992 = (1 000×998) + 1 = 998 001。〕也就是說,兩個三位數的乘積肯定是五位數或六位數。
問題(2)的答案是八位數或九位數。為什麼?最小的四位數是1 000,也可以記作103(1後面有3個0);最小的五位數是10 000= 104。因此,一個四位數與一個五位數的最小乘積是103×104 = 107,它是一個八位數。〔107是怎麼得到的?103×104 = (10×10×10)×(10×10×10×10) = 107。〕而一個四位數與一個五位數的最大乘積只比104×105 = 109這個十位數小一點兒,因此最後得數最多是九位數。
根據上述分析,我們得出一個非常簡單的規則:一個m位數與一個n位數相乘,乘積的位數為m + n或者m + n – 1。
通常,只需要看每個數字的首位數(最左邊的那個數),就可以判斷出乘積的位數。如果兩個數字首位數的乘積是10或者大於10,那麼它們的乘積肯定為m + n位數。(以271×828為例,它們首位數的乘積是2×8 = 16,因此答案是六位數。)如果首位數的乘積是4或者小於4,答案就是m + n – 1位數。(例如,314×159的乘積為五位數。)如果首位數的乘積是5、6、7、8或9,則需要仔細思考。(例如,222×444的乘積是五位數,但234×456的乘積是六位數。這兩個得數都非常接近100 000,這是其位數不易確定的一個重要原因。)
把上述規則反過來,可以得到一個更簡單的除法規則:一個m位數被一個n位數除,商的位數是m – n或者m – n + 1。
例如,一個九位數被一個五位數除,得數肯定是四位數或者五位數。判斷到底哪個答案正確的規則,甚至比乘法問題的相關規則還要簡單。在這裡,我們無須對首位數進行乘法或者除法運算,而是對兩個首位數進行比較即可。如果第一個數字(被除數)的首位數比第二個數字的首位數小,答案就是小的那個選項(m – n)。如果第一個數字的首位數大於第二個數字的首位數,答案就是大的那個選項(m – n + 1)。如果兩個數字的首位數相同,就需要比較第二個數位上的數字,具體過程同上。例如,314 159 265被12 358除時,商是五位數;但它被62 831除時,商則是四位數。161 803 398被14 142除時,商是五位數,因為16大於14。
除法的心算過程與紙筆運算比較相似,我在這裡就不贅述了。(利用紙筆做除法運算時,計算次序一定是從左至右,直到最後得出答案!)但是有時候,一些捷徑可以為我們提供便利。
除數是5(或者個位數是5的任何數字)時,將分子、分母同時乘以2,通常會降低計算的難度。例如:

在分子、分母同時乘以2之後,你也許會發現246和9都可以被3整除(我們將在第3章詳細討論這方面的內容),於是,將分子、分母同時除以3,可以進一步簡化計算。
延伸閱讀
看一下從1到10的數字的倒數:
1 / 2 = 0.5,1 / 3 = 0.333…,1 / 4 = 0.25,1 / 5 = 0.2,
1 / 6 = 0.166 6…,1 / 8 = 0.125,1 / 9 = 0.111…,1 / 10 = 0.1
我們發現,以上小數要麼在小數點後兩位處結束,要麼無限循環下去,只有1 / 7例外,它是在小數點後第7位處開始循環的:
1 / 7 = 0.142 857 142 857 …
(除了7以外,從2到11的所有數字的倒數都不長,這是因為這些數可以整除10、100、1 000、9、90或者99,而可以被7整除且具有這種特點的最小數字是999 999。)把1 / 7的各個小數項填到圓裡,神奇的一幕就會出現在我們眼前:

「七分之幾」圓
令人吃驚的是,從圓上的某個點開始,順時針循環下去,就可以得到分母是7的所有分數的數值,具體如下:
1 / 7 = 0.142 857 142 857…,2 / 7 = 0.285 714 285 714…,
3 / 7 = 0.428 571 428 571…,4 / 7 = 0.571 428 571 428…,
5 / 7 = 0.714 285 714 285…,6 / 7 = 0.857 142 857 142…。
在結束本章之前,我來回答一下前文提出的那個問題:把乘法表中所有的數字加到一起,和是多少?同計算前100個數的和一樣,這個問題乍一看也非常難。但是,只要我們熟悉了數字之舞呈現出來的令人驚歎的規律,就可以完美地解答這個問題。
我們先將乘法表中第一行的所有數字相加。高斯(或者我們前面見過的三角形數公式,甚至直接相加的方法)肯定會告訴我們:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55
第二行所有數字的和呢?算起來也非常簡單:
2 + 4 + 6 + … + 20 = 2 × (1 + 2 + 3 + … + 10) = 2×55
同理,第三行的和是3×55。因此,我們知道乘法表中所有數字的和是:
(1 + 2 + 3 + … + 10)×55 = 55×55 = 552
通過心算,我們知道答案是3 025!
