我們，是通過螺旋來到這個世界的。
但是，我們原本，是屬於地球的。
——萩尾望都 1《馬賽克·螺旋》
1萩尾望都，生於 1949 年，日本漫畫家，女子美術大學客座教授，代表作有《天使心》與《波族傳奇》等。——譯者注
9.1 
弧度
9.1.1 不高興的尤里
星期六。
我跟尤里在我家餐桌前吃著鹹仙貝。
我媽一邊倒著茶一邊說道：
“話說回來，之前在遊樂場，米爾嘉她……”
我媽這句話讓尤里一下挺直了身子。
“遊樂場？米爾嘉大人？”尤里看看我，又看看我媽。
“上次我們出去玩兒來著。”我說道。
“你都沒跟我說！米爾嘉大人跟哥哥，兩個人去的？”
我媽感覺氣氛很不妙，一下子躲回了廚房。
媽，你不要扔了個手雷就開溜啊……
“你說……為什麼不把人家也帶上？”
“那下次我們一起去玩唄。”我說道。
“……不相信你。”尤里拿懷疑的眼光瞪著我。
就這麼你一句我一句地說著說著，尤里的話慢慢地變少了。我回到了自己屋裡，她也默不作聲地跟了進來。
這是一個循環。
尤里板著臉，一直不說話。
“有什麼不滿就說出來唄。”我說道。
“……”
“你不說我哪知道啊。”
“……”
“你就自己鬧彆扭去吧。”我轉過身面向桌子。
“……”
尤里沉默著，用雙手來回搖晃著我的椅子。
我深深歎了口氣，轉頭看向她。
然後又回到了“循環”的狀態。
我跟尤里之間的這種毫無成果的交流持續了約 20 分鐘。
對於這種來來往往沒有上限的循環，我徹底認輸了。真沒辦法呀。
“是我不好，沒經你同意就去遊樂場玩兒，對不起。”
我為什麼非得道歉啊。
“……”她瞟了我一眼。
“啊，對了，”我想起一件好事兒，“米爾嘉正在考慮春假的活動呢。還記得不，說是要講我們以前說過的那個‘哥德爾不完備定理’。她讓我也把你叫上。”
“……真的？”
喲，上套了。
“真的真的。她肯定是跟我們講哥德爾不完備定理。”
“唔……那我就看在米爾嘉大人的份上原諒你吧。”
尤里神氣十足地點點頭。
唉……真是讓人哭笑不得，女生還真麻煩啊。
9.1.2 三角函數
“哥哥，我想讓你教我 sin 和 cos 喵！”
她突然換成了撒嬌般的貓語。
“可以倒是可以……你課上學到了？”
“老師在課上的剩餘時間裡，講了一點正弦曲線。不過我沒聽明白。”
“原來如此。”
“放了學，我找喜歡數學的朋友問了，不過還是沒明白。那傢伙講到最後總是發脾氣，然後就不說了。人家說沒明白，他卻反過來怪人家……我們總是吵架。”
“哦……”
“還是哥哥你最好了！所以說，sin、cos ！”
“好，好。”
我一翻開筆記本，尤里就從胸前口袋裡拿出眼鏡戴上了。
“說得簡單點哈。”
“我用單位圓來講吧。單位圓就是半徑為 1 的圓。”
我畫了一個以原點為中心的單位圓。
“單位圓。”尤里複述道。
“假設圓周上存在一點 P，我們把下圖裡的這個角度稱為 θ，讀作‘西塔’。”
“西塔？”
“θ 是一個希臘字母。不過，現在我們只要把它當成一個表示角度的字母就行了。表示角度的時候經常會用到它。”
“知道了，你說它叫西塔，那就叫西塔吧。”
“點 P 在圓周上運動的時候，角 θ 會隨之變化，對吧？”
“是這樣。”
“相應地，點 P 的 y 坐標也會發生變化。”
“這個當然啦。因為點 P 的 y 坐標是 P 的高度嘛。”
“如果 θ 的實際度數能確定，那麼 y 的數值也就能確定。”
“嗯，能確定，能確定。”
“當點 P 在單位圓的圓周上運動時，y 的值會隨著 θ 的變化而發生什麼樣的變化呢？我們把這種‘表示 θ 與 y 的對應關係的函數’叫作 sin 函數。”
“誒？這就是 sin、cos 的 sin ？”
“沒錯。如果 θ 能確定，那麼點 P 的 y 坐標也就能確定。我們把這個 y 寫成下面這樣。”
y = sin θ
“y 等於 sin θ。根據角 θ 來確定 y ？”
“沒錯。”
“哦哦……原來這麼簡單呀。”
“就是這麼簡單啊。”
9.1.3 sin 45°
“那 cos 是什麼呢？”
“在談 cos 之前，我們來研究一下 sin 的具體值。比方說，當 θ 為 0°的時候，sin θ 是多少？”
“嗯……應該是 0 吧？”尤里想了想回答道。
“沒錯。因為當 θ 等於 0°時，y 等於 0。”
“是呢。點 P 在 x 軸上嘛。”
“對。也就是說，sin 0° = 0。”
“人家已經明白了啦。”
“當 θ 等於 90°時，y 等於 1。”
sin 90° = 1
“這個時候，點 P 在圓的最上方，是吧？”
“沒錯。在這裡，我們假設 θ 從 0°到 360°轉了一圈，此時 sin θ，也就是 y，會在什麼範圍內移動呢？你知道嗎？”
“y 會在 0 跟 1 之間移動……啊，不對！還有負數呢！”
“嗯嗯。”
“因為是‘咻’地一下上去再‘咻’地一下下來，所以 y 的值在 1 跟 -1 之間。”
-1 ≤ sin θ ≤ 1
“沒錯。sin 270°是 -1，sin 90°是 1。”
“人家都說已經明白了啦！”
尤里的語氣裡透出些許焦躁。她解開馬尾辮，重新紮好頭髮。咦，尤里的頭髮還真是長啊。
“……那你知道 sin 45°是多少嗎？”我問道。
“誒？它是 sin 90°的一半，所以是 
吧？”
“不是哦。你從剛才那張圖裡找找 θ = 45°的情況看一下。”
“嗯嗯……啊，y 要比 稍微大一點喵！”
“尤里你的話，應該能精確求出 sin 45°的！”
“要用類似量角器的工具嗎？”
“不不，用計算來求。你想像一下正方形的對角線就行了。”
“嗯……是對角線的長度為 1 的正方形的……邊長？”
“對，這就是 y ！你的答案是？”
“嗯……
，不對，是 
。”
“你是怎麼算的？”
“不就是這個數嗎？”尤里說道。
“是沒錯啦。利用勾股定理……”
“呃……我不是那麼算的。”尤里說道，“如果正方形的邊長為 1，對角線不就是 
麼？要想把對角線變成 1，拿整個正方形除以 就行了。這樣正方形的邊長就會變成 
，對吧？給分子分母同時乘以 ，就得 。”
“嗯，這樣也可以的。對了， 約等於 1.4 哦。”
“為什麼？”
“因為把 1.4 平方，就是 1.42 =1.96。也就是說，1.42 約等於 2。”
“喔喔。”尤里點點頭。
“所以， 約是 1.4 的一半，約等於 0.7。”
“喔喔，原來如此。”
“這樣一來，我們就能求出 sin 45°的值了，它約等於 0.7。”
“噢，原來如此……”
“再精確點的值就是 
，我們可以這麼寫。”
“喵來如此。原來我們能自己計算出 sin 45°啊。”
9.1.4 sin 60°
“那你知道 sin 60°是多少嗎？”我問道。
“這個……就是求下面這個 y 唄。”
“對對。你注意到什麼沒有？”
尤里認真地盯著圖看。
她用指頭撓了撓鼻尖，自言自語說了句“不對……”。
尤里越來越不服輸了啊。
“是這樣的，對吧？我明白了。”
尤里抬起頭。圖上多畫了兩個點 —— A 跟 Q。
“喔，挺好的嘛。”
“這是正三角形，對吧？”
“沒錯。△POA 是正三角形。因為邊 
跟邊 
是圓的半徑，所以長度相等。也就是說，∠OPA 跟∠OAP 相等。又因為∠POA 等於 60°，而三個角∠OPA、∠OAP、∠POA 的和是 180°，所以到頭來三個角都是 60°，因此是正三角形。”
“對對。”尤里說道，“所以，嗯……如果從上面的頂點 P 筆直地向下引一條直線，就能構成直角三角形 △POQ。然後，因為邊 
是邊 的一半，所以是 。因此 y 的值取 
的平方根……”
尤里往筆記本的一角凌亂地列著式子，計算著。
“我明白了。
！”
“嗯，很好。因為 
約等於 1.7，所以 sin 60°約等於 0.86。”
“我們能知道精確的值麼？”尤里問道。
“再精確點的值就是 
，我們可以這麼寫。
……不過，尤里，你在筆記本上計算的時候把式子寫開一點，別寫得那麼擠，在本子角落裡寫得密密麻麻得可不行。”
“噢……”
“我說的這點很重要啊。——然後，我們就能馬上得出 sin 30°的值了。”
“誒？為什麼？啊！明白了，明白了！把正三角形放倒，用 90°- 60° = 30°不就行了嘛。哥哥，sin 30°的值是 吧？”
“嗯，很好。這樣我們就知道 θ 分別為 0°, 30°, 45°, 60°, 90°時的 sin θ 的值了。當角度超過 90°時，我們就要利用 對稱性。”
“不明白什麼意思。對稱性？”
“因為圓是左右對稱的，所以 sin 120°等於 sin 60°。看了下面這張圖，你肯定就會明白意思了。”
“嗯……喔，這樣啊。P 的 y 坐標等於 P' 的 y 坐標……也就是說，sin 120°等於 sin 60°，對吧？原來如此。那剩下的不就都能求出來了嗎？超過 180°的話，加上個負號就行了。”
“對對。”
我又重新畫了張圖，將那些能馬上求出 sin 值的點標注在了圓上。
9.1.5 正弦曲線
“喂喂，話說，還不講正弦曲線呀？”
“誒？你以為我們是為了什麼才計算 sin θ 的？”
“為了什麼啊？”
“為了畫正弦曲線。我們列個 θ 跟 sin θ（即 y）的關係表吧。”
“喔喔。”尤里點點頭。
“超過 180°以後，加個負號就行了。”
“嗯嗯。”
“然後，sin 360°就會回到 0。你看出正弦曲線了沒？”
“怎麼回事？”尤里問道。
“這麼回事。”我畫了張圖，把各個點標注了出來。
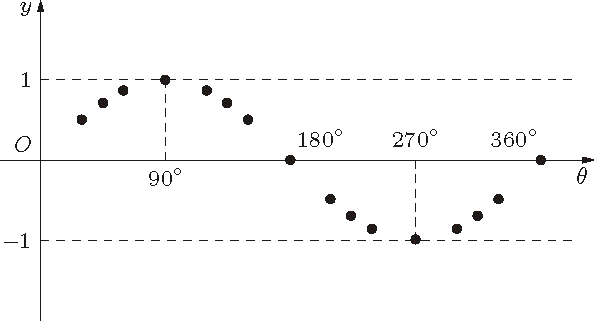
標注出 (θ, sin θ) 的點
“噢！噢噢！這是……”尤里探出身子。
“對對。把這些點流暢地連接起來的話……”
“人家來連！”
正弦曲線
“就是這樣。”我說道。
“正弦曲線出來了……咦？不好意思哥哥，我不明白。雖說剛才我們畫的單位圓跟這個正弦曲線形狀不一樣，不過我想問一下，它們是同一個圖嗎？”
“尤里你把看圖的基本方法給忘了麼？看圖的時候要注意數軸。剛剛我們畫單位圓的時候，橫軸是 x，縱軸是 y，因此這個單位圓表示的是 x 跟 y 的關係。在我們剛剛畫的正弦曲線裡，橫軸是 θ。正弦曲線表示的是 θ 跟 y 的關係，也就是說，是下面這樣。”
- 單位圓是將點 P 的運動看作是“x 和 y 的關係”而畫的圖
- 正弦曲線是將點 P 的運動看作是“θ 和 y 的關係”而畫的圖
“原來如此喵！正弦曲線……我好像明白一點了。”
“那就好。”我點點頭。
“有一點我很在意，就是在單位圓的圖上能看得到 x, y, θ，但是在正弦曲線的圖上就只能看到 θ 跟 y ——算了，先不說這個。那個……哥哥。”
尤里慢慢摘下眼鏡，把眼鏡腿疊好。
然後，她字斟句酌地開口道：
“那個……哥哥，人家還明白了一件事。這件事跟數學無關，跟我自己有關。哥哥，我好像太著急往前趕了。比如剛剛，我聽完了 sin 就馬上想聽 cos……我總是著急忙慌地想往前趕。”
“著急忙慌？”
“嗯……怎麼說呢，要是我能‘唰唰’地理解，就會想‘我明白啦，往下講吧’；要是我不能‘唰唰’地理解，就會想‘麻煩死了，別再講啦’。可是，哥哥你不一樣，你一直不慌不忙的。”
“沒必要著急呀。因為數學是經過成百上千年才發展到現在這個樣子的。各個時代最傑出的人物絞盡了腦汁呢……在現在的數學書上寫著的符號、式子和思路產生之前，數學家們應該是在一條我們無法想像的漫長道路上煎熬著。所以，我們一下子看不明白也不要緊。倒不如說，不明白可能更好。”
“不明白也行嗎？”
“比感覺自己明白了強得多。也就是說，懂得‘這本數學書上寫的內容可能是這個意思，不過實際上，我自己可能並沒有搞明白’就行。”
“就是說持續燃燒下去的愛情，要比劇烈燃燒卻立即消失的戀情更重要唄。”
“你在說什麼？”
“先不說這個，趕緊給人家講 cos 嘛～”
“sin 是 θ 和 y 的關係，對吧？ cos 就是 θ 和 x 的關係。”
“喔……”
“接下來你就自己研究看看吧。”“呵呵，哥哥你可真夠意思。”
y = sin θ 和 x = cos θ 的關係
9.2 
弧度
9.2.1 弧度
“……就這樣，我給尤里講了正弦函數。”我說道。
“sin、cos…… 我對三角函數特別頭疼。”泰朵拉說道。
現在是午休時間。我跟泰朵拉在天台上吃著午飯，晴空萬里。明天是結課典禮，後天就開始放春假了。
“是嗎？我還以為你理解得很透徹呢。”
“有些地方的確是理解了，但是說不上‘完全理解’……”
“不不，就算是數學家也沒人敢說‘完全理解’呀。”
“那個……我有一種‘實際上，我並沒搞明白’的感覺。”
“比如說呢？”
“比如說，在學三角函數之前學過的弧度……”
“哦哦。”
“弧度是角度的單位，對吧？ 90°等於弧 
度，180°等於 π 弧度，360°等於 2π 弧度……這些我已經理解了。我也明白弧度跟度成比例。可是……話說回來，為什麼 360°等於 2π 弧度呢？說真的，我不明白。”
泰朵拉像轉動儀表盤的指針似地，把筷子轉了一圈。
“根據‘圓弧的長度是半徑的多少倍’去思考弧度，就會很簡單。”
“圓弧的長度是半徑的多少倍？”
“對。比如說，假設我們需要思考 360°是多少弧度。如果設圓的半徑為 r，那麼與 360°對應的圓弧 —— 整個圓周 —— 的長度會是多少呢？”
“半徑為 r 的圓周的長度是……嗯，是 2πr。”
“嗯。那 2πr 是半徑 r 的多少倍呢？”
“因為是用 2πr 除以 r，所以得 2π 倍 ——啊！所以是 2π弧度？”
“沒錯。弧度是用‘圓弧的長度’去測量‘角度的大小’。但是，如果圓的半徑變成原來的兩倍，那麼雖然角度不變，但是圓弧的長度卻會變成原來的兩倍。因此，我們才通過‘圓弧的長度是半徑的多少倍’，換言之就是‘圓弧的長度與半徑的比’來表示角度。”
“為什麼不能用 360°呢？”
“一圈用 360°可能是因為 360 的約數多。倒不是不能用……就是顯得有些隨便。因為 360 這個數是人為規定的。與其相比，用圓弧的長度與半徑的比來表示角度就更為自然一些……不過這種表示方法也是人為規定的。”
“瞭解。”
“中心角在圓上形成的圓弧的長度。這個圓弧的長度與半徑的比所表示的角度就是弧度。比如說在半徑為 r 的圓上，60°形成的圓弧計算如下。
是半徑的 
倍，對吧？因此，60°等於 弧度。”
我拿出筆記本，畫了張圖。
60°等於 弧度
“啊，我有點明白了。”泰朵拉說道。
9.2.2 教人
泰朵拉吃完飯，拿粉色的手帕把便當盒包了起來。
我把裝麵包的袋子塞到口袋裡，站起身伸了個懶腰。
“最近啊，我朋友總問我數學……”她說道。
“嗯。教別人也能提升自己呢。”
“不過，我解釋得不太順，最後人家總會給我一句‘還是算了吧。’”
“噢。”我說道。
“自己學習跟教別人，看起來很像，實際上卻天差地別。”泰朵拉說道，“老師們真不容易呀……原來我還很不滿，覺得‘這是什麼啊，能不能講明白點呀’，現在才知道教人原來這麼不容易呀，更何況還是教一群人。”
“對啊。”
“我覺得學長你很會教人，很了不起。”
“可是，我也教不了一群人啊。泰朵拉你在聽我講的時候，會經常問一些問題，比如‘這裡我不明白’。你問的問題可幫了我大忙呢。沒有這些問題，我就得一邊想著‘她明白了沒有啊’一邊往下講。”
可是……我開始獨自思考。
可是，如果今後我更深入地研究數學，教人會不會變得非常難呢？隨著不斷接近數學的本質，剛從山裡挖出的原石、剛從海中撈上來的貝殼或是剛摘下來的果實……這樣的東西不就會越來越多嗎？雖然我不知道它們真正的價值，但它們是那麼美麗，那麼充滿生機。我能把這些教給別人嗎？
“學長？”
“啊，抱歉，我有點走神。”
泰朵拉撥弄著用手帕打出來的結，開口說道：
“那個……我很慶幸自己能來這所高中上學。”
“是嗎，那很好啊。”
“那個……我很慶幸自己來了以後，馬上就給學長你寫了信。”
“嗯，我也覺得很高興啊。”
“那個……我……我……”
下午課的預備鈴響了。
“那個，那個，那個……學長還要再跟我一起吃午飯哦。”
9.3 
弧度
9.3.1 停課
我剛回到教室，就碰見米爾嘉站在教室門口。
“我們下午停課。”
“為什麼啊？”
我一頭霧水地被她拉著出了學校。
米爾嘉走得很快，我跟在她身後。我們穿過大道，走過十字路口。在反常的時間走平常上學時走的路，感覺有些奇怪。
到了車站，我們乘上電車，並排坐下。
9.3.2 餘數
電車沐浴在溫暖明媚的日光下，緩緩前行。這是要去哪兒呢？
“這不是停課……是逃課吧？”我說道。
“午休那會兒，你去哪裡了？”米爾嘉擦拭著眼鏡衝我問道。
“天台。”
“喔……”她重新戴好眼鏡，看著我的眼睛。
“我跟泰朵拉吃午飯來著。”我迅速說道。
“泰朵拉是個好女孩兒，對吧？”米爾嘉說道。
“我們聊弧度來著。”
“泰朵拉是個好女孩兒，對吧？”
“聊 360° = 2π 弧度之類的……”
“泰朵拉是個好女孩兒，對吧？”
“……嗯，是啊。”我表示同意。
“θ mod 2π 也聊了？”
“誒？”
“就是重複同一件事情。”
“什麼事情？”
“紙。”米爾嘉說道。
我剛把筆記本跟自動鉛筆準備好，她就立馬寫了一個式子。
θ mod 2π
我想了想。
這個……歸根結底，a mod m 這個式子本來指的就是“a 除以 m 而得到的餘數”。也就是“以 m 為模的餘數”。例如，17 mod 3 ＝ 2。這是因為，17 除以 3 而得到的餘數是 2。一般人們會把 a mod m 中的 a 和 m 都視為整數。
不過，她寫的是 θ mod 2π。這指的是，θ 除以 2π而得到的餘數？
實數除以實數而得到的餘數……怎麼思考才好呢？
我偷偷瞟了一眼米爾嘉，她正在透過車窗望著窗外。
雖然她裝出一副若無其事的樣子，但我知道她在注意我這邊。
因為是 θ，所以是關於角度的？以 2π 為模的餘數，是什麼呢？
……
“啊，我懂了。”我說道，“假設一點在圓周上不停轉動……嗯，當只轉了 θ 弧度時，這一點的位置和轉了 θ mod 2π 弧度的點位置相同，對吧？”
轉了 θ 弧度
轉了 θ mod 2π 弧度
“沒錯。”米爾嘉看向我這邊說道，“例如，對於兩個實數 x, y，我們試著思考一下下面這種關係。
x mod 2π = y mod 2π
換言之，它們的關係就是‘以 2π 為模，x, y 同余’。寫成下面這樣更容易理解一些吧。
x ≡ y (mod 2π)
該關係滿足自反律、對稱律、傳遞律，也就是等價關係。我們用這個等價關係除以實數集 
。”
“……”
“我們看 θ 這個角的時候，實際上看到的是商集的一個元素，也就是屬於 {2π × n + θ| n 為整數 } 的無數個角的重合。”
“原來如此。原來這種地方也有等價關係和商集呀。”
米爾嘉突然站了起來。
“怎麼了？”
“到了。下車吧。”
9.3.3 燈塔
我剛在車站的月台上站定，就聞到了大海的氣息。
“這邊。”出了車站，她拐進了一條小道，頭也不回。
“等我一下啊。”
我們穿過小路，純白的燈塔映在碧藍的天空上。
“那邊。”米爾嘉說道。
我們從正面進了燈塔。螺旋樓梯坡度很陡，一直延伸到了塔頂。
米爾嘉沿著樓梯一步步向上爬，我也只好跟著她爬上去。
轉了無數圈後，我們到了塔頂。
我們打開白色的門，走到外面。寬闊的海洋頓時佔據了我們的整個視野。
可以看到那很遙遠很遙遠的遠方的海平面。
海浪一刻不間斷地發出細碎的光亮。
從燈塔上面看到的大海，竟有這麼美啊。
春天的海。
一個遊客也沒有。
只有微風輕輕吹拂而過。
海水的味道很強烈。
“有人建議我去留學。”米爾嘉說道。
“誒？”
“有人建議我去留學。”米爾嘉重複道。
“誒……”
“有人建議我高中畢業以後，去美國的大學留學。”
“……誰建議你的？”
“雙倉博士。美國數理研究所的所長，我的阿姨。”
“你已經……決定了？”
“決定了。”
“你要去，對吧？”
“對。”米爾嘉點點頭。
“……”我的胸口，漸漸冰冷。
“我要研究數學。在那邊上大學會很忙，但是應該能盡情研究數學。今年我去了很多次美國，還參觀了雙倉博士的研究所。”
這……我……我在幹什麼？
我想過高中畢業以後，跟米爾嘉去同一所大學嗎？
明明都沒跟她聊過以後的打算……
不，不對。可是，原來如此啊……
一旦畢了業，我們就該各奔東西了。
“……我都不知道。”我過了一會兒才開口道。
“嗯？”米爾嘉轉向我這邊。海風掀起她的長髮。
“這個建議，雙倉博士很久很久以前就提了，對吧？可是，直到今天為止，我一丁點兒都不知道。關於你今後的打算……”
“……”
“你不信我。”我察覺到自己這話有些欺負人。
“什麼都沒跟你說，是因為我之前還沒想好。”她說道。
我無視了她語氣中的困惑。
“那就是說，我已經……已經不能繼續待在你身邊了？”
我到底在說什麼啊？
“不是的。我只是……想告訴你。”
可是，我聽到了這些，又該說什麼才好呢？
9.3.4 海邊
我們默默地走下燈塔，沿著漫長的沙灘並肩走著。
湧來，又遠去的 —— 海浪。
來來去去，反反覆覆 —— 一浪又一浪。
海浪爬升處，留下了許許多多的海草。
米爾嘉要留學？也難怪。以她的能力，美國只是小意思，她應該在更廣闊的世界學習更豐富的知識。她有這份實力。
反過來，弱小的我又該如何？對於我來說無可替代的女生想展翅飛翔，而我只能說些風涼話……我真孩子氣。
我一直都這麼孩子氣。
這……讓我很不甘心，很丟臉。
這時，我的左臉遭受到了巨大的衝擊。
我差點跌倒。這一瞬間過後，我意識到這份衝擊是疼痛。
“笨蛋！”
米爾嘉怒氣沖沖地抬著手。
“誒？”我把歪了的眼鏡重新戴好。
“反正……你肯定又在想‘真不甘心’‘真丟臉’吧？”
米爾嘉放下手。
“你個笨蛋，‘不甘心’能改變什麼？‘真丟臉’又能改變什麼？就算你難受消沉，世界也不會因為你而有一絲改變。”
“我……”
“你腦子很聰明。看看周圍，用你那聰明的腦子好好想想。大家都喜歡你。泰朵拉、盈盈、尤里、你媽……你難受消沉了，大家都不會開心的。所以，別再消沉下去了！”
“我……”
“別消沉了，別消沉了，別迷戀消沉的自己了！”
“我……我就是個小孩，一個總在同一個地方來回轉圈的小孩。”
米爾嘉的語氣忽然輕柔了許多。
“你……能看到所有的維度麼？”
“……”
“你只能看到在圓周上轉動的點。”
“……”
“你看不到螺旋。”
“……”
“所以，別消沉了……喂，別消沉了。”
米爾嘉說著，低下了頭。
9.3.5 消毒
米爾嘉注視著腳邊的沙子，而我注視著米爾嘉。
臉上挨了米爾嘉的暴擊，現在還在一陣陣作痛。
不過，感覺堵在心裡的東西消散了。
“就算你難受消沉，世界也不會因為你而有一絲改變。”
“別迷戀消沉的自己了！”
她說的話很狠，但說得沒錯。
高中畢業以後，米爾嘉要去留學。
我必須徹底接受這個事實。
這是在當前這個時間點，我能做到的。首先，要從這一步開始。
“那個……米爾嘉。”
“……”米爾嘉抬起頭。
“很多很多事都……對不起，我這麼不振作，對不起。”
“喔……”她盯著我的臉。
“我會努力不讓自己消沉的。”
“紅了。”她指著我的左臉。
“誒？”我蹭了蹭臉，手上有淡淡的血跡。
“是我的指甲撓的吧？”米爾嘉看著自己的指尖。
“啊，剛剛……”扇我巴掌的時候刮到了麼。
“消個毒吧。”她一下子把臉靠了過來 ——
輕輕舔了一下我的臉。
天吶！
“消毒完畢 —— 有海水的味道。”
米爾嘉說著，溫柔地微微笑了。
如果你也想成為數學家，
那你就必須有這樣的覺悟：著重為了未來而工作。
——《關於數學的三次對話》[5]