關於微積分的演化歷程,我們講述到了1873年,此時離歐拉辭世將近一個世紀,而距牛頓和萊布尼茨初創微積分已逾兩個世紀。及至這時,柯西、黎曼和魏爾斯特拉斯為推進微積分嚴格化而做的工作,足以令隨後可能登場的任何後世的伯克萊們三緘其口。那麼,在分析學中還遺留著有待攻克的難題嗎?
答案當然是……「當然」。當數學家們竭盡全力建立像連續性和可積性這樣一些基本概念時,他們取得的巨大成功也引出了連帶的問題,這些問題或者具有誘惑力,或者極端困難,或者既富誘惑力又極端困難。有許許多多獨具特色的例子,從這些例子中可以窺視未來的研究途徑,而魏爾斯特拉斯的病態函數就是這些例子中最著名的一個。下面我們將要考察幾個其他的例子,這些例子將在本書其餘幾章討論。
第一個例子就是通常所說的「直尺函數」,是在約翰尼斯·卡爾·托梅(1840—1921)於1875年所寫的一本書中提出的,這是一個簡單但是帶有挑戰性的例子。他在介紹直尺函數時用這樣的開場白:「在單獨的點連續或者不連續的可積函數是五花八門的,但是最重要的是識別那些通常是無限不連續的可積函數。」1
1 Johannes Karl Thomae, Einleitung in die Theorie der bestimmten Integrale, Halle, 1875, p. 14。
托梅函數是在開區間(0, 1)上由
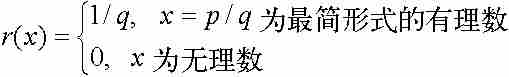
定義的函數。由此可知,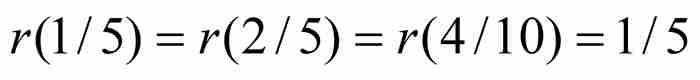 ,而
,而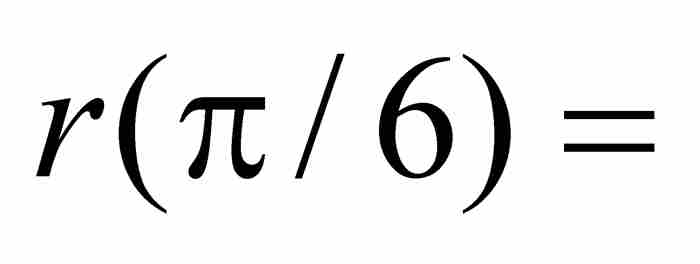
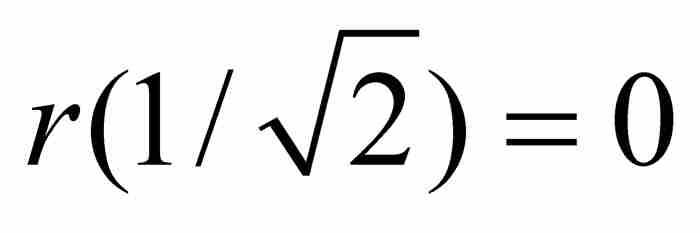 。圖10-1顯示這個函數在
。圖10-1顯示這個函數在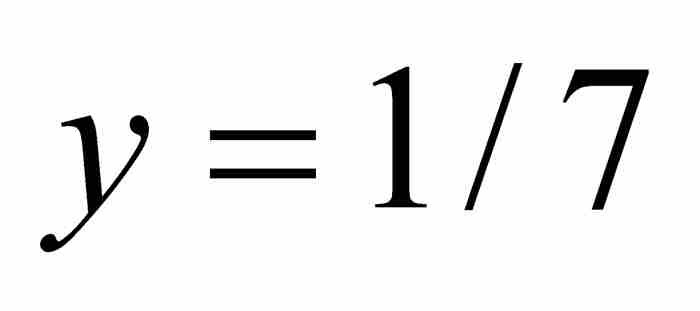 之上的部分圖形;在
之上的部分圖形;在 之下,圖中散列點的密集程度是難以想像的。這個圖形由於呈現一條直尺上的垂直刻度,因而得名。
之下,圖中散列點的密集程度是難以想像的。這個圖形由於呈現一條直尺上的垂直刻度,因而得名。
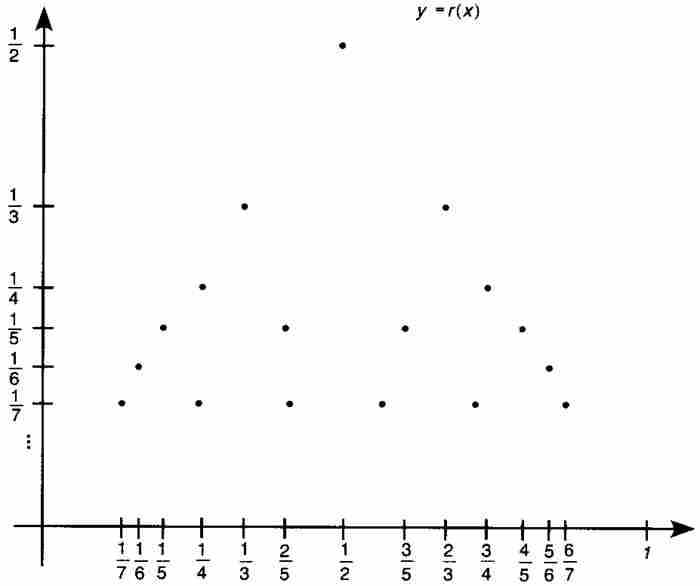
圖 10-1
應用前一章引進的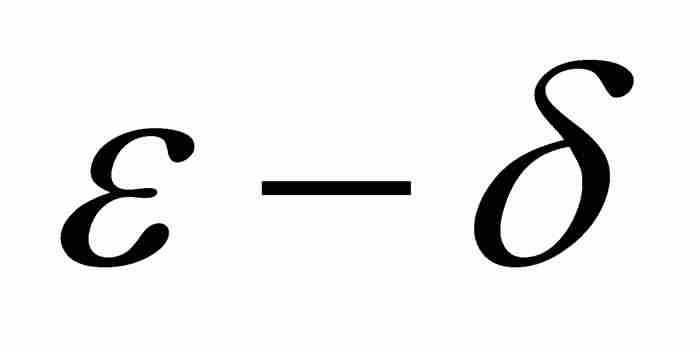 定義,很容易證明下面的引理。
定義,很容易證明下面的引理。
引理 如果a是區間(0, 1)內的任意點,那麼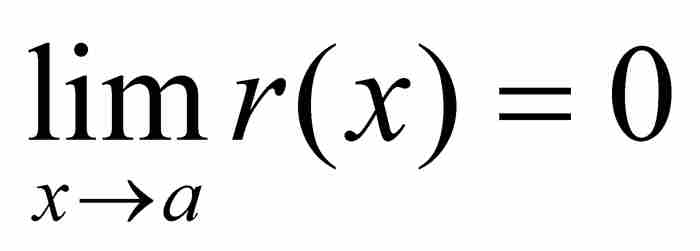 。
。
證明 對於 ,我們選擇一個滿足
,我們選擇一個滿足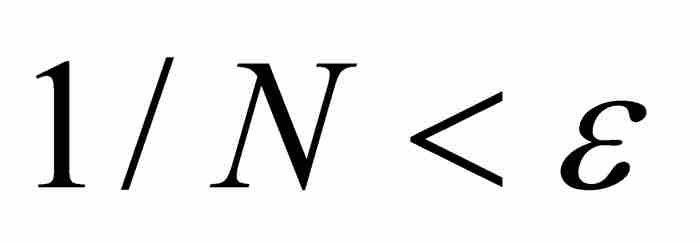 的自然數N。證明依據如下結果:在區間(0, 1)內僅有有限個最簡形式的有理數是以N或者更小的自然數作為分母的。例如,以5或者小於5的自然數作為分母的這種分數有1/2, 1/3, 2/3, 3/4, 1/5, 3/5和4/5。由於這個集合是有限的,我們可以求出一個足夠小的正數δ,使得區間(a-δ, a+δ)落入(0, 1)內,並且這個區間不包含這些分數(a除外)。現在選擇滿足0<|x-a|<δ的任意x,並且考慮兩種情形。第一,如果x=p/q是最簡形式的有理數,那麼
的自然數N。證明依據如下結果:在區間(0, 1)內僅有有限個最簡形式的有理數是以N或者更小的自然數作為分母的。例如,以5或者小於5的自然數作為分母的這種分數有1/2, 1/3, 2/3, 3/4, 1/5, 3/5和4/5。由於這個集合是有限的,我們可以求出一個足夠小的正數δ,使得區間(a-δ, a+δ)落入(0, 1)內,並且這個區間不包含這些分數(a除外)。現在選擇滿足0<|x-a|<δ的任意x,並且考慮兩種情形。第一,如果x=p/q是最簡形式的有理數,那麼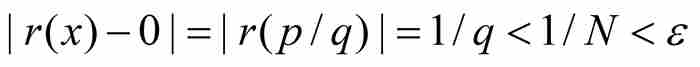 ,因為只要
,因為只要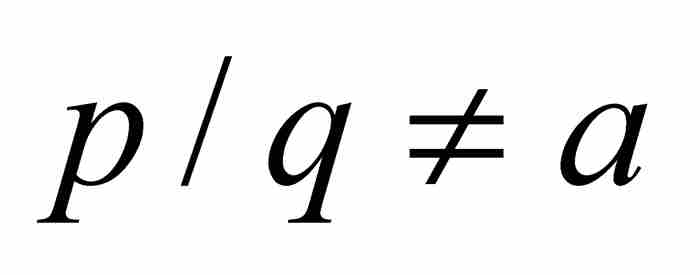 在區間(a-δ, a+δ)內,q必定大於N。第二,如果x為無理數,那麼同樣有
在區間(a-δ, a+δ)內,q必定大於N。第二,如果x為無理數,那麼同樣有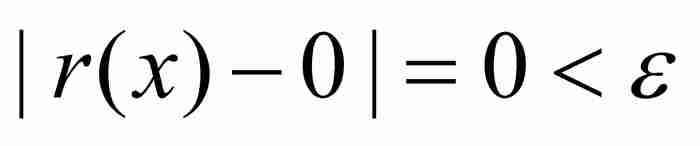 。無論哪一種情形,對於
。無論哪一種情形,對於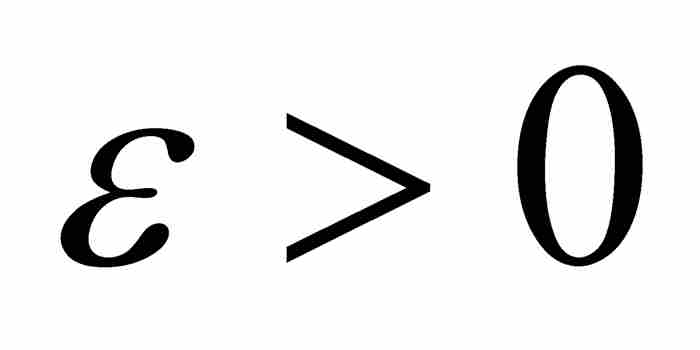 ,我們已經求出一個
,我們已經求出一個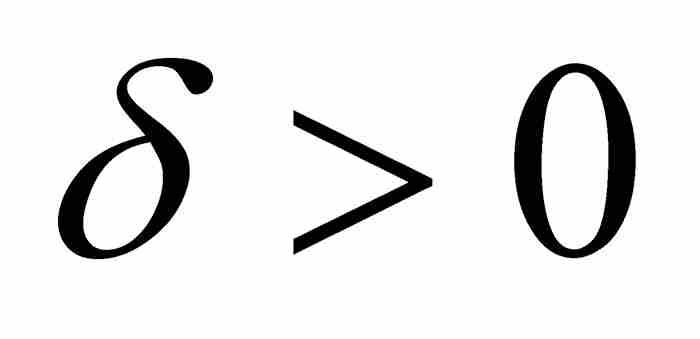 ,只要
,只要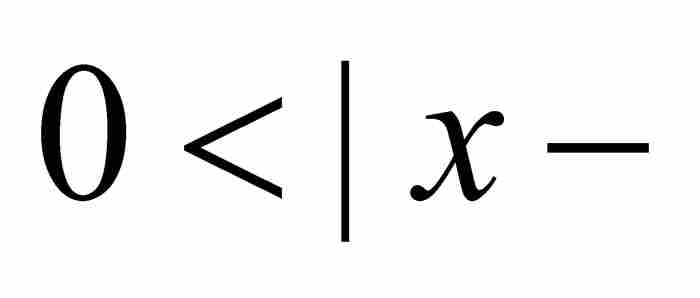
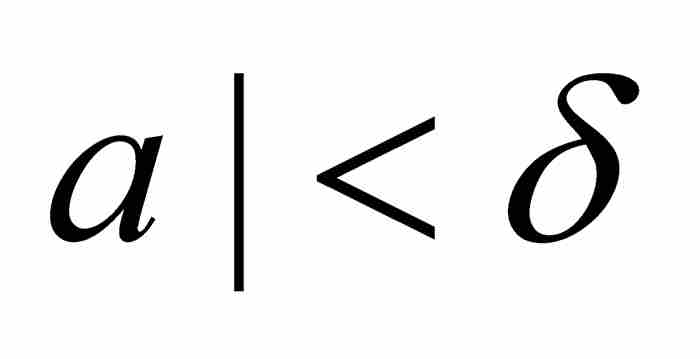 ,就有
,就有 。根據函數的極限的定義,
。根據函數的極限的定義,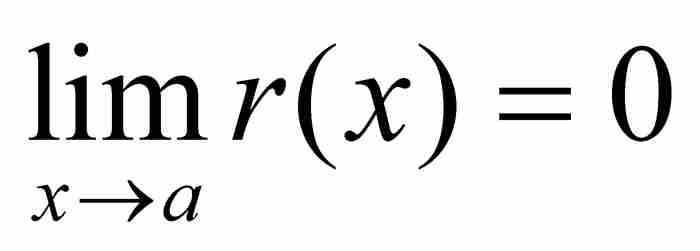 。
。
以這個引理作後盾,我們可以證明直尺函數具有極為驚人的性質:它在區間(0, 1)的每個無理數點是連續的,而在其中每個有理數點是不連續的。這是立即可得的結果,因為如果a為無理數,那麼根據引理,有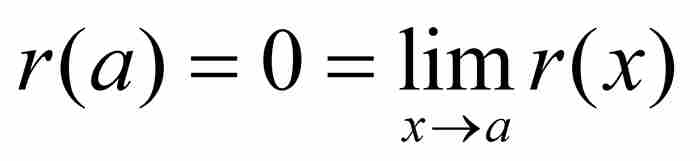 ——恰好符合r(x)在x=a連續的柯西定義。另一方面,如果a=p/q是一個最簡形式的有理數,那麼
——恰好符合r(x)在x=a連續的柯西定義。另一方面,如果a=p/q是一個最簡形式的有理數,那麼
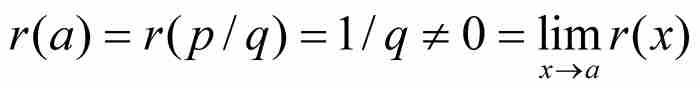
所以直尺函數在x=a是不連續的。
這個結果向我們展現一種奇特的情景:直尺函數在無理數點是連續的(我們越來越不可靠的直覺把它視為「不間斷的」),而在有理數點是不連續的(「間斷的」)。絕大部分人會發覺,函數的連續點同不連續點能夠如此纏結在一起是難以想像的。但是,上面的數學論證是明確無誤的而不是模稜兩可的。
我們把直尺函數的定義域從區間(0, 1)擴展到全部實數集,這將會是有用的。為此目的,令新函數在每個整數點取值1,並且把r(x)的拷貝置於每個子區間(1, 2), (2, 3), …之上。更確切地說,我們定義擴展的直尺函數R為
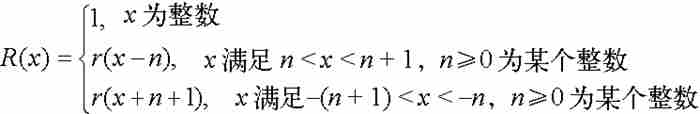
按照上面的定義,對於任何實數a,我們有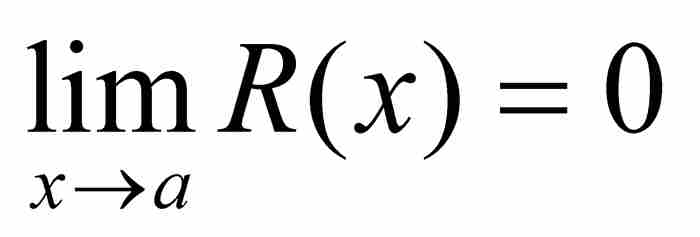 ,所以R在每個無理數點是連續的,而在每個有理數點是不連續的。
,所以R在每個無理數點是連續的,而在每個有理數點是不連續的。
直尺函數提出一個自然的問題:「怎樣反轉角色方能創建一個在每個有理數點連續而在每個無理數點不連續的函數?」這個問題雖然說起來非常簡單,但是它的解答是很深奧的,而且是極為有趣和令人著迷的。這將是下一章討論的主題。
直尺函數R值得注意的另一個原因,在於它不連續的範圍儘管是無限的,然而它在區間[0, 1]是可積的。自然,這就是托梅在上面那本書的開場白中道出的實質。為了證明這一點,我們利用第7章中的黎曼可積性條件。
我們從一個d > 0的值和一個固定的函數振幅 σ> 0開始。然後選擇一個滿足1/N < σ 的自然數N。按照前面的論證,我們知道區間[0, 1]僅含有有限個最簡形式的有理數p/q,使得R(p/q)≤1/N,也就是說,這些最簡形式的有理數的分母不大於N。我們令M為這種最簡形式的有理數的個數,並且劃分區間 [0, 1]使其中每個最簡形式的有理數落入寬度為d/2 M的一個子區間內。我們把這些子區間稱為A類子區間,也就是函數振幅超過σ的子區間。用黎曼的術語,我們有
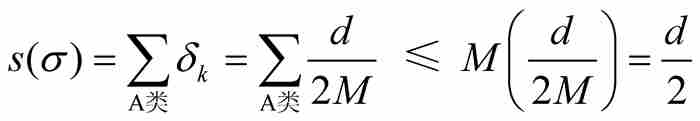
所以當 時
時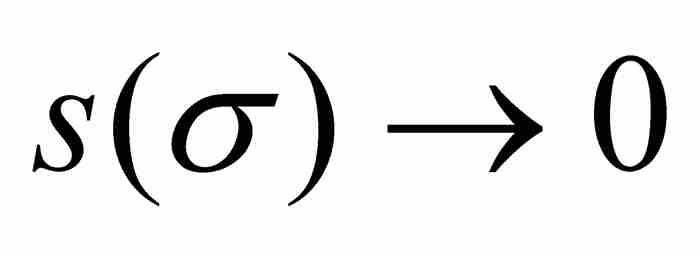 。這正好是黎曼需要建立的可積性條件。換句話說,積分
。這正好是黎曼需要建立的可積性條件。換句話說,積分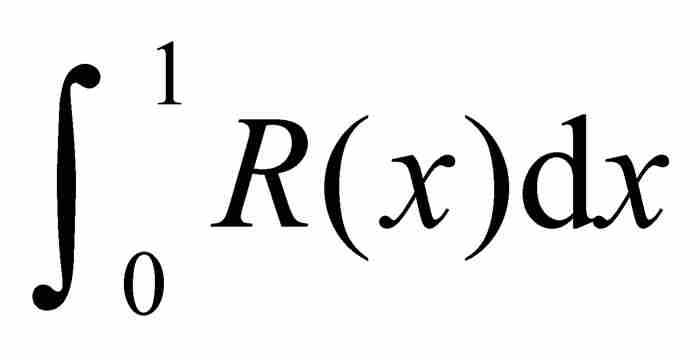 存在。當知道這個積分存在後,我們很容易進一步證明
存在。當知道這個積分存在後,我們很容易進一步證明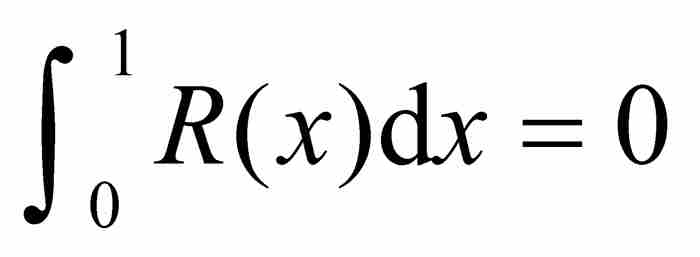 。
。
應當說明,直尺函數所扮演的角色同第7章中的黎曼病態函數是相仿的。這兩種函數都是無限不連續的,然而又都是可積的。它們之間的主要差異在於直尺函數更為簡單,而在某些情況下,小小的簡單性卻是不可輕視的。
這些例子提出一個令數學家們神往的問題。回憶一下,狄利克雷函數是處處不連續的和非黎曼可積的。相反,直尺函數僅在有理數點是不連續的,並且是可積的。毫無疑問,直尺函數存在一種極端的不連續性,然而它仍然具備足夠的連續性使其成為可積的。憑借這樣的證據,數學家們猜測,一個黎曼可積函數雖說可能是不連續的,但是不至於過分地不連續。函數的連續性與可積性問題將使分析學家們在19世紀剩餘的歲月忙得不亦樂乎。從本書最後一章我們會看到,這個舉世矚目的問題是由亨利·勒貝格著手研究並於1904年最終解決的。
我們在下面舉出的三個例子是相互關聯的,所以可以把它們放在一起考察。像直尺函數一樣,這幾個函數具有令人驚奇的特性,所以是大多數分析學教科書務必討論的。
首先,我們定義函數
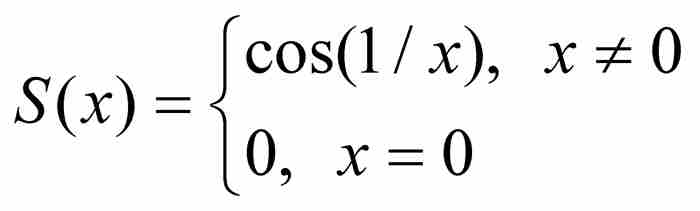
並且在圖10-2中畫出它的圖形。當x趨近零時,其倒數1/x無限增加,致使cos(1/x)在原點的任何鄰域內從-1到1無限次地來回擺動。如果用一種委婉的說法,那就是函數S(x)在原點附近劇烈地振蕩。
通過引進序列 ,並且考察函數圖形上對應於
,並且考察函數圖形上對應於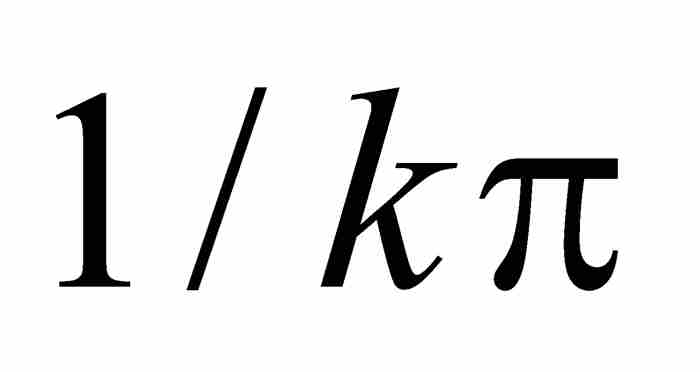 的點,我們證明不存在極限
的點,我們證明不存在極限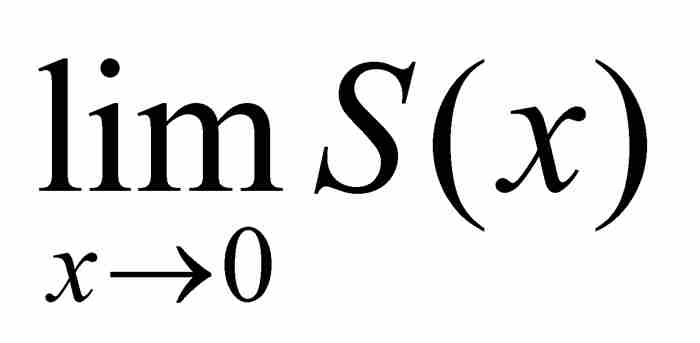 。如圖10-2中所示,我們的函數交替地選取峰值與谷值。就是說,我們有
。如圖10-2中所示,我們的函數交替地選取峰值與谷值。就是說,我們有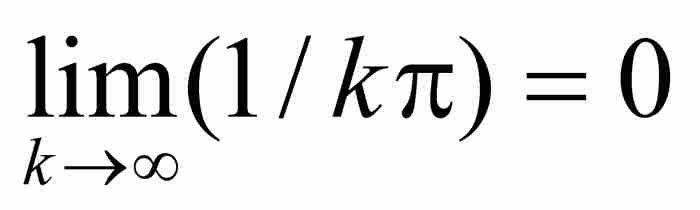 ,但是
,但是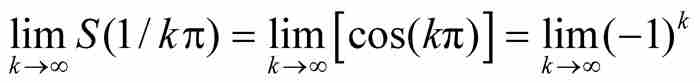 。由於後面這個極限不存在,極限
。由於後面這個極限不存在,極限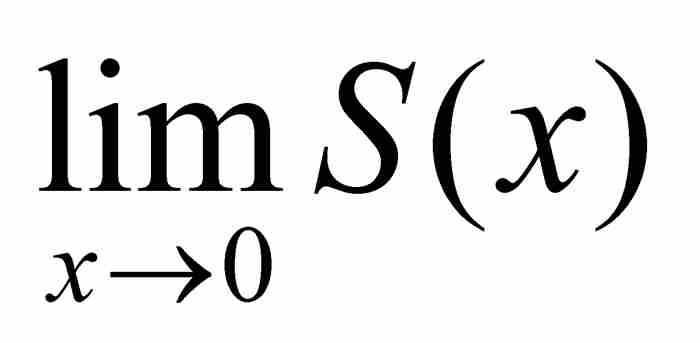 也就不存在,而這本身又意味著
也就不存在,而這本身又意味著 在
在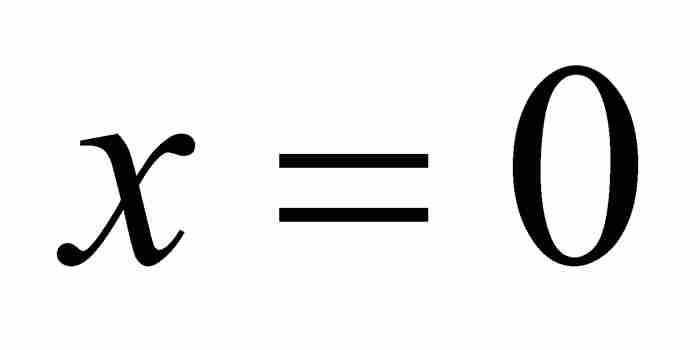 是不連續的。
是不連續的。
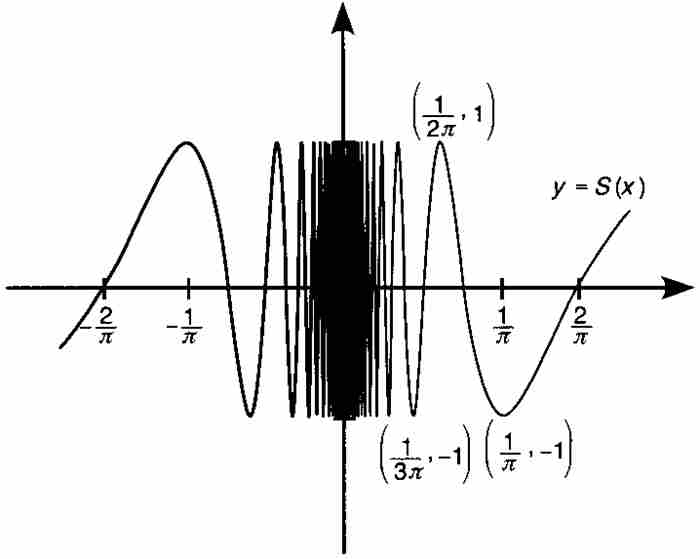
圖 10-2
與此相關的第二個函數是
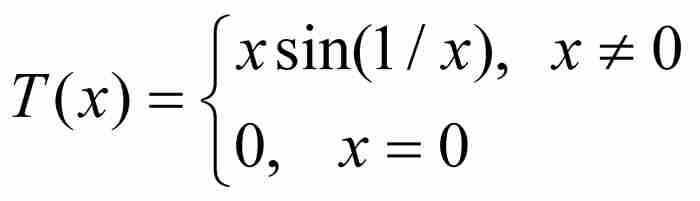
它的圖形在圖10-3中給出。由於函數定義中包含乘數x,當x趨近原點時T的無限次振蕩逐漸衰減。
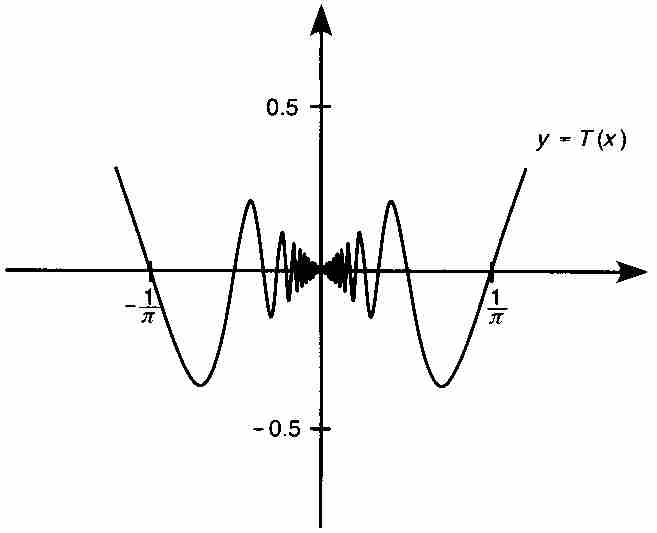
圖 10-3
在任何非零點,T是兩個連續函數 和
和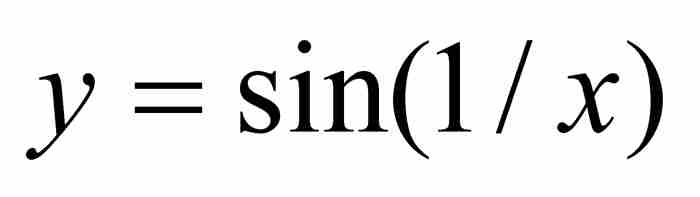 的乘積,所以它本身是連續的。由於
的乘積,所以它本身是連續的。由於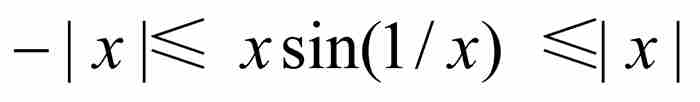 和
和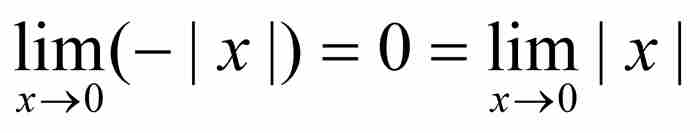 ,擠壓定理保證
,擠壓定理保證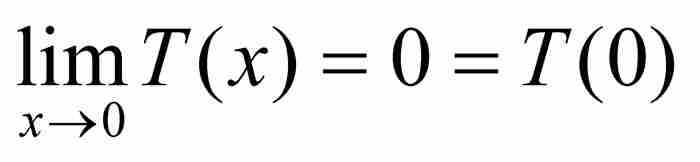 ,所以T在
,所以T在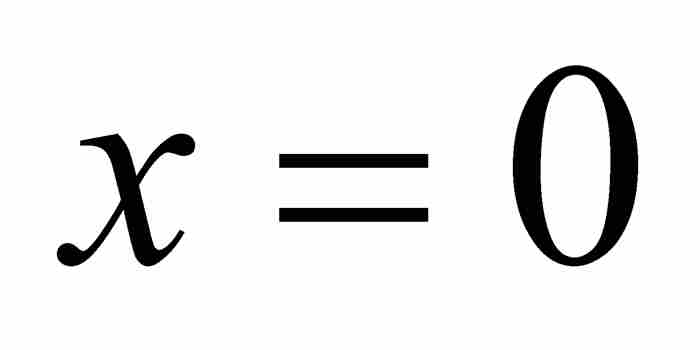 也是連續的。總之,T是一個處處連續的函數。它經常被作為一個例子引用,用來說明函數是「連續的」與「一筆就可以畫出圖形」不是同一回事。在初級微積分教程中,後面這種表述可能算是一種有用的特徵,但是在原點的鄰域內,不可能用所有這樣上下振蕩的值繪製
也是連續的。總之,T是一個處處連續的函數。它經常被作為一個例子引用,用來說明函數是「連續的」與「一筆就可以畫出圖形」不是同一回事。在初級微積分教程中,後面這種表述可能算是一種有用的特徵,但是在原點的鄰域內,不可能用所有這樣上下振蕩的值繪製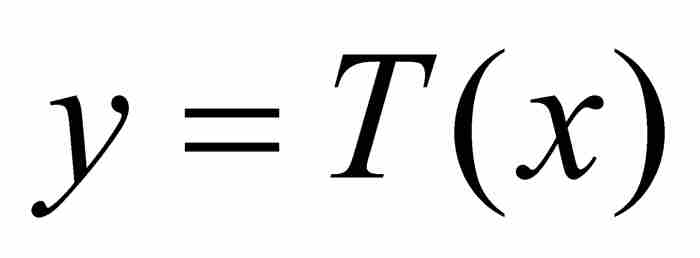 的圖形。
的圖形。
最後,我們來考察第三個函數,這是三個相關函數中最富刺激性的函數,其定義為
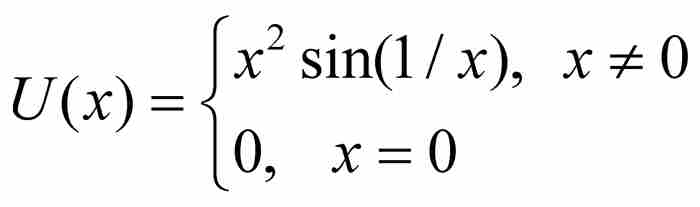
表達式中的二次係數x2加速函數曲線在原點附近的衰減。由於U(x) = xT(x),而其中兩個因式是處處連續的,所以U是處處連續的函數。
這時困難在於可微性。在任何點 ,U無疑是可微的,並且由微分法則有
,U無疑是可微的,並且由微分法則有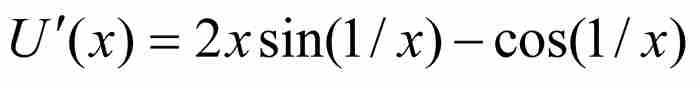 。函數在
。函數在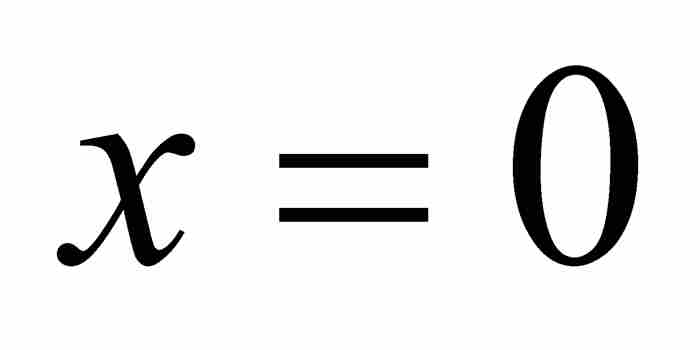 也是可微的,這是因為
也是可微的,這是因為
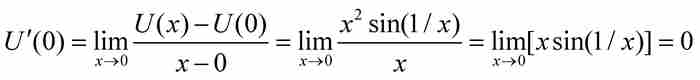
其中最後一個極限利用了我們剛見到的同樣的「擠壓」。所以,儘管函數U的值在原點附近無限次地上下擺動,它在那裡依然具有一條水平切線。
我們證明了U是處處可微的,它的導數為
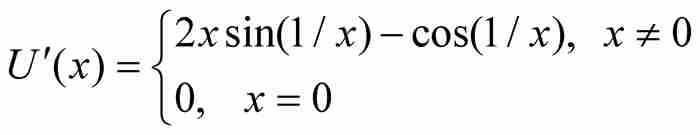
可惜這個導數不是連續函數,我們只要再次考慮序列{1/kπ},並且注意極限
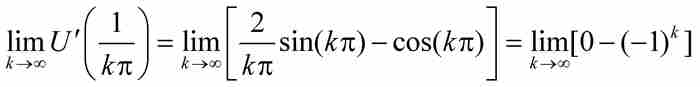
並不存在,就知道這一點。因此,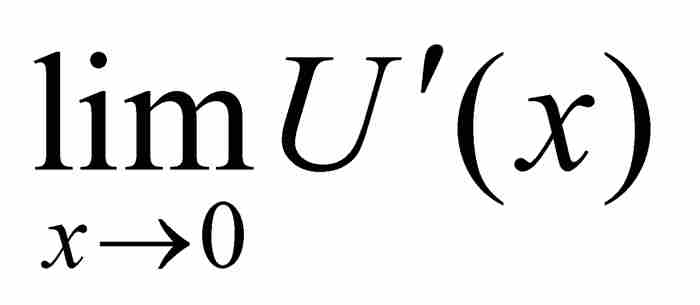 是不存在的,所以
是不存在的,所以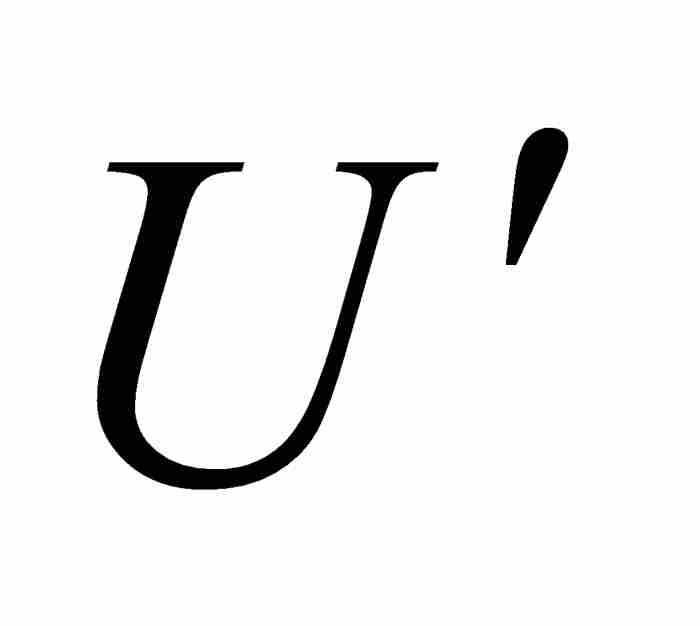 在
在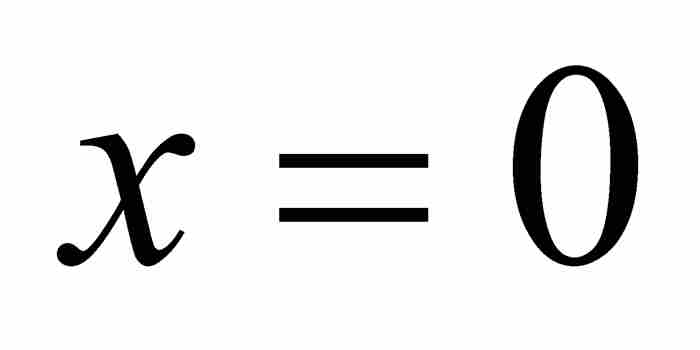 是不連續的。總之,U是一個具有不連續導數的可微函數。
是不連續的。總之,U是一個具有不連續導數的可微函數。
這個例子不禁使我們想起那個著名的定理:一個可微函數是連續函數。對於這個定理作出如下修正是自然的:「一個可微函數的導數必定是連續函數。」然而,函數U(x)這個例子表明,這個修正是錯誤的。
這三個函數同樣使連續性同介值定理之間的關係出現混亂。正如我們所見,柯西曾經證明,一個連續函數必定遍取介於它的任何兩個值之間的所有值。可以把這個幾何上不言而喻的事實看作連續性的本質,而人們據此可以推測,一個函數是連續的,當且僅當它在定義域的每個區間上具備介值特性。
但是,這個猜想再次被證明是錯誤的。讓我們考慮上面第一個例子的函數S(x),把它作為一個反面例子。我們已經看出S在原點是不連續的,但是可以斷定它在每個區間上具備介值特性。
為了證明這種特性,假定對於a < b有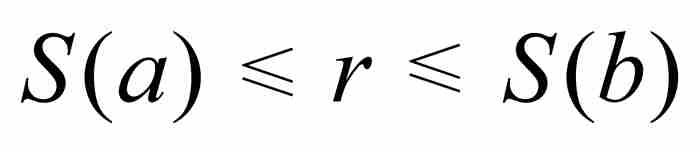 。根據餘弦函數的性質,我們知道
。根據餘弦函數的性質,我們知道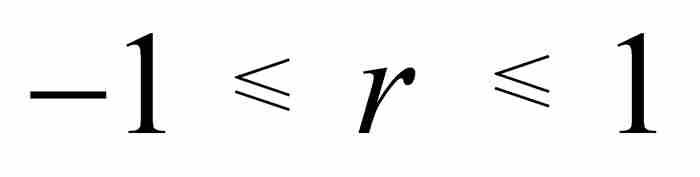 。現在考察下面兩種情況。
。現在考察下面兩種情況。
首先,如果0 < a < b,或者a< b < 0,那麼S在整個區間[a, b]上是連續的,所以根據介值定理,對於(a, b)中的某個c有S(c) = r。
其次,如果a< 0 < b,我們可以固定一個滿足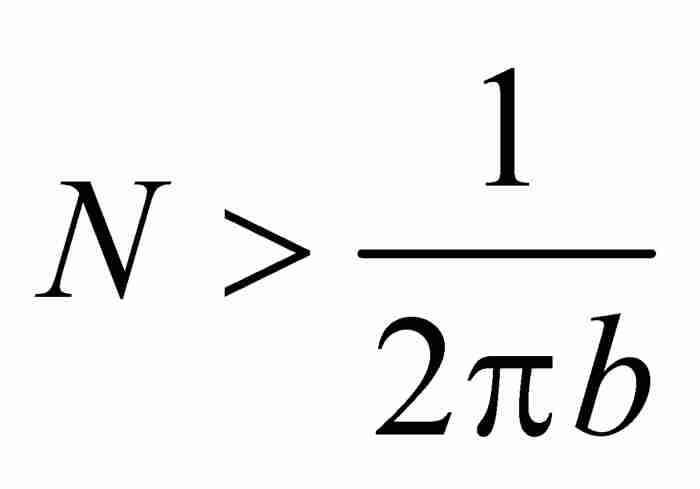 的自然數N。於是,有
的自然數N。於是,有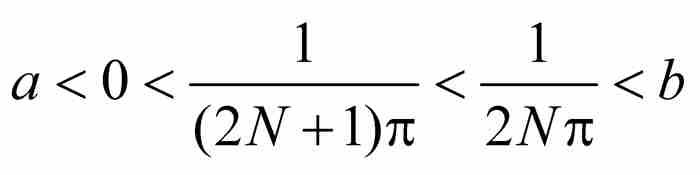 ,並且當x在正數
,並且當x在正數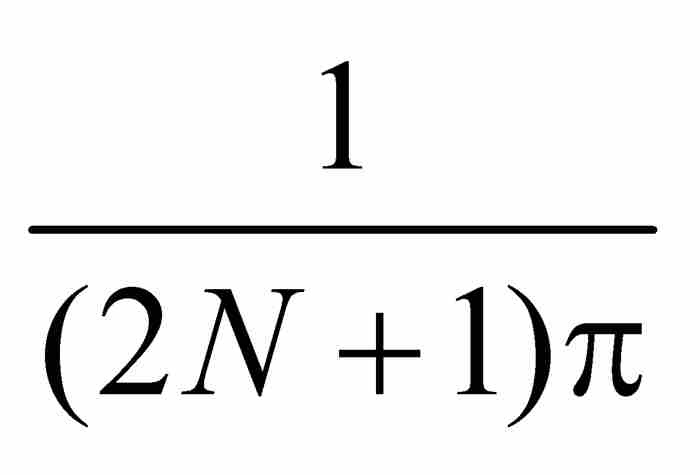 與
與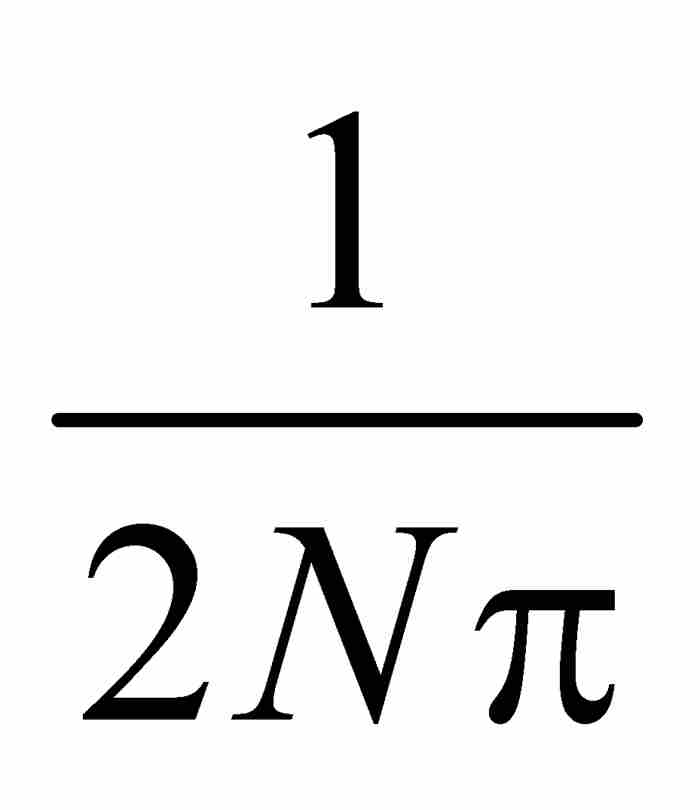 之間取值時,1/x在2 Nπ與
之間取值時,1/x在2 Nπ與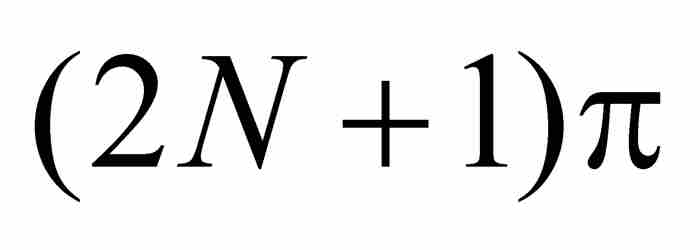 之間取值。在這個過程中,
之間取值。在這個過程中,
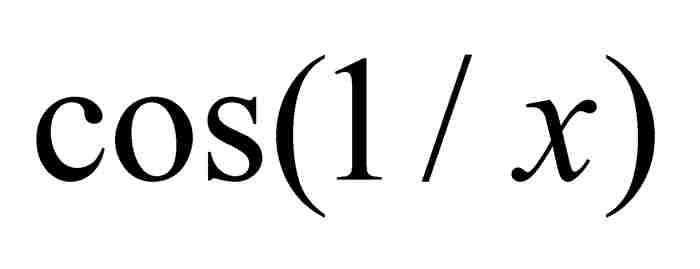 的值從
的值從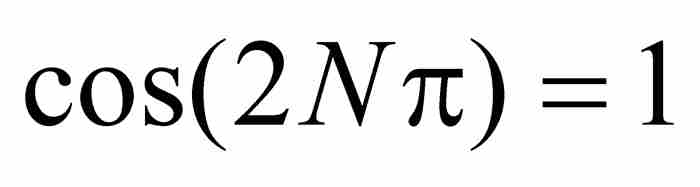 連續地變化到
連續地變化到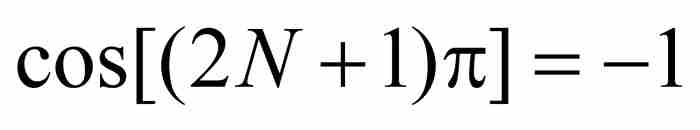 。根據介值定理,在
。根據介值定理,在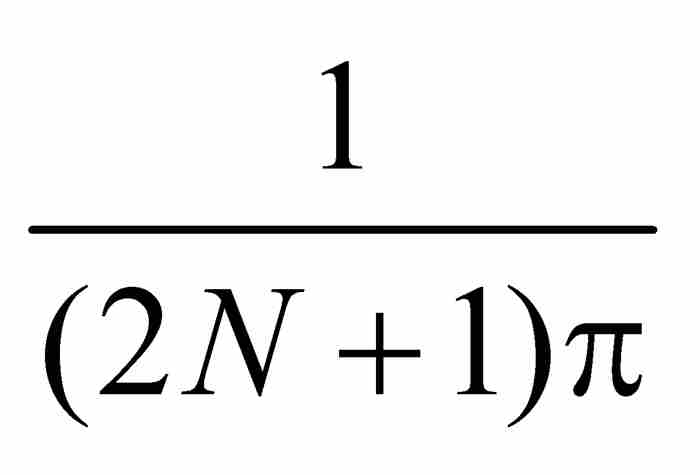 與
與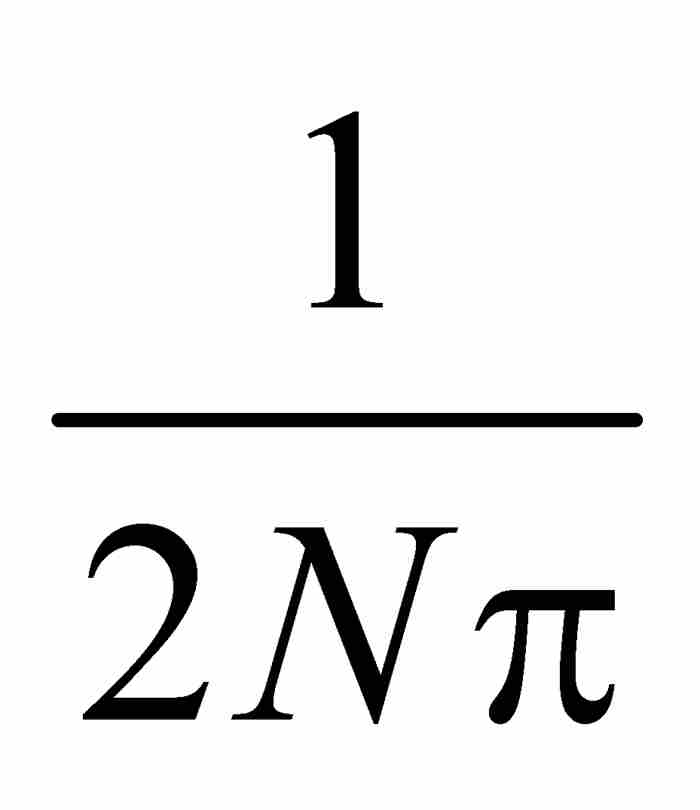 之間(並因此而在a與b之間)必定存在一個滿足
之間(並因此而在a與b之間)必定存在一個滿足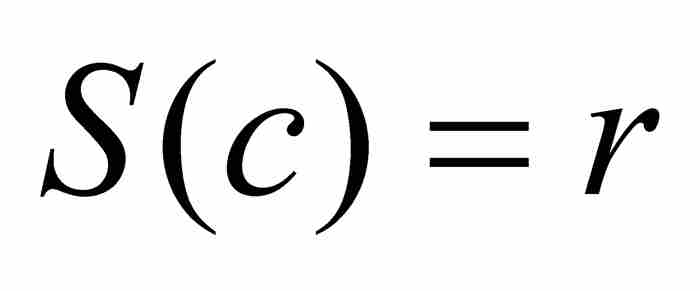 的c。上述斷言由此得以證明。
的c。上述斷言由此得以證明。
總而言之,我們列舉的三個例子證明了一個可微函數的導數並非一定是連續的,同時,具備介值特性的函數未必一定是連續函數。這兩個結論似乎顯得離奇,然而還有一個更令人吃驚的結果。
這個結果是由法國數學家伽斯騰·達布(1842—1917)發現的。達布以對分析學的兩大貢獻而聞名於世。第一,他簡化了黎曼積分的推演,以簡便得多的方法達到同樣目的。當今的分析學教科書在導入積分時,傾向於採用達布精緻的處理步驟而不用黎曼原來的方法。
不過我們在這裡要提出的是達布的第二個貢獻。那就是現在所說的「達布定理」,他在這個定理中證明了函數的導數雖然不一定是連續的,但是必定具備介值特性。達布的論證依據是任何一本分析學入門教材都要介紹的兩個結果:其中一個是,連續函數在有界閉區間上取一個極小值;另一個是,如果g是可微函數,並且在區間(a, b)內的點x = c具有一個極小值,那麼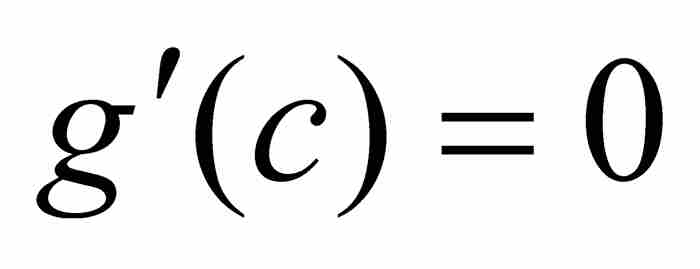 。
。
達布定理 如果f (x)是區間[a, b]上的可微函數,而r是任意一個滿足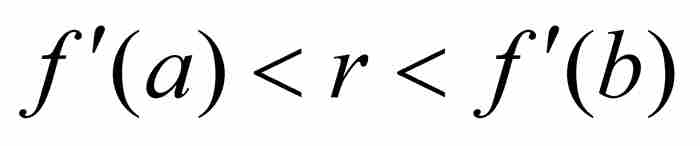 的數,那麼在(a, b)內存在一點c滿足
的數,那麼在(a, b)內存在一點c滿足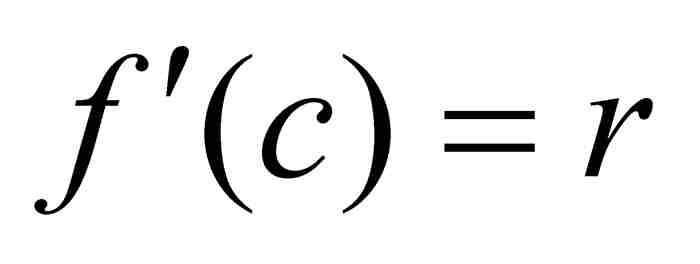 。
。
證明 我們從引進一個新函數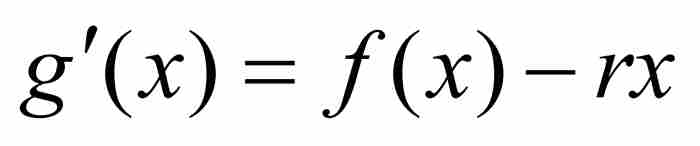 入手。由於f是可微的,它是一個連續函數,而rx也是連續的,所以g在[a, b]上是連續的。進一步說,g是可微的,因為
入手。由於f是可微的,它是一個連續函數,而rx也是連續的,所以g在[a, b]上是連續的。進一步說,g是可微的,因為 。
。
在[a, b]內存在一點c, 函數g在這個點取一個極小值。由於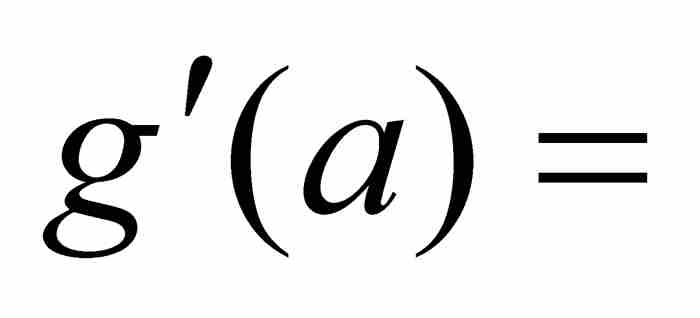
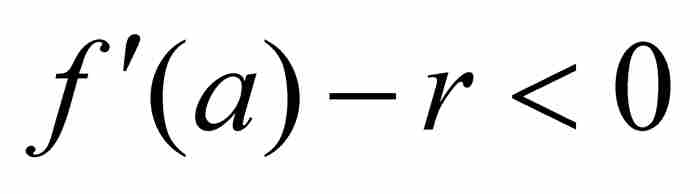 ,而
,而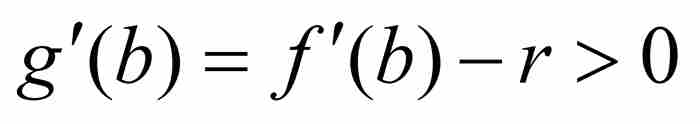 ,我們看出極小值不可能出現在端點a和b,所以c位於(a, b)內。於是,根據上面引述的第二個結果,
,我們看出極小值不可能出現在端點a和b,所以c位於(a, b)內。於是,根據上面引述的第二個結果,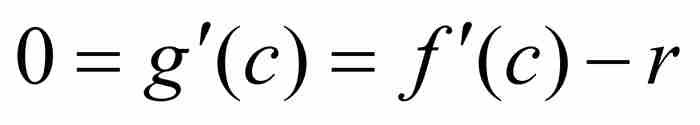 ,或者簡單說
,或者簡單說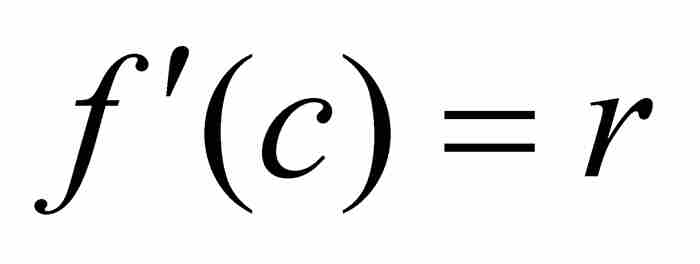
因此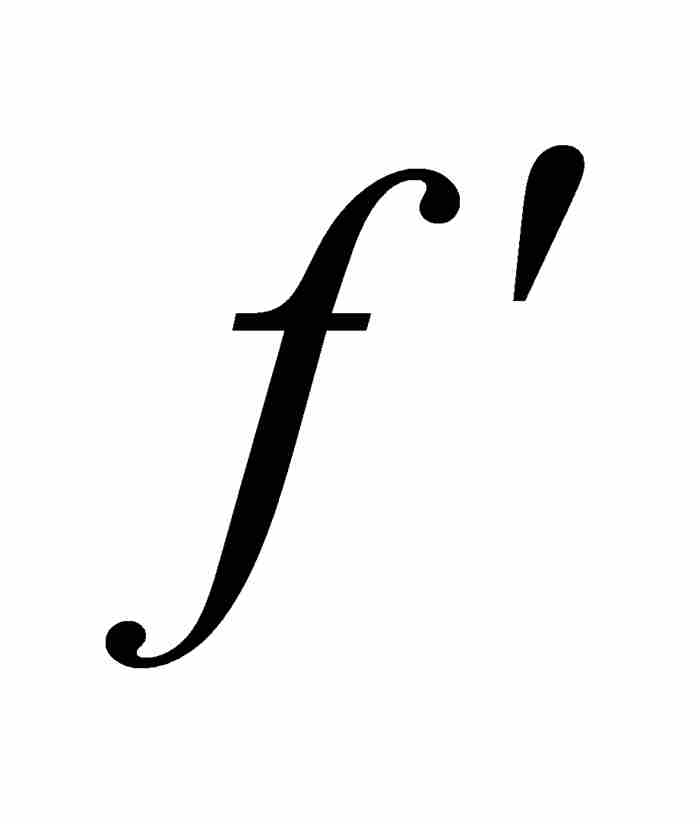 取介於
取介於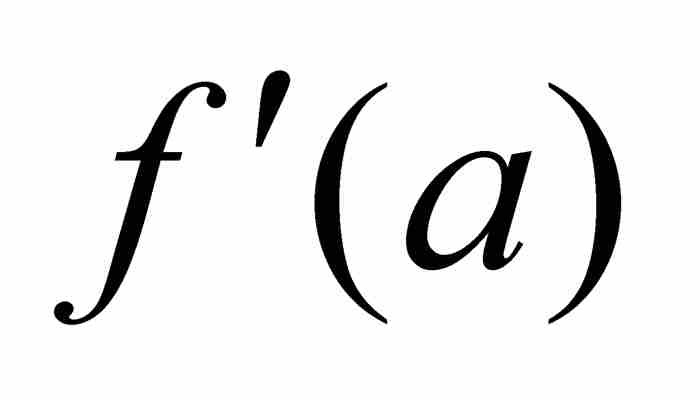 和
和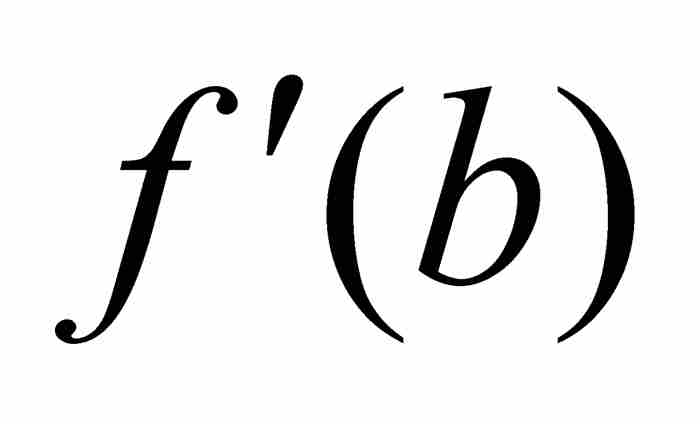 之間的這個中間值r,正如定理的要求。
之間的這個中間值r,正如定理的要求。
讀者不妨回憶一下柯西對中值定理所作的證明,為了推斷函數取中間值,他假定函數的導數是連續的。如今我們看出,柯西可以拋開他的假設而不必捨棄其結論。從達布定理還可以推出,一個不具備介值特性的函數,例如狄利克雷函數,不可能成為某個函數的導數。
達布證明了導數與連續函數同樣具有介值的特性。這又提出另外一個問題:「一個導數到底在何等程度上是不連續的?」我們在本書第13章將會看到,對於這個問題,勒內·貝爾在1899年提供了一個答案。
如果說導數遇到麻煩,那麼積分會遇到更大的麻煩。以往我們指出過,即使函數序列{fk}是點態收斂的,對於取極限和求積分的過程,一般不能推斷
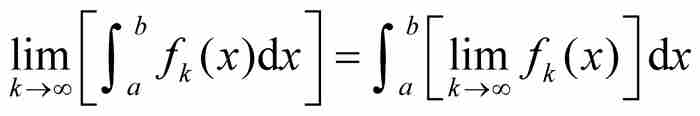 (1)
(1)
魏爾斯特拉斯證明了一致收斂是保證交換極限與積分的充分條件,但是不能反過來成為必要條件。這就是說,已經發現若干函數序列{fk}的例子,它們是點態收斂而非一致收斂的,但是式(1)對它們依然成立。數學家們或許忽略了某個中間條件,這種條件不具有一致收斂那樣強的限制,卻使我們能夠進行所渴求的對取極限與求積分的交換。
或者——乍看起來這是極端不可能的「或者」,黎曼積分的定義也許存在缺陷。按照黎曼的做法,他在處理積分中可能誤入歧途,走上一條需要某些特殊條件才能使式(1)成立的道路。倘若果真如此,那麼可以把他的積分視為不完善的。
從表面上判斷,這無異於異端邪說,因為黎曼積分已經成為數學分析的支柱。達布把它描述為「唯有最聰慧的人才能取得的」一個創舉。2 保羅·杜布瓦·雷蒙則這樣表達他的信念,黎曼的定義是無法再改進的,因為它把可積性的概念延伸到最大限度。3 不過,正如我們將會見到的那樣,種種美中不足促使大家研究定義範圍更廣闊的積分。這一研究的結果就是20世紀初建立的勒貝格積分論。
2 E. Hairer and G. Wanner, Analysis by Its History, Springer-Verlag, 1996, p. 219。
3 Thomas Hawkins, Lebesque』s Theory of Integration, Chelsea, 1975, p. 34。
概括起來說,上述幾個函數提出了這樣一些問題:
我們能構造出一個在每個有理數點連續而在每個無理數點不連續的函數嗎?
一個黎曼可積函數的不連續性可能達到何種地步?
一個導數可以在何等程度上是不連續的?
我們能以任何一種方式彌補黎曼積分的缺陷嗎?
雖然這裡並沒有列舉所有的問題,但是已經舉出的這些問題是數學分析在19世紀的最後四分之一世紀所面對的關鍵性問題。由於這些問題的特殊本質,在柯西、黎曼和魏爾斯特拉斯對分析學作出貢獻之前是很難被提出來的,就更不用說給予回答了。隨著問題變得越來越複雜,求解也就需要越來越周密的推理。在本書餘下的幾章中,我們將簡要地闡述如何尋找這四個問題的答案。
不過,我們的第一站將停留在格奧爾格·康托爾於1874年所寫的一篇論文上,正是這位天才促成了集合論的誕生,並且運用他的思想重新證明了超越數的存在。他的成就同時說明這樣一個道理,對於人們長期以來認為已經解決的問題再展開思考,還是會大有裨益的。
