約瑟夫·劉維爾（1809—1882）
普遍性成為現代分析學的核心，這是在柯西極限定理或黎曼積分中已經明顯呈現的一種潮流。這兩位超越他們前輩的數學家定義了包容一切的關鍵性概念，並且在此基礎上引出普遍性結論，這些結論不僅對於一兩個孤立事例成立，而且對於數量龐大的事例群體也是正確的。這是分析學中一項最有意義的進展。
此外，人們在17世紀還目睹了看起來彷彿相反的一種現象，那就是明顯的例子和特殊的反例在分析學中的重要性日益增加。同前面幾章討論的普遍性定理一樣，這種趨勢同樣值得我們注意。在這一章，我們首先考察約瑟夫·劉維爾於1851年發現的第一個超越數；在下一章再探討卡爾·魏爾斯特拉斯在1872年提出的令人驚訝的病態函數。這兩個結果分別是它們所處時代的巨大成就，並且提醒我們，在分析學的結論中，只要沒有由獨特的例子提供的說明，那麼就是不完全的。
為了研究超越數，我們需要對這一問題的背景有所瞭解，考察一下它是從哪裡提出來的，在以往的數十年中是如何得到提煉的，以及它的解決為什麼成為一項如此重大的成就。按照微積分自身的演進過程，我們從17世紀開始。
代數數與超越數
似乎萊布尼茨是首次提出超越量概念的人，因為他在一個數學分類方案中使用了「超越的」這個術語。在論及他新發明的微分法時，萊布尼茨指出它的應用範圍包括分式、根式以及類似的代數量，但是接著就補充道：「顯然，我們的方法也適用於超越曲線，這種曲線不能通過代數運算加以簡化，或者沒有特定的次數，因此，這種方法是一種行之有效的最普遍的方法。」 1 從這裡看出，萊布尼茨想要把那些屬於代數範疇的對象，因而是相當簡單明瞭的實體，同那些在本質上更為複雜的對象區分開來。
1 Dirk Struik, 「The origin of l'Hospital's rule」, Mathematics Teacher, vol. 56 (1963), p. 276。
這種區分在18世紀由歐拉進一步完善。歐拉在其著名的《無窮小分析引論》一書中，把「加法、減法、乘法、除法、自乘和求根」以及「方程求解」列為所謂的代數運算，而把其他任何運算歸入超越運算，如像那些涉及「指數和對數的運算，以及積分學中提供的其他大量運算」。2 他甚至走得更遠，直到提出超越量，並且舉出「不是基數乘方的數的對數」作為超越量的一個例子，不過他沒有提供嚴謹的定義，也沒有給出嚴格的證明。3
2 Leonhard Euler, Introduction to Analysis of the Infinite, Book I, p. 4。
3 Leonhard Euler, Introduction to Analysis of the Infinite, Book I, p. 80。
我們的數學先哲們往往具有正確的思想，即使他們未能把那種思想準確地表達出來。對於他們而言，某些數學對象，例如曲線、函數或者數字，明顯是可以通過基本代數運算得到的，而其他的對象則是異常複雜的，以至全然超越了代數運算，並因此而獲得「超越」這個名稱。
到18世紀後期，在勒讓德這樣一些數學家的著作中，出現了一種無歧義的定義。一個實數如果是某個具有整係數的多項式方程的解，就把它稱為代數數。這就是說，對於一個數x0，如果存在一個多項式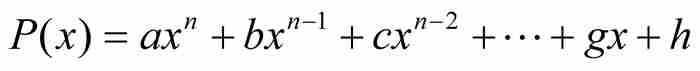
，其中a, b, c, …, g和h為整數，滿足
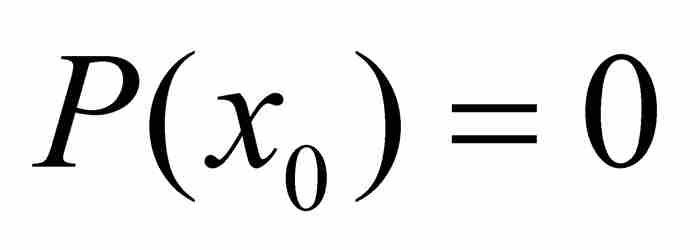，那麼x0是一個代數數。例如，
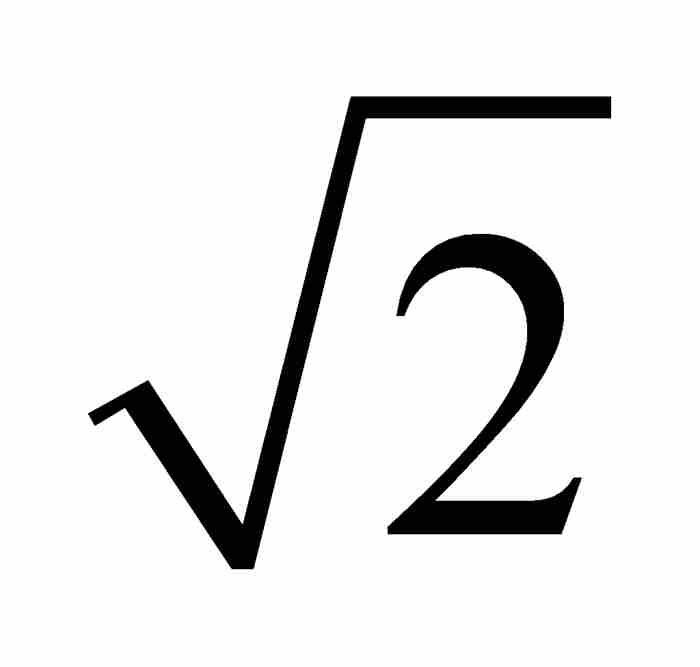是代數數，因為它是整係數二次方程
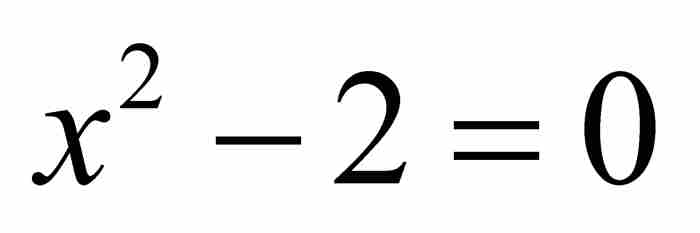的一個解。
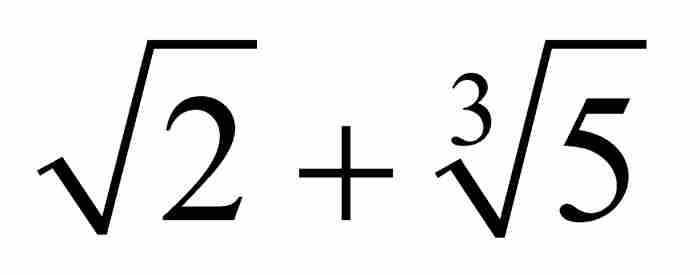也是代數數，不過，這看起來不是那麼明顯，因為它是整係數6次方程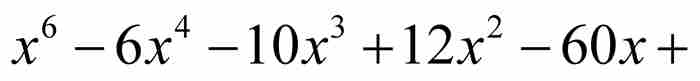
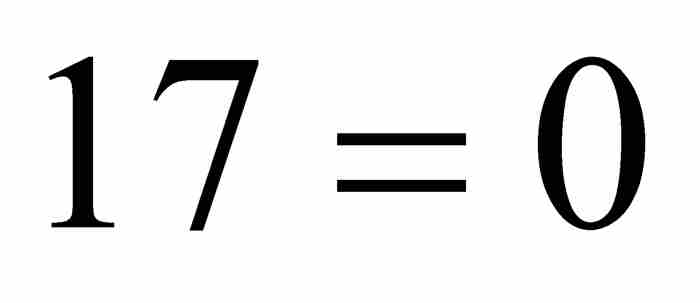的一個解。
從幾何學觀點看，一個代數數乃是函數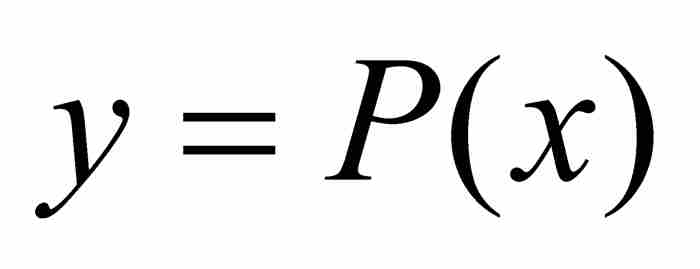
的圖形的x截距，其中P是一個具有整係數的多項式（參見圖8-1）。如果設想在同樣的坐標系中畫出係數為整數的所有線性式、二次式和三次式以及一般情況下的所有多項式的圖形，那麼它們的x截距的無窮集合都是代數數。
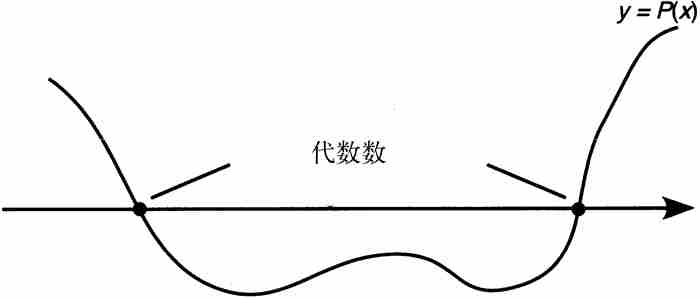
圖 8-1
這就提出一個顯而易見的問題：還存在任何其他代數數嗎？為了考慮這種可能性，我們姑且說，一個實數只要不是代數數，那麼它就是超越數。單純從邏輯上說，任何實數必定屬於這兩類數中的一類。
然而，果真存在超越數嗎？畢竟，定義一個術語並不能就保證它的實體的存在。正如一位哺乳動物學家，完全可以把一頭棲息於水中的海豚定義為「代數海豚」，而把不在水中生活的海豚定義為「超越海豚」。這裡，超越海豚這個名稱在概念上是無歧義的，但是並不存在這樣一個物種。
數學家們必須面對同樣的可能性。那麼，超越數是否只是全憑想像而精心定義的一種虛構的數呢？要是這樣，所有代數數的x截距能夠完全佈滿x軸這條直線嗎？如果不能，我們又從哪裡去尋找一個不等於任何整係數多項式方程的x截距的數呢？
作為走向答案的第一步，我們注意到，一個超越數必定是無理數。這是因為，如果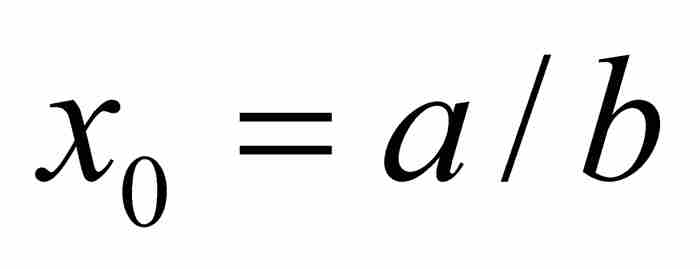
是有理數，那麼
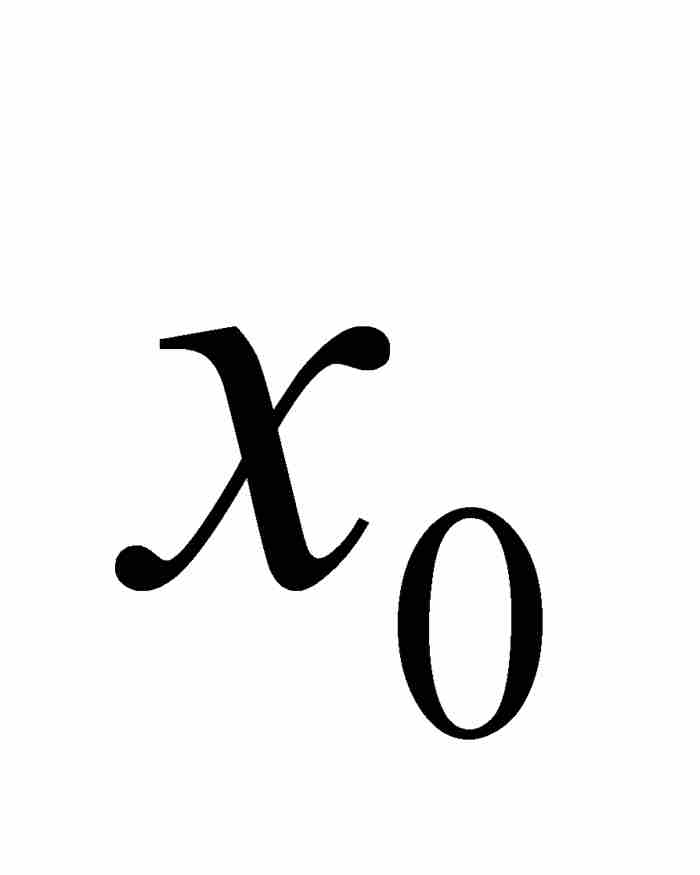顯然滿足一次方程
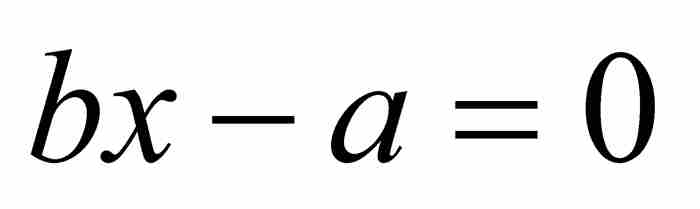，它的係數b和-a為整數。事實上，有理數恰好就是滿足整係數線性方程的那些代數數。
自然，並非每個代數數都是有理數，從前面提到的無理數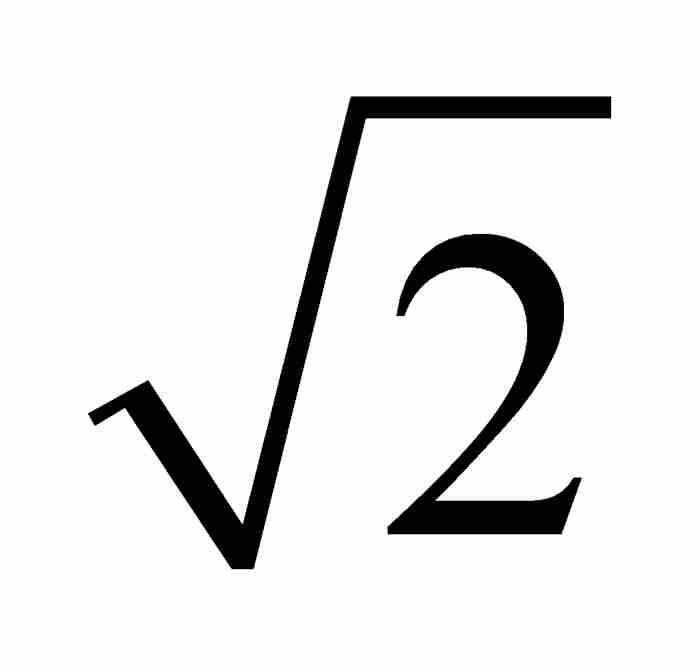
和
這樣的代數數中，我們清楚地看出這一點。因此，代數數代表著有理數的某種擴充，其中取消它們作為一次整係數多項式方程之解的條件，但是仍然保留多項式係數為整數的限制。
由此可見，如果超越數存在，它們必定隱藏在無理數中間。從古希臘起，人們就知道像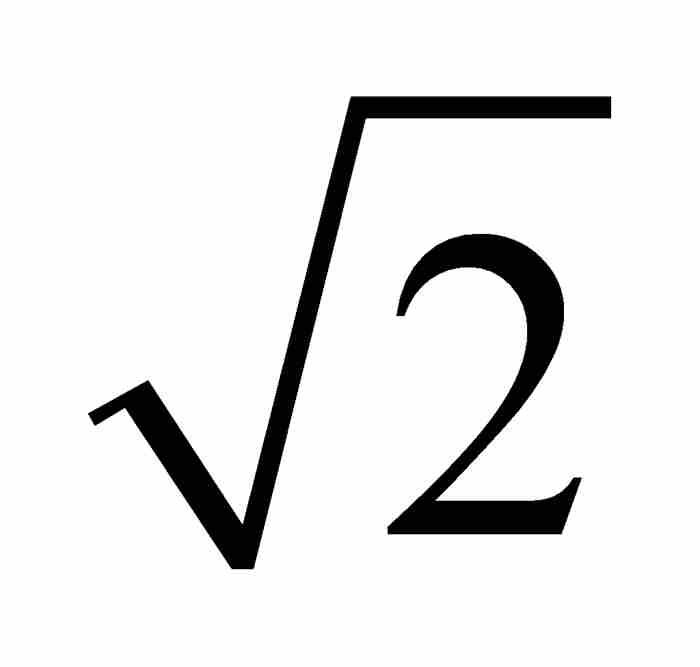
這樣的方程的根是無理數，而到18世紀末，e和π這兩個常數為無理數分別由歐拉於1737年和約翰·蘭伯特（1728—1777）於1768年證實。4 不過，同證明一個數是超越數比較起來，證明一個數是無理數要容易得多。
4 Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, pp. 459-460。
正如我們所提到的，歐拉曾經猜測log23是超越數，而勒讓德相信π也是超越數。5 然而，無論數學家們的信念多麼強烈，卻未能找到證明。直到19世紀中後期，甚至沒有取得存在一個超越數的證明。到那時，依然有這樣的可能性，這種超越數或許就像那些「超越海豚」一樣，無非是臆想中的空中樓閣而已。
5 Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 593。
最終，法國數學家約瑟夫·劉維爾提供了超越數的一個例子。如今的大學生們可能從微分方程的斯圖姆 · 劉維爾理論或者從復分析中的劉維爾定理（「一個有界的整函數為常數」）記起他的名字。劉維爾在電學和熱力學這樣的應用科學領域也作出了重大貢獻，同時他在1848年法國二月革命後的動盪年代投身政治活動，並且被選為法蘭西議會議員，活躍在一個完全不同的舞台上。此外，他還創辦了數學史上一本最具影響力的雜誌，這本雜誌原名為《純粹數學與應用數學雜誌》，但是人們通常簡單地稱之為《劉維爾雜誌》。他主編這本雜誌長達39年。劉維爾採用這種方式擔負起向整個歐洲以及世界各地的同行傳播數學思想的責任。6
6 劉維爾的這些工作以及他在其他方面的工作，在Jesper Lutzen所寫的科學家傳記Joseph Liouville 1809—1882: Master of Pure and Applied Mathematics (Springer-Verlag, 1990)中有詳盡論述。
在實分析領域，劉維爾以其兩項重大發現而被人們永誌不忘。第一，他證明了某些初等函數不可能存在初等原函數。任何學習過微積分的人都會記起運用一些巧妙的方法求不定積分。雖然這樣的方法不再像以往那樣是人們孜孜以求的，但是微積分教程仍然講述諸如分部積分法和部分分式積分法一類的方法，以便使我們能夠計算像
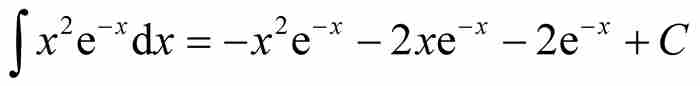
這樣的原函數，或者像
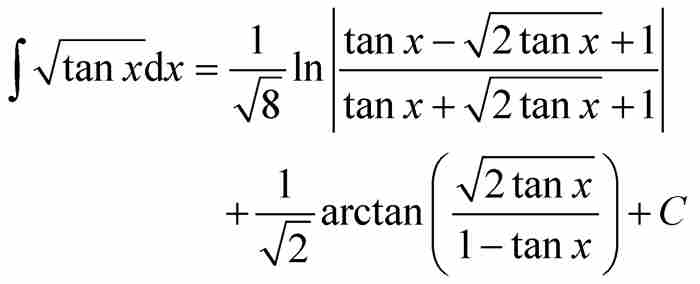
這種遠非不言自明的原函數。請注意，在這兩種情況下，被積函數和它們的原函數都是由標準歐拉函數集中的代數函數、三角函數、對數函數以及它們的反函數構成的。這樣的積分都是原函數為「初等」函數的「初等」積分。
可惜的是，即使最勤奮的求積者，當他們欲求作為簡單函數的有限組合的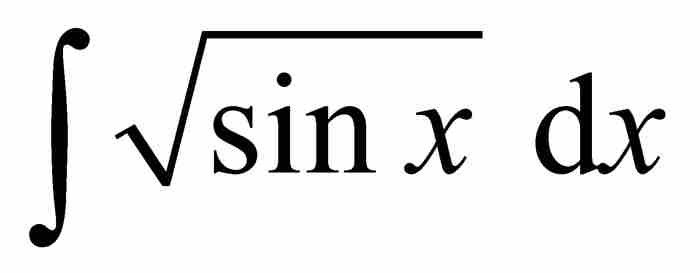
時，都會陷入困境。劉維爾找到了這個問題的原因。他在1835年的一篇文章中，證明了為什麼某些積分不可能具備最終形式的答案。他寫道，例如，「人們憑借我們的方法，很容易確信積分
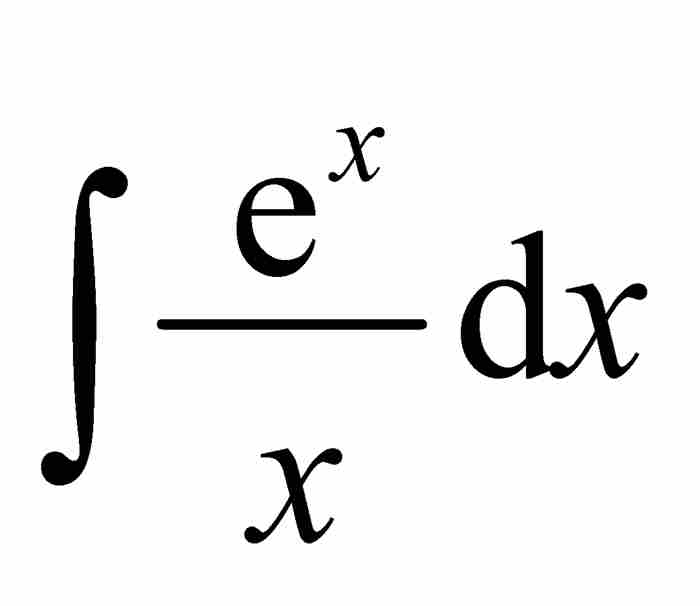不可能存在有限形式的原函數，而這個積分曾使幾何學家們忙得不可開交」。7 從此，簡單函數必然存在簡單原函數的希望化為泡影。
7 E. Hairer and G. Wanner, Analysis by Its History, Springer-Verlag, 1996, p. 125。
我們在這一章的目標是考察劉維爾的另外一項重大的貢獻，那就是存在超越數的證明。他的最初證明是在1844年給出的，不過他在1851年的一篇經典性論文中對結果作了改進和簡化（這篇論文自然是發表在他創辦的雜誌上），我們從中摘出證明。8 在劉維爾給出他的聞所未聞的超越數例子之前，他必須首先證明一個重要的不等式，這個不等式涉及代數數無理數同它們鄰近的有理數之間的關係。
8 J. Liouville, 「Sur des classes tres-etendues de quantites don't la valeur n'est ni algebrique, ni meme reductible a des irrationnelles algebriques」, Journal de mathematiques pures et appliques, vol. 16 (1851), pp. 133-142。
劉維爾不等式
正如我們指出的那樣，如果一個實數是某個整係數多項式方程的解，那麼它就是一個代數數。但是，這樣一個方程的任何解，都是無限個方程的解。例如，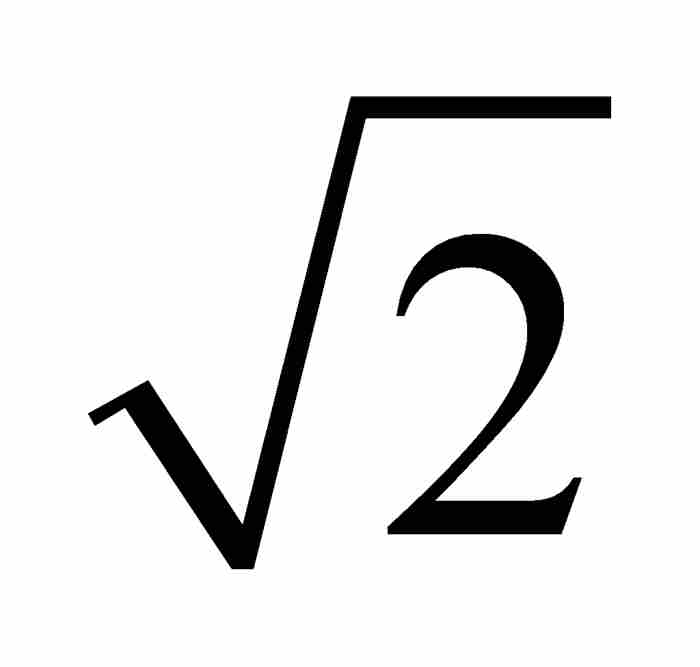
是二次方程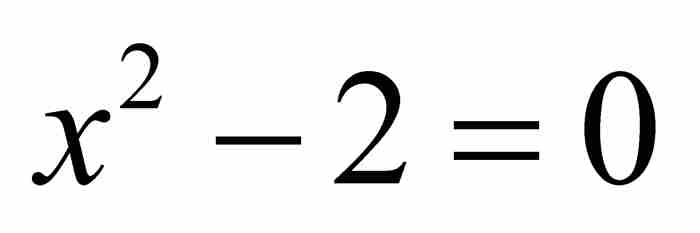
的解，它又是三次方程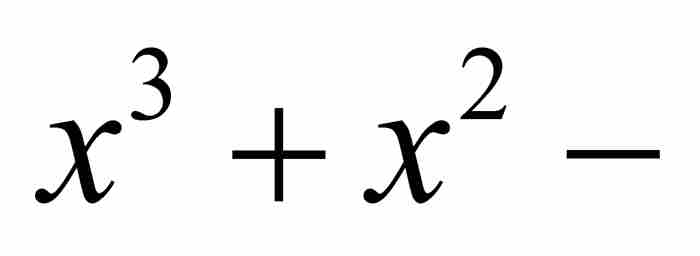
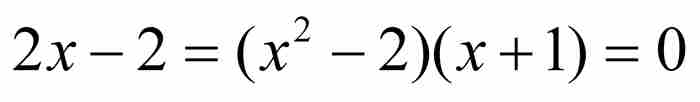的解，同樣也是四次方程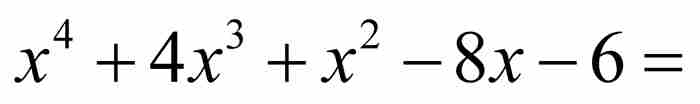
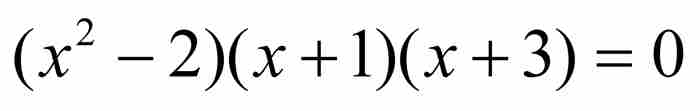的解，等等。於是，我們首先規定使用一個次數最低的多項式。所以，對於代數數
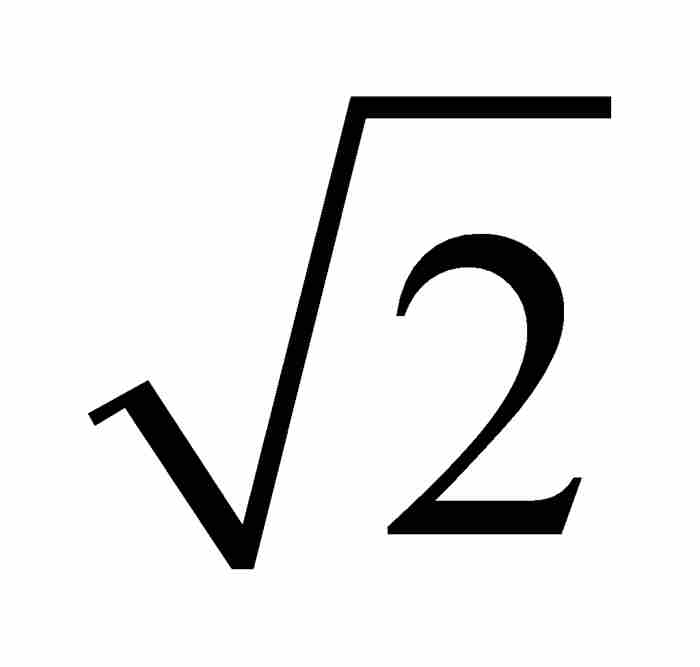而言，我們將採用上面的二次式而不是次數更高的同類多項式。
假定x0是一個無理數代數數。按照劉維爾的表示法，我們用
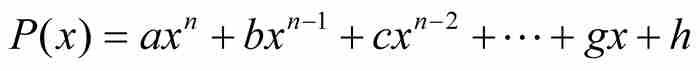（1）
表示它的次數最低的多項式，其中a, b, c, …, g, h為整數，n≥2（如果n=1，如像上面指出的那樣，那麼代數數是有理數）。由於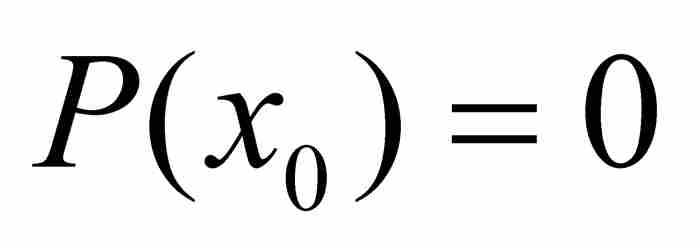
，用因式分解定理可以得到
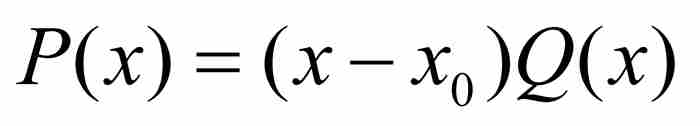（2）
其中Q(x)是一個n-1次多項式。劉維爾希望對於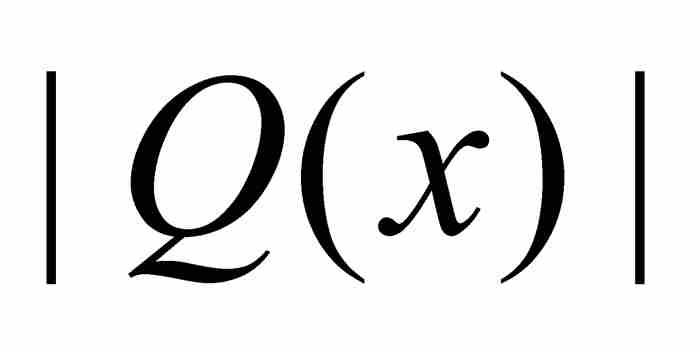
的值（至少對於Q在x0鄰近的x的值）確定一個上界。我們先給出他的證明，然後提供一個更簡單的替代證明。
劉維爾不等式 如果x0是次數最低的整係數多項式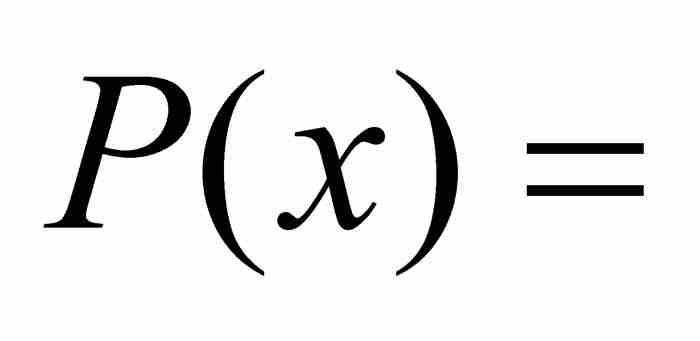
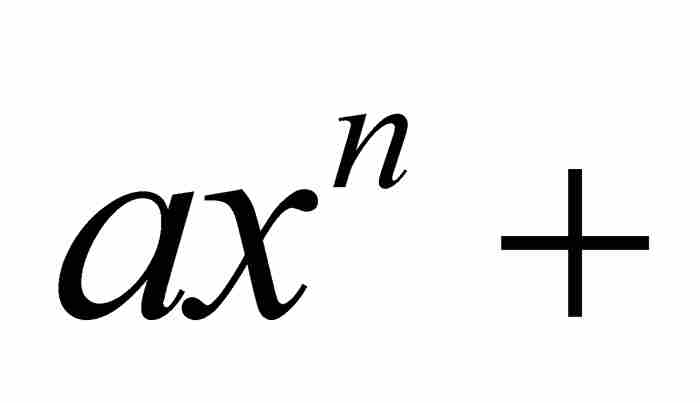
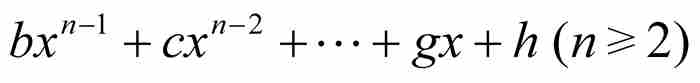的一個無理數代數數，那麼存在這樣一個實數A>0，只要p/q是區間
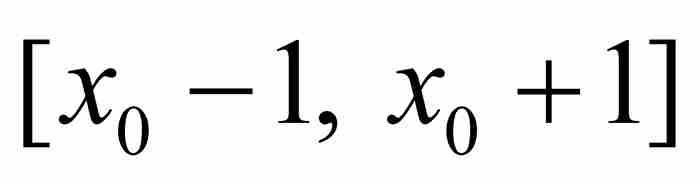內的一個有理數，就有
。
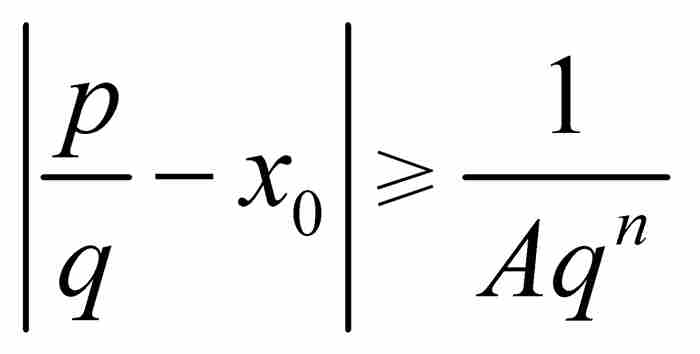證明 這個不等式的證明有其獨特之處，我們從式（2）引入的實係數多項式Q(x)著手。Q在任何有限閉區間上是連續的，因而是有界的，所以存在一個A>0，對於區間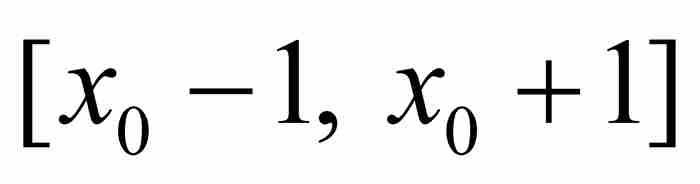
內的所有x，滿足
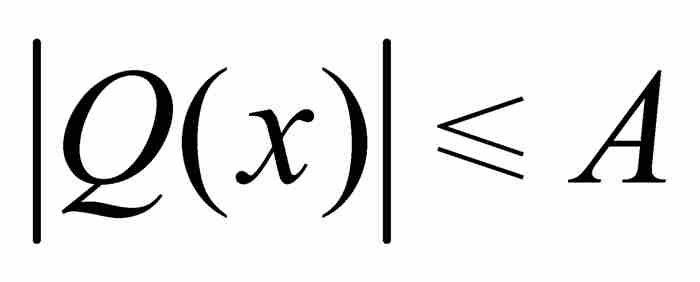（3）
現在考慮區間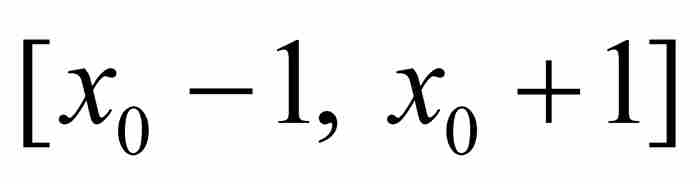
內的任何一個有理數p/q，其中我們要求這個有理數是最簡形式，並且分母為正整數（即q≥1）。由式（3）看出
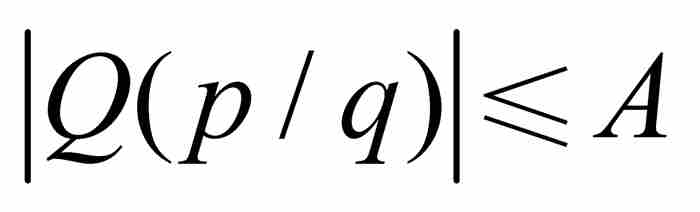，同時可以斷言
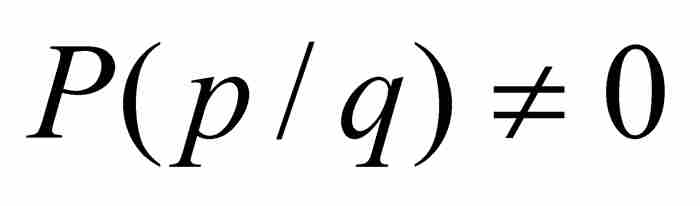，因為在相反的情況下能夠分解因式，得到
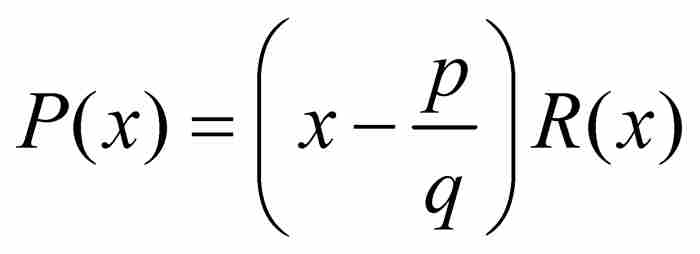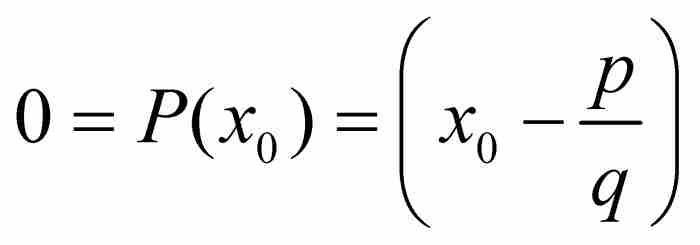
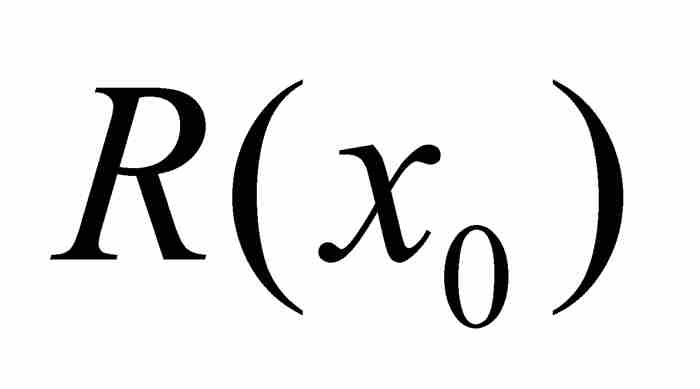，並且可以證明R(x)是一個n-1次整係數多項式。於是有
，並且有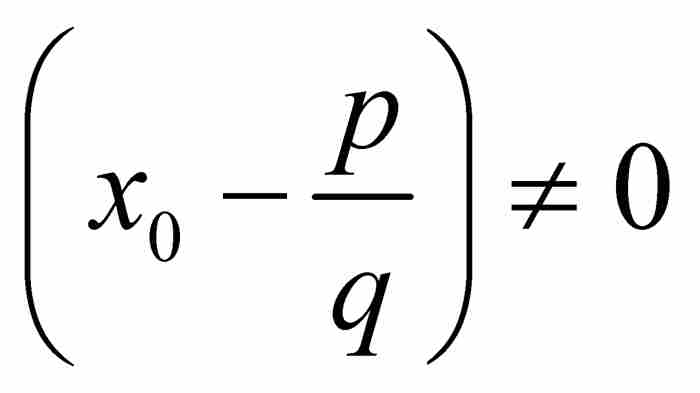
（因為有理數p/q不同於無理數x0），我們由此斷定
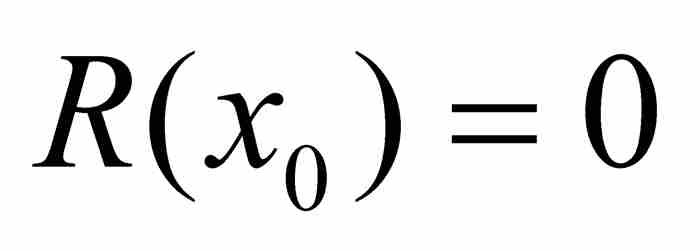。但是，這使x0成為
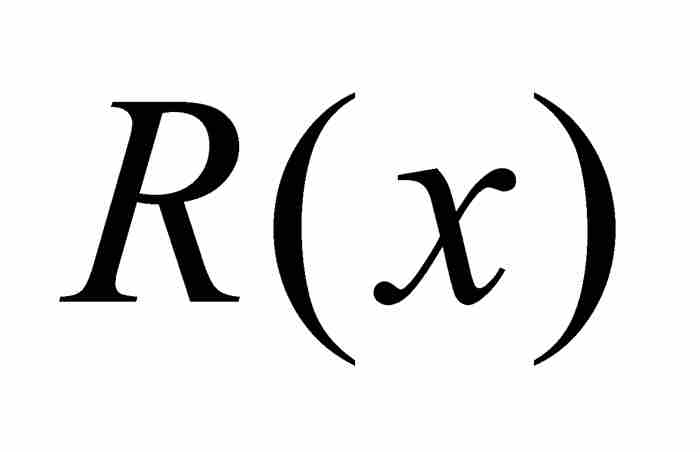的一個根，而R是次數小於P的一個整係數多項式，違反P是最低次多項式這個假定條件。這樣推出p/q不是
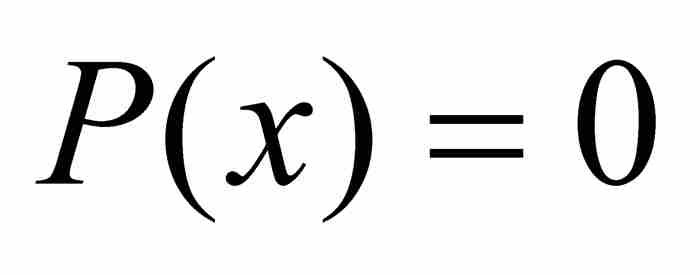的根。
劉維爾回到式（1）中的最低次多項式，並且給出定義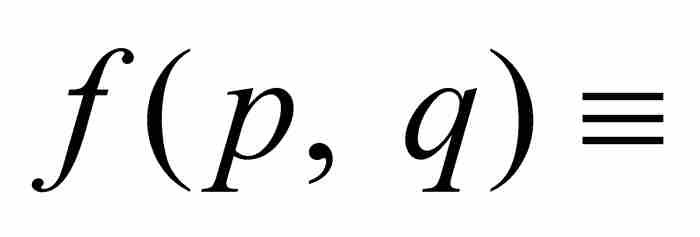
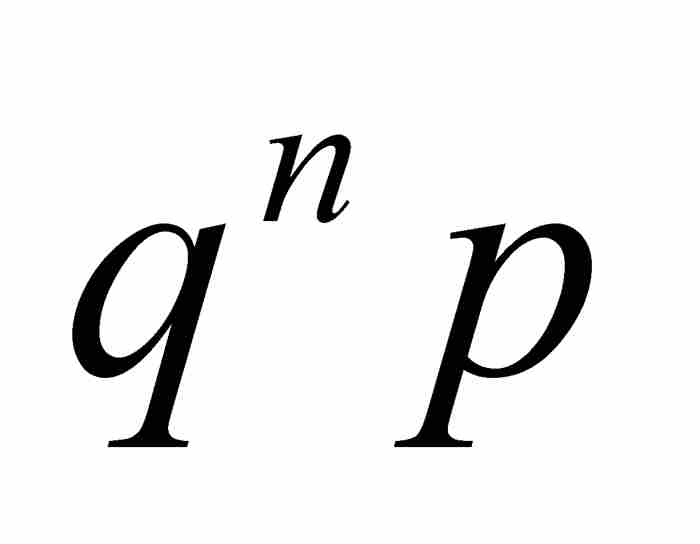
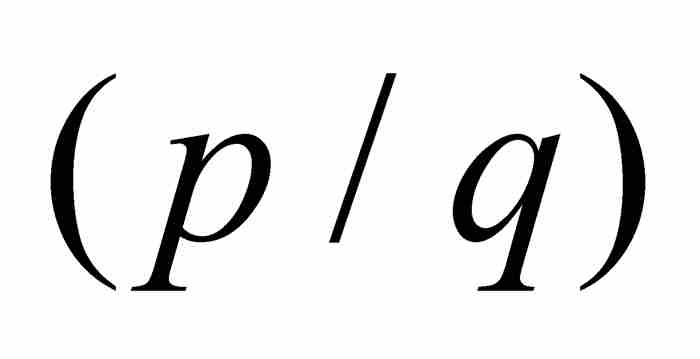。請注意，
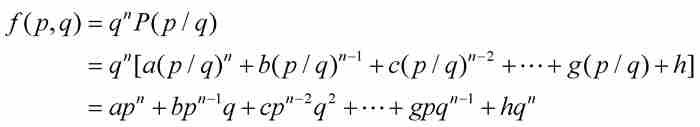（4）
他從式（4）作出兩條簡單然而具有說服力的說明。
第一，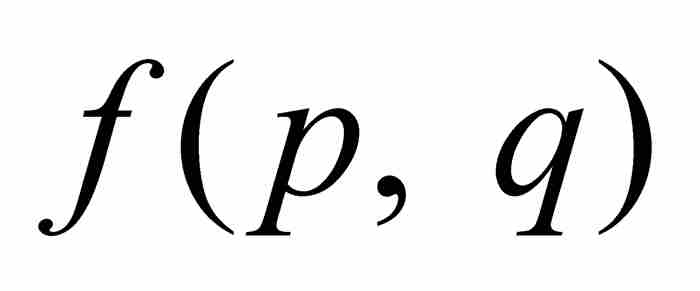
是一個整數，因為在其表達式中a, b, c, …, g，h以及p和q都是整數。第二，
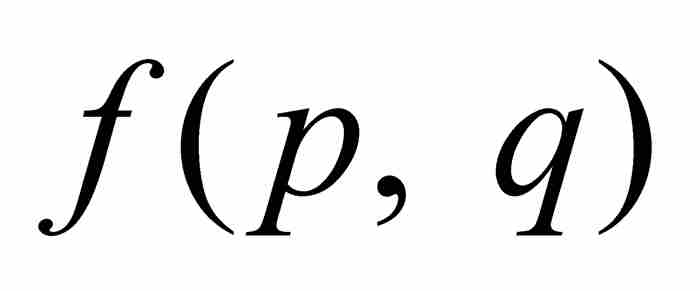不會為零，若不然，如果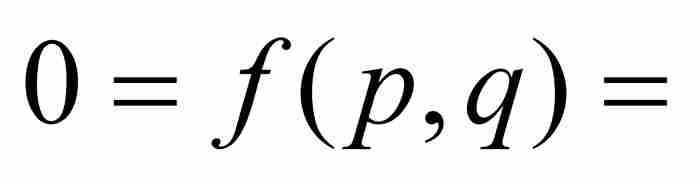
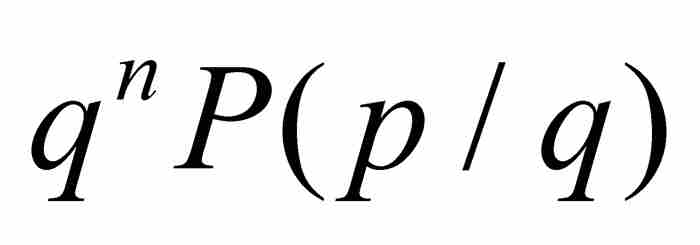，那麼就有
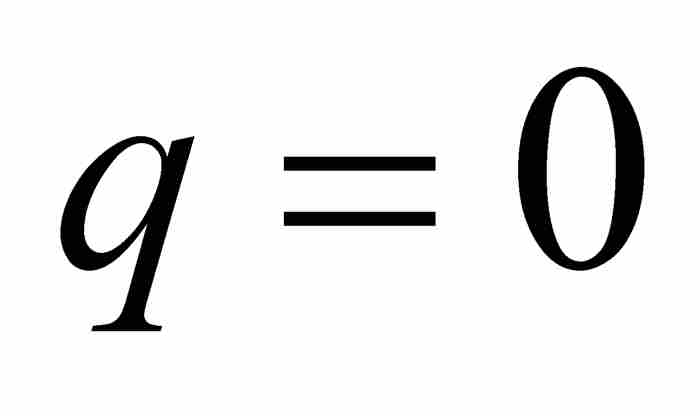或者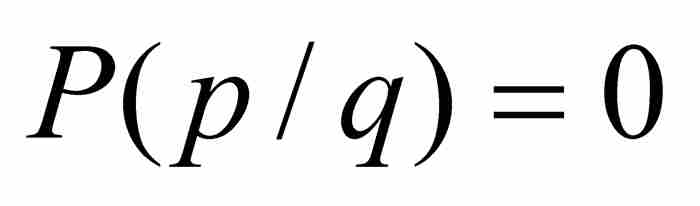
。前一種情況是不可能出現的，因為q是一個分母；至於後一種情況，從上面的討論看出同樣是不可能的。因此，劉維爾知道
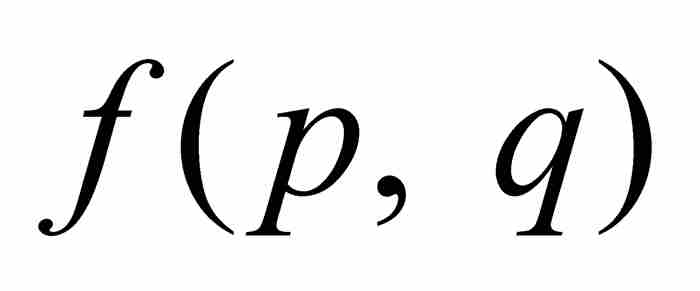是一個非零整數，他由此推出
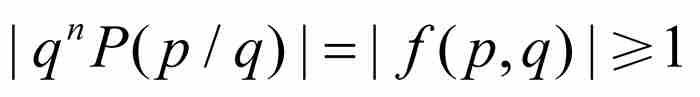（5）
定理證明的剩餘部分很快就會得到。根據式(3)和式(5)以及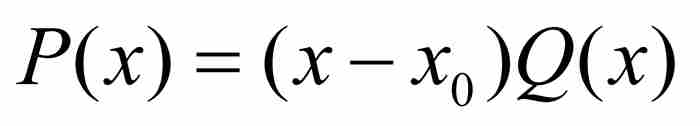
，他斷定
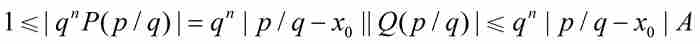
因此
，而定理的證明得以完成。
在劉維爾的證明中，不等式所起的作用是引人矚目的。所以人們有時把現代分析學稱為「不等式的科學」，這是對分析學特徵的恰如其分的表述，並且隨著這個世紀的前進，這個特徵日益顯現出來。
我們前面說過對劉維爾定理給出一種替代證明。這一次，柯西中值定理在證明中扮演主角。1
1 這個證明是從George Simmons, Calculus Gems, McGraw-Hill, 1992, pp. 288-289改寫成的。
我們把劉維爾不等式重述如下，然後給出新的證明。
劉維爾不等式 如果x0是具有最低次數的整係數多項式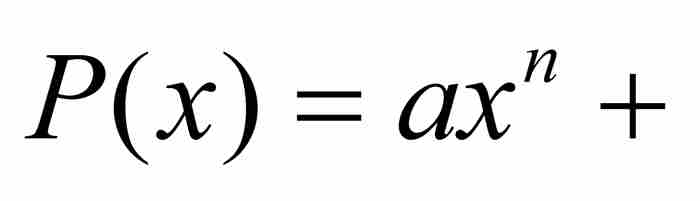
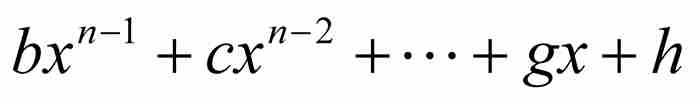和次數n≥2的一個無理數代數數，那麼存在這樣一個實數
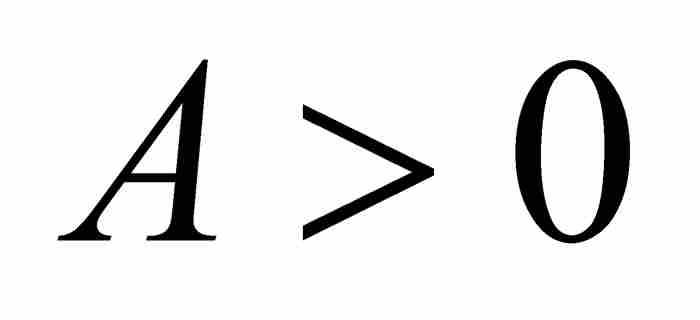，只要p/q為區間
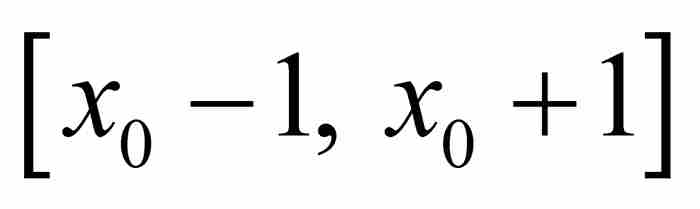內的一個有理數，就有
。
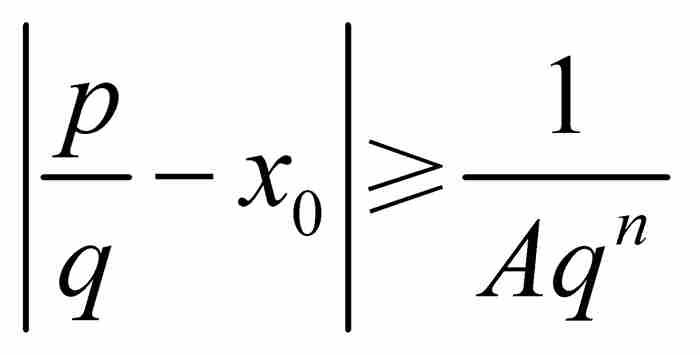證明 對多項式P求導，我們得到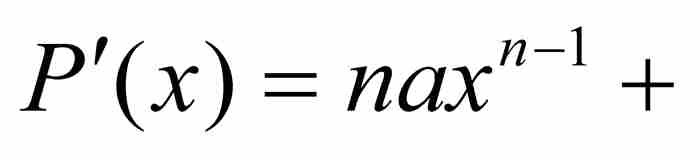
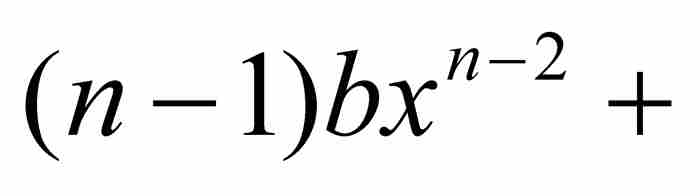
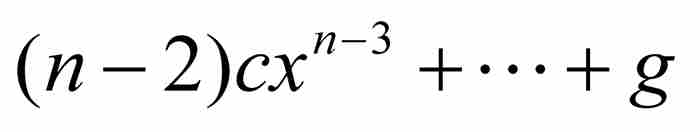。這個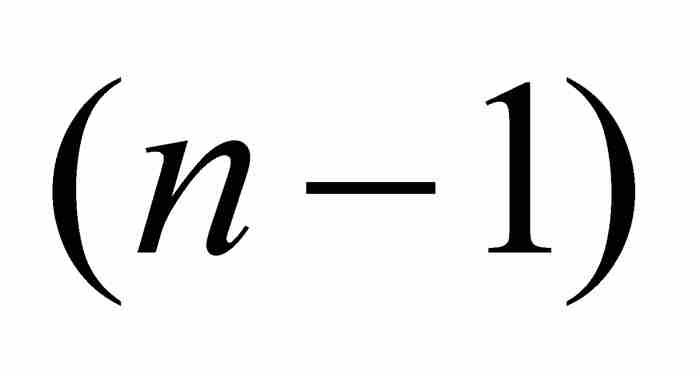
次多項式在區間
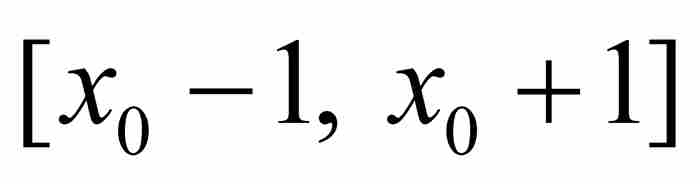上是有界的，所以存在一個
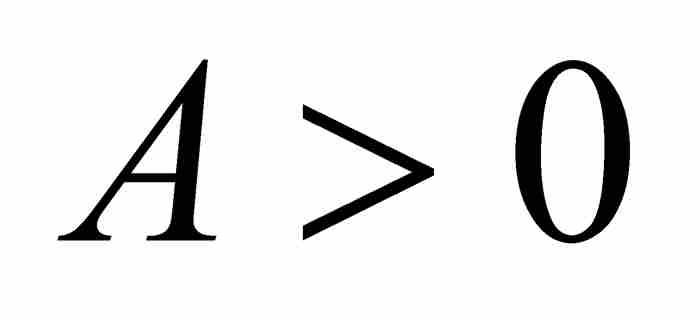，使得
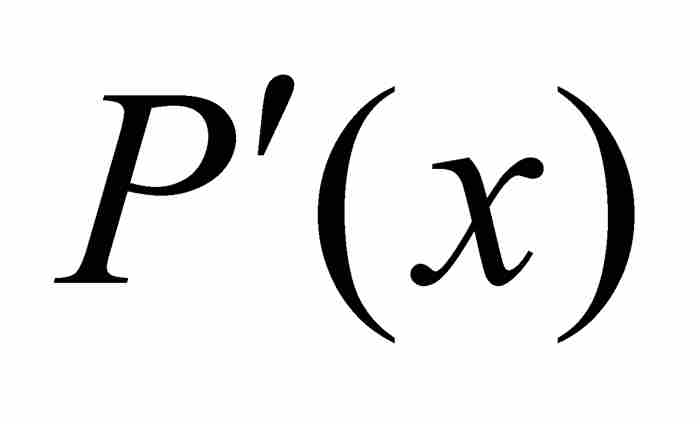在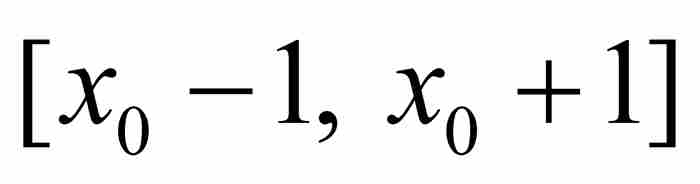
上以A為界，即對於所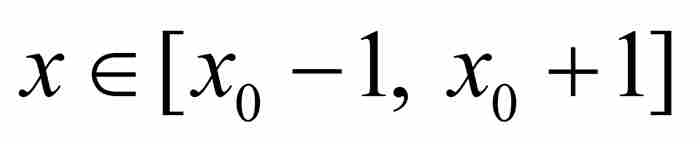有
有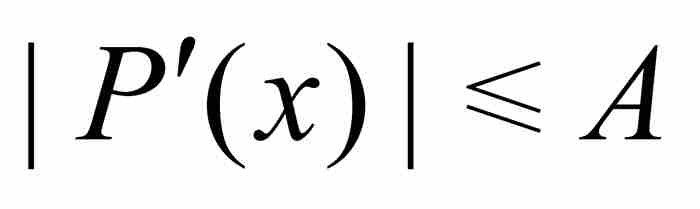
。令p/q是
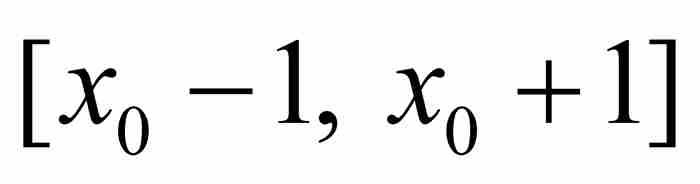內的一個有理數，並且對P應用柯西中值定理，可知在
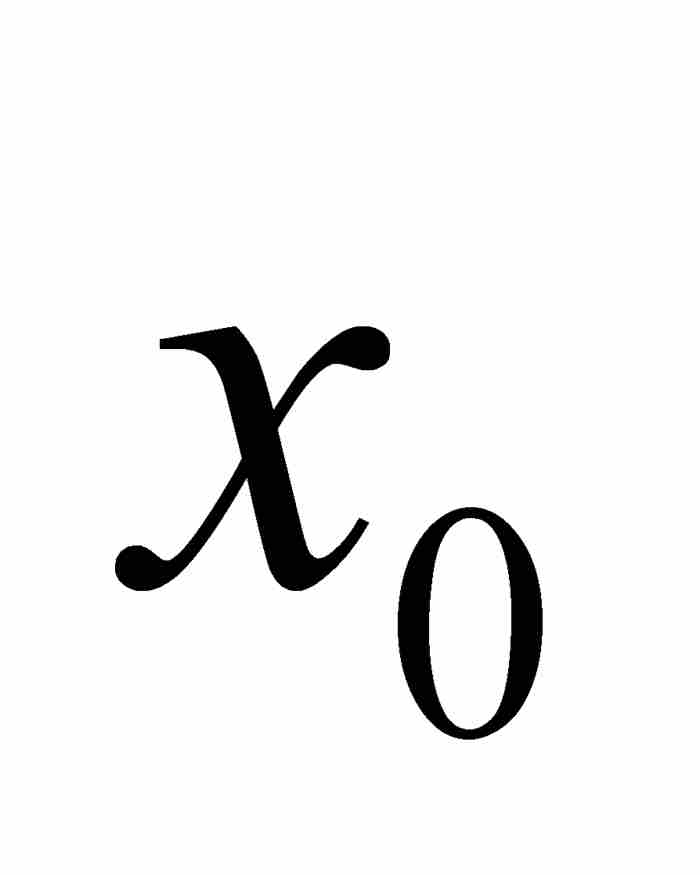和 p/q之間存在一點c，滿足
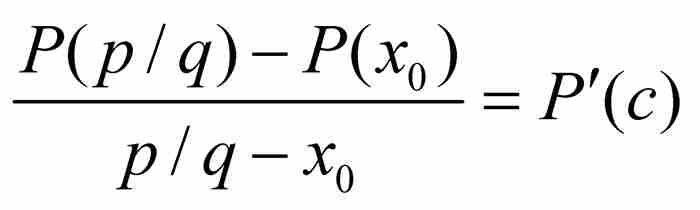（6）
已知
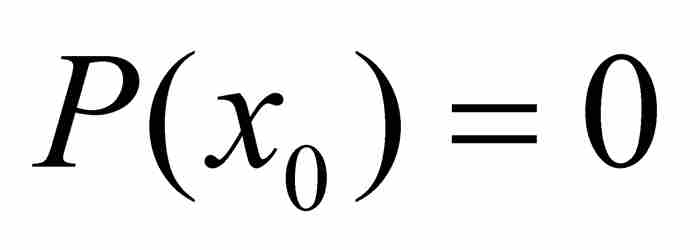，而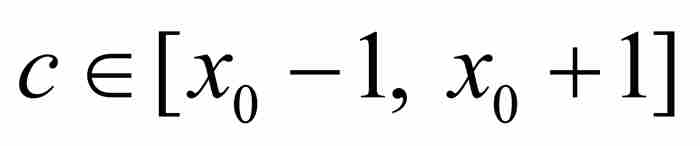
，由式（6）看出
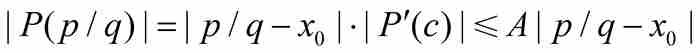
由此得到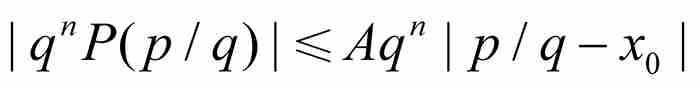
。但是，正如前面指出的那樣，
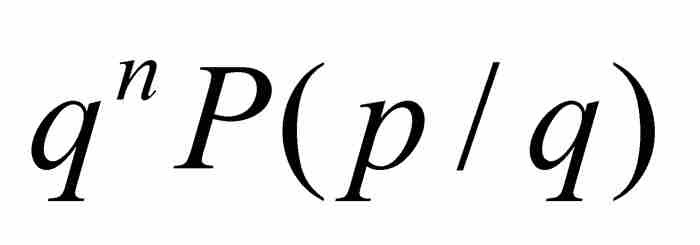是一個非零整數，所以
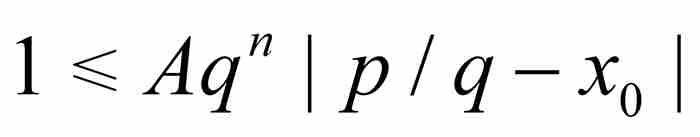。這就推出劉維爾不等式。
在此，舉一個例子或許有助於理解。我們考慮無理數代數數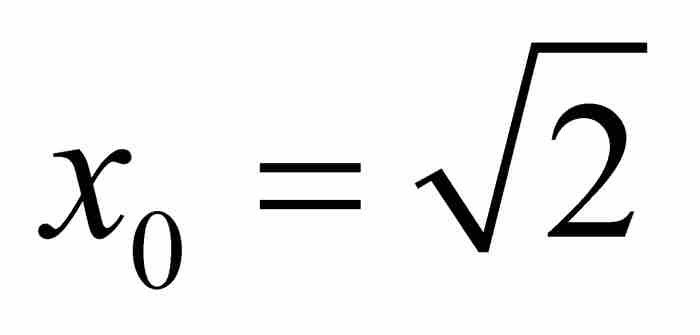
。這時最低次多項式為
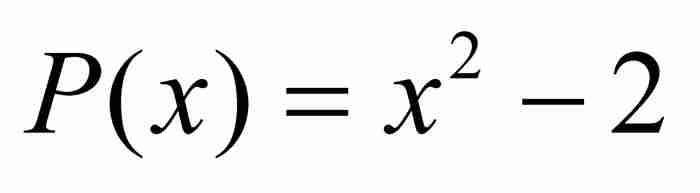，它的導數是
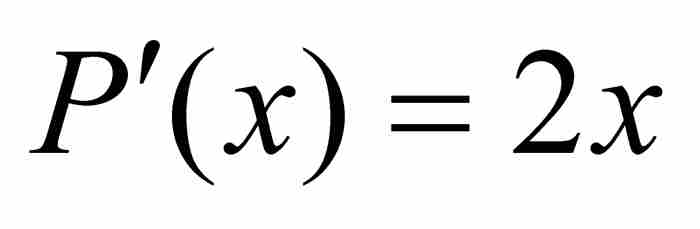。顯然，在區間
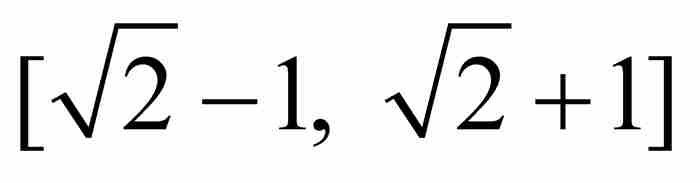上
以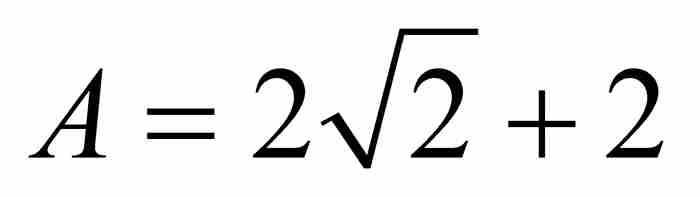
為界。劉維爾不等式表明，如果p/q是這個閉區間內的任何有理數，那麼
。
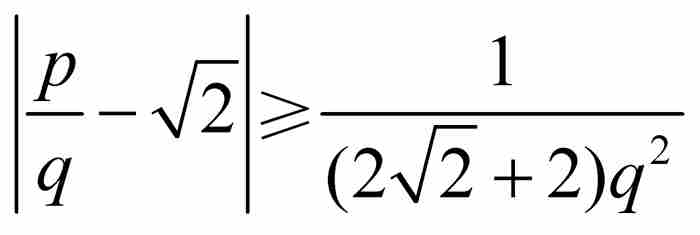這一點可望從數值趨勢上得到證實，例如，對於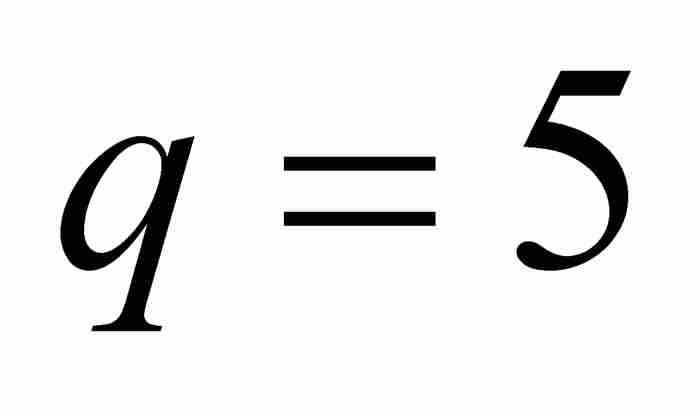
的情形，不等式變為
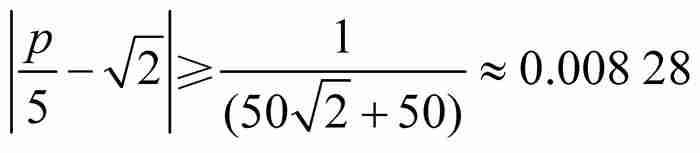。然後，我們檢驗區間
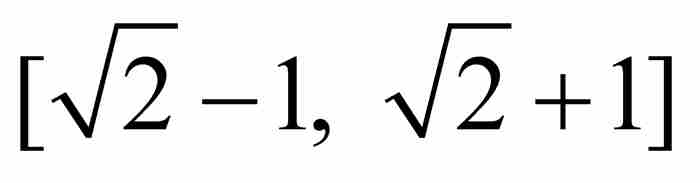內所有「1/5」處的點。所幸這樣的分數僅有10個，而且它們全部滿足劉維爾不等式：
p/5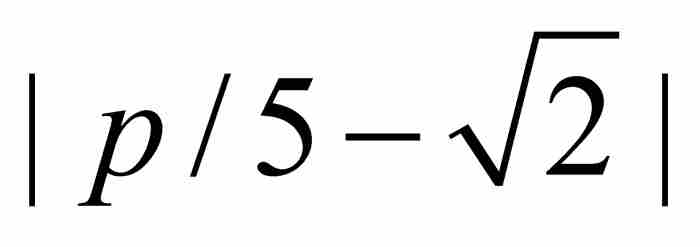
----------------------------------- 3/5=0.600.8142 4/5=0.800.6142 5/5=1.000.4142 6/5=1.200.2142 7/5=1.400.0142 8/5=1.600.1858 9/5=1.800.385810/5=2.000.585811/5=2.200.785812/5=2.400.9858
這個例子同時也暗示：通常我們可以取消要求p/q接近x0的限制。就是說，我們指定A*為大於1和A的數，其中A是像上面那樣確定的。如果p/q是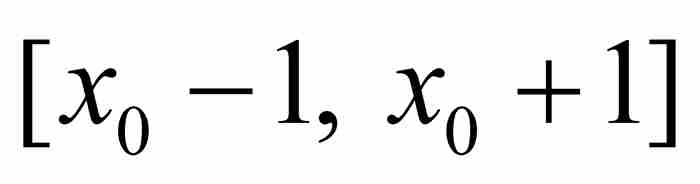
內的一個有理數，那麼由於A*≥A而有
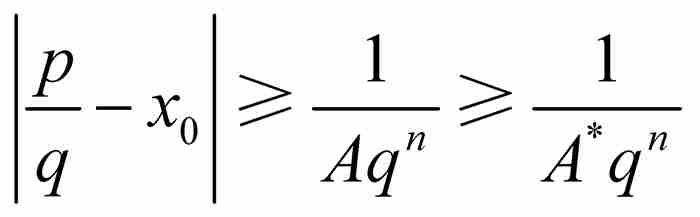
另一方面，如果p/q是區間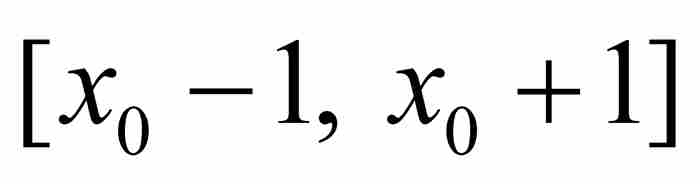
之外的一個有理數，那麼由於A*≥1和q≥1，同樣有
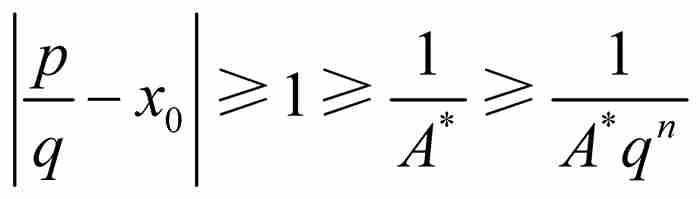。最後這項結果說明，存在一個A* > 0滿足
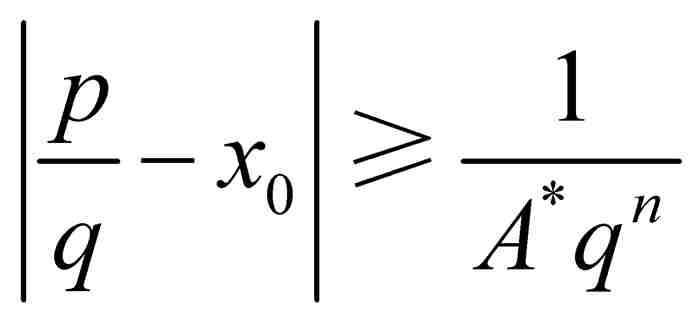，而同p/q對x0的接近程度無關。
通俗地講，劉維爾不等式向我們表明，有理數作為無理數代數數的鄰居，其數量是少得可憐的，因為在一個無理數x0同任何有理數p/q之間必定至少存在一個大小為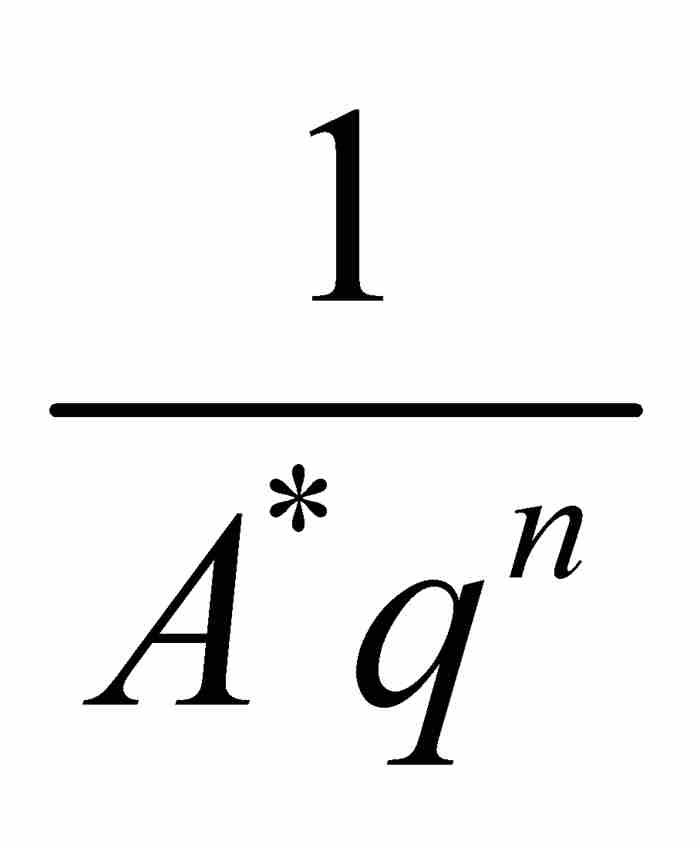
的空隙。我們很難想像劉維爾是怎樣注意到這一點的。他走到了這一步，並且提供了一個巧妙的證明，這是他的卓越數學才能的一次展現。然而，倘若他不再邁出下面這一步，這一切也許早已被人們遺忘：他利用他獲得的結果找到了世界上第一個超越數。
劉維爾超越數
我們首先提出關於推理策略的一個詞彙——「不相容」。劉維爾找到的是一個同上述不等式的結論不相容的無理數。這個無理數因而違反劉維爾不等式的假定，這就意味著它不是代數數。只要劉維爾能夠完成這項艱巨的任務，他就捕捉到一個特定的超越數。令人非常吃驚的是，他恰好做到了這一點。1
1 J. Liouville, 「Sur des classes tres-etendues de quantites don't la valeur n'est ni algebrique, ni meme reductible a des irrationnelles algebriques」, Journal de mathematiques pures et appliques, vol. 16 (1851), pp. 133-142。
定理 實數
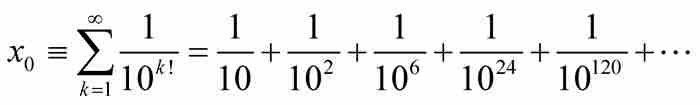
是超越數。
證明 有三個問題有待解決，我們依次一步處理一個問題。
第一步，我們斷言定義x0的級數是收斂的。這個結論很容易從判別級數收斂的比較檢驗法推出。也就是說，
保證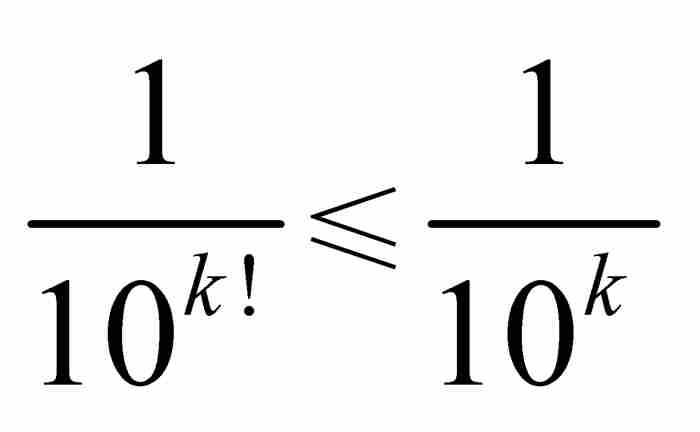
，而這個條件使級數
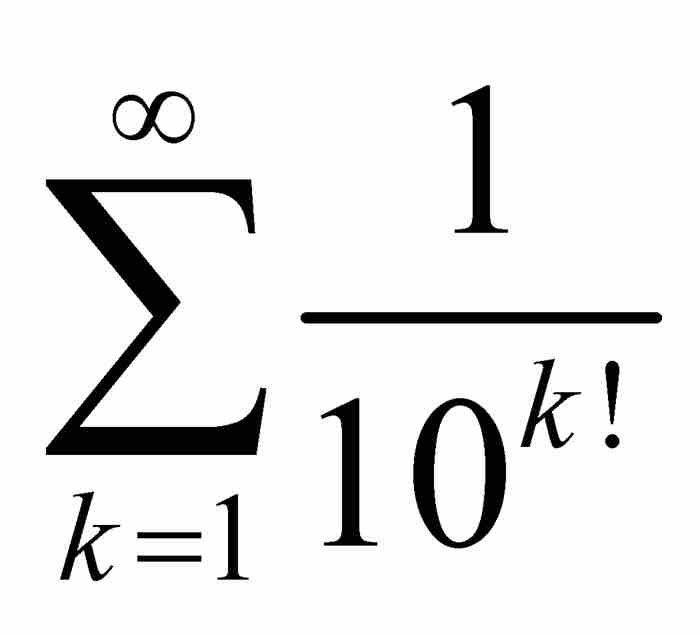成為收斂級數，因為
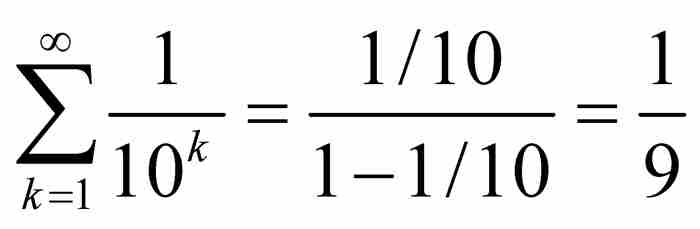是收斂級數。簡而言之，x0是一個實數。
第二步，我們斷言x0是無理數。這一點是明顯的，因為它的十進制小數表示為0.110 001 000 000 0…，其中的非零位分別是由1佔據的小數後的第1位，第2位，第6位，第24位，第120位，等等，這些日漸孤單的1由越來越長的一串0分隔開來。顯而易見，在這種十進制小數的展開式中，沒有一段有限的數字是重複的，所以x0是無理數。
最後一步，證明劉維爾定義的數是超越數。這也是最困難的一步。為此，我們反過來假定x0是一個代數數無理數，它具有次數為n≥2的最低次多項式。根據劉維爾不等式，必定存在這樣一個A* > 0，使得對於任意有理數p/q，有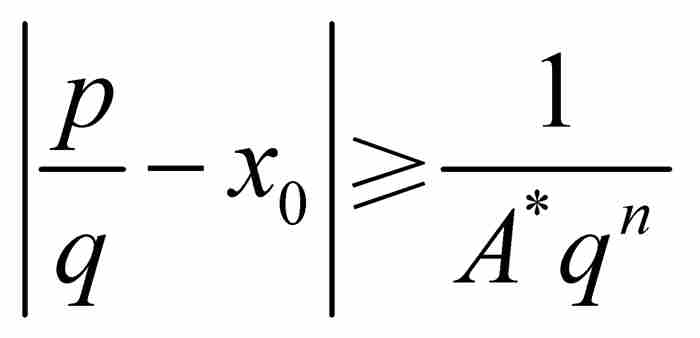
，因此，
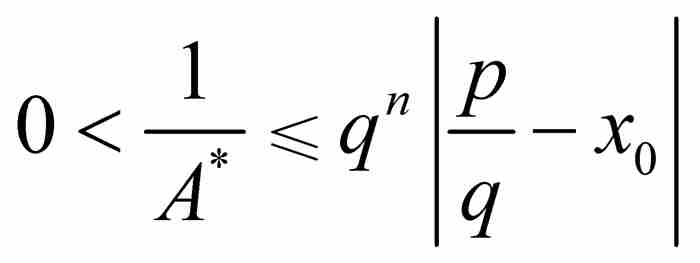（7）
我們現在選擇一個任意的自然數m > n，並且考察部分和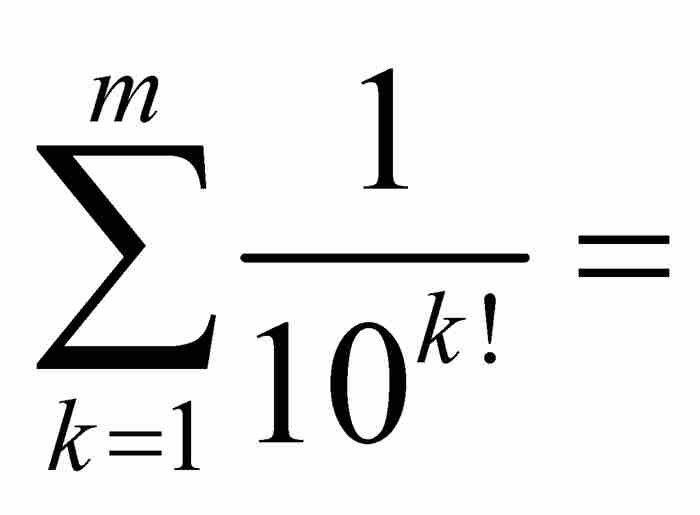
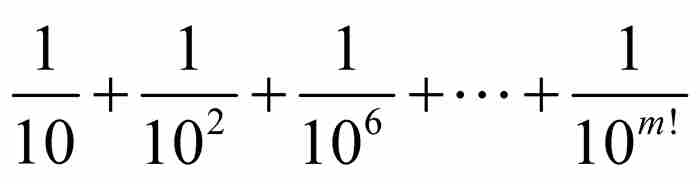。如果合併這些分式，它們的公分母將是10m!，所以我們可以把這個和式寫成
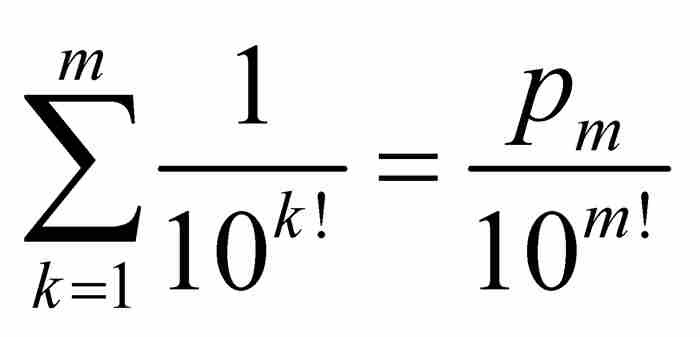，其中pm是一個自然數。因此，
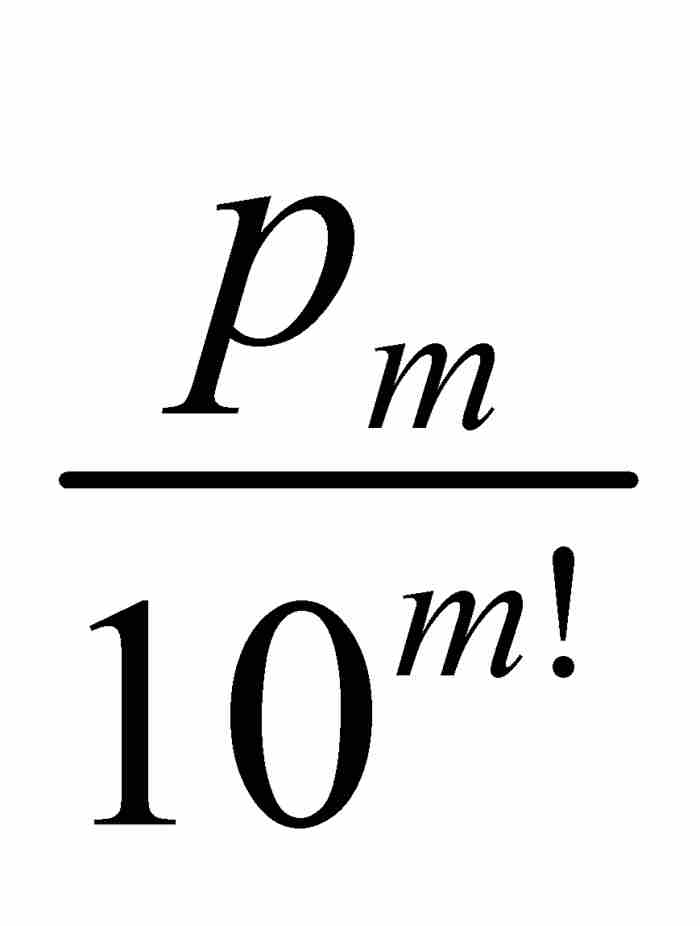當然是有理數。
把這個數同x0比較，我們看出
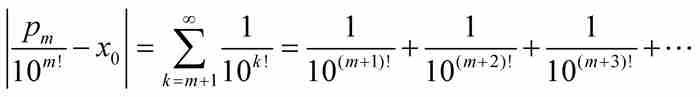
由歸納法證實，對於任何自然數r≥1，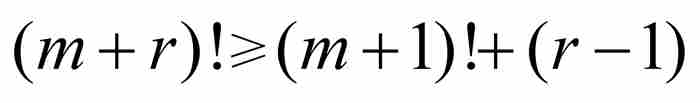
成立，所以有
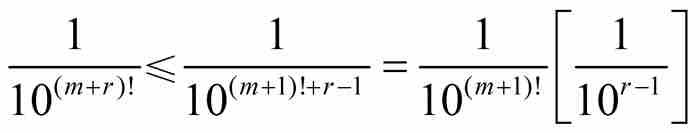。結果得到
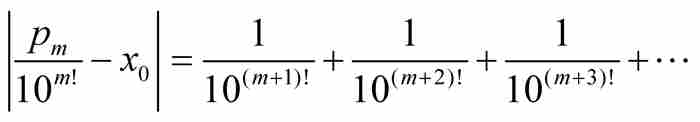
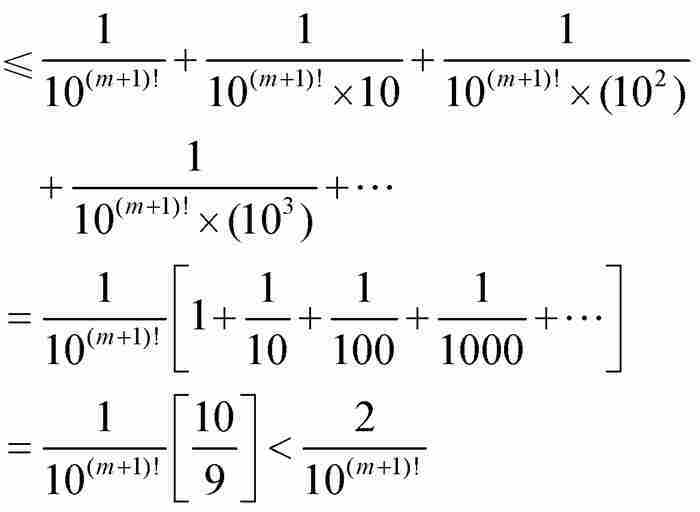
（8）
這樣立即導致一個矛盾，因為
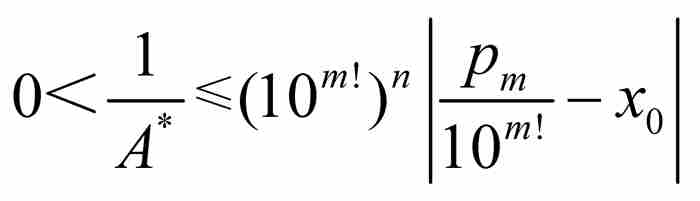（由式（7））
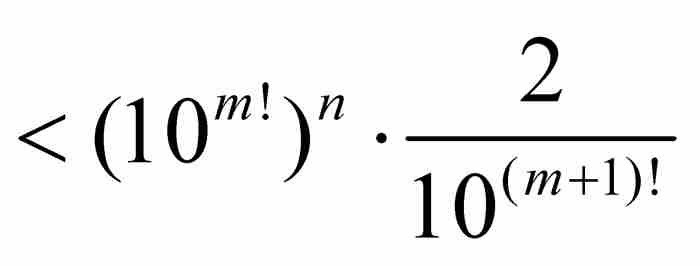（由式（8））
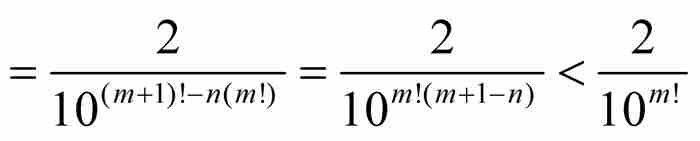
其中最後一步推導是由於m > n蘊含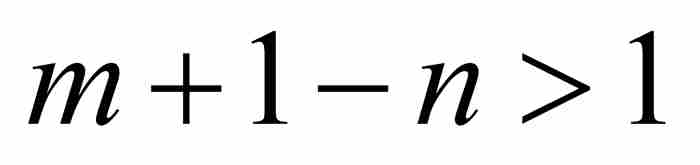
。
這一長串不等式表明，就上面引入的A*的值而言，對於所有m > n，我們有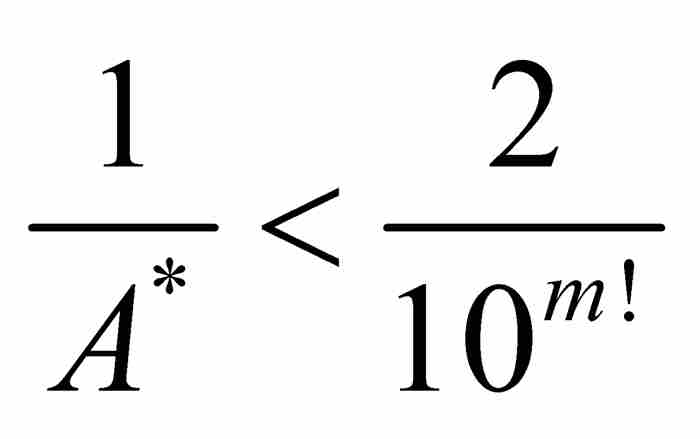
，或者簡單地說，對於所有m > n，有2 A* > 10m!。這樣一個不等式是荒謬的，因為2 A*是一個固定的數，而10m!當m增大時趨向無窮大。劉維爾（最終）導出一個矛盾。
至此，可能需要略微提醒一下讀者出現了什麼矛盾。已經假定無理數x0是一個代數數。然而，最終得到的卻是另外一種結果，所以只有一種可能：x0必定是超越數。這樣一個數的存在，就是約瑟夫·劉維爾試圖證明的結論。
劉維爾在1851年發表的一篇文章中指出，儘管許多人推測超越數的存在，「我不相信已經給出過任何證明」。2 如今，終於有了一個證明。
2 J. Liouville, 「Sur des classes tres-etendues de quantites don't la valeur n'est ni algebrique, ni meme reductible a des irrationnelles algebriques」, Journal de mathematiques pures et appliques, vol. 16 (1851), p. 140。
說來奇怪，對於取得的這個成就，劉維爾認為還不能算是完全成功，因為他的初衷是希望證明e是一個超越數。3 像劉維爾所做的那樣，構造一個數，然後證明它是超越數，這是一回事；而對於「已經存在的」如e那樣的數，證明它是超越數，則是另一回事。對於這一點，Eric Temple Bell以其特有的鑒別力作出下面的評論：
證明一個特定的猜測，如像e或π是超越數或者不是超越數，同構造一類無窮的超越數相比，是困難得多的問題：……在這種情況下，被猜測的數是主導者，而數學家只能聽命於它。4
3 Joseph Liouville 1809—1882: Master of Pure and Applied Mathematics (Springer-Verlag, 1990), pp. 79-81。
4 Eric Temple Bell, Men of Mathematics, Simon & Schuster, 1937, p. 463。
我們姑且可以這樣說，劉維爾證明了過去無人關心的一個數的超越性，但是對於無處不在的常數e未能給出同樣的證明，而這個數的超越性又是使數學家們魂牽夢繞的。超越數是在劉維爾之前的先軀們徒勞地尋找了一百年的東西，當他找到超越數後，如果仍然對他貼上失敗的標籤，無疑是荒唐可笑的。
劉維爾最初提出的目標很快將由他的繼承者們實現。在1873年，查爾斯·埃爾米特（1822—1901）證明了e確實是一個超越數。九年之後，費爾登蘭德·林德曼（1852—1939）對 π 證明了同樣的結果。眾所周知，林德曼曾經證實用圓規和直尺求圓的面積是不可能的，這是古希臘人提出的著名的「化圓為方」問題，歷經幾千年而非幾十年或幾百年不得其解。5 在埃爾米特和林德曼的結果中，包含著令人歎為觀止的推理步驟，而這種推理是建立在劉維爾的開拓性研究工作之上的。
5 例如，參見William Dunham, Journey through Genius, Wiley, 1990, pp. 24 -26中的討論。
時至今日，確定某個給定的數是不是超越數，在數學中仍然屬於最困難的問題之列。在這方面已經取得了很大進展，很多重要的定理已經獲得證明；然而，據我們瞭解，仍然留下大量的盲區。在已經得到的巨大成就中，我們不能不提出阿什波維奇·蓋爾芳德（1906—1968）在1934年的證明，其中他一舉證實了一族完整的超越數。他證明，如果a是一個不同於0或1的代數數，而b是一個無理數代數數，那麼ab必定是超越數。這個深奧的結果，保證例如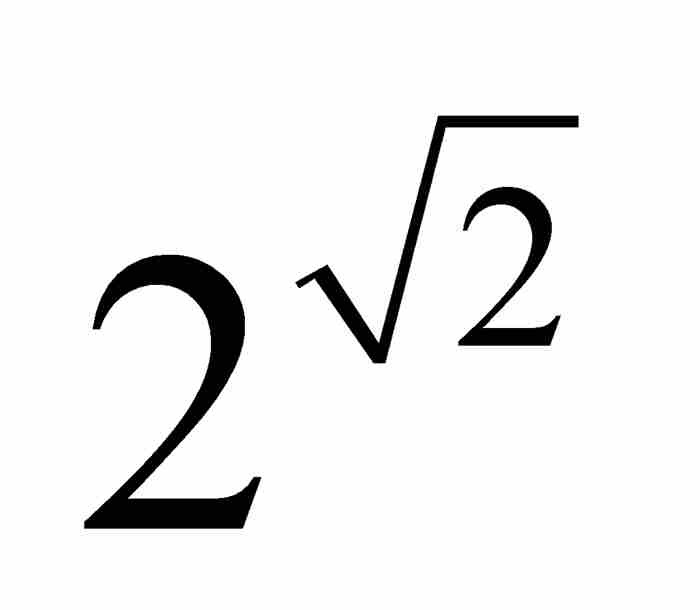
或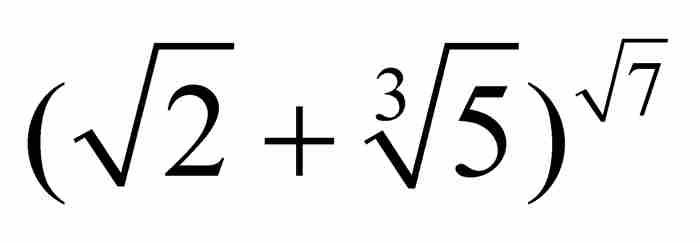
這樣的數是超越數。如今已經知道，在超越數候選者之列的還有eπ，ln(2)和sin(1)。
然而，直到寫作本書時，像 πe，ee和 ππ這樣一些看似「簡單的」數的性質尚有待證實。更為嚴重的是，儘管數學家們對 π + e和 π × e是超越數深信不疑，但是尚無人給出實際證明。6 我們再重複一遍：證明一個數的超越性是非常非常困難的。
6 Andrei Shidlovskii, Transcendental Numbers, de Gruyter, 1989, p. 442。
回到本章的主題，我們看出，到19世紀中期數學家們已經走了多遠。劉維爾在處理不等式時表現出的學術才華以及他在如何攻克如此困難的問題方面的廣闊視野，的確是令人難忘的。分析學已經步入它的成熟期。
在第11章將要證明關於實數完備性的一個里程碑式的定理，劉維爾這裡的證明將同那個定理的證明形成鮮明的對照。在那裡我們將會看到格奧爾格·康托爾如何找到一條明顯的捷徑，僅做少量的工作就得到劉維爾的結論。康托爾以這種方式改變了數學分析的方向。劉維爾和康托爾的相互影響將是一筆巨大財富，昭示我們如何使數學的活力延續下去。
不過，暫時不得不把康托爾的工作擱置一下。我們的下一個目標是展現19世紀分析學所追求的嚴格性的終點：卡爾·魏爾斯特拉斯的數學以及分析學中最著名的反例。