不管是什麼樣的真理，
只要一經發現，就很容易被人理解。
重點在於，要去發現真理。
——伽利略·伽利萊
10.1 雙倉圖書館
10.1.1 入口
“唉 —— 累死了啦。”
“是這裡嗎？”
“嗯。”
現在正值春假，我和尤里、泰朵拉三個人來到了雙倉圖書館。雙倉圖書館是建在小山坡上的一座三層小樓，有一個圓圓的屋頂。我們從車站一路爬上山，迎面就看見了入口處的圖書館標誌。
圖書館裡面很開闊，像酒店的大堂一樣。抬頭望去，每一層都像迴廊一樣環繞著整個室內中庭。透過玻璃可以看見一排排的書架。柔軟的沙發擺放在各處，坐在上面的人們各自看著自己想看的書。四處漂浮著一種圖書館特有的氣息 —— 由很多很多圖書散發出來的氣息。
“我們去哪兒好？”泰朵拉四下張望。
“米爾嘉說有人會來告訴我們……”我說道。
這時，前台一位英俊的男士告訴了我們房間的位置。
“說是一樓的叫‘氯’的房間。”我在走廊裡一邊走著，一邊和她們說話。
“泰朵拉，剛才那個人真是帥得要命啊……”尤里說道。
“那個人應該是圖書管理員吧？”泰朵拉說道。
“他可沒戴結婚戒指呀！”
幾句話的工夫，居然連戒指都注意到了……啊，到了。
我推開了寫著 Chlorine 的門。
10.1.2 氯
“你們來啦。”米爾嘉說道。
“我說米爾嘉，這裡是哪兒啊？”我坐在椅子上，四下看了看整個房間。
房間中央有一張橢圓形的桌子，桌子周圍擺放著帶靠背的椅子。四面牆中有一面整個是一大塊白板，這讓房間看起來像個多功能會議室。房間的角落裡有內線電話跟書架。從寬敞的窗戶望出去，可以看到一片綠色，像是個庭園。
“這裡？是圖書館啊。”米爾嘉說道。
“我記得叫……雙倉圖書館吧？”泰朵拉坐下說道。
“對。雙倉博士的私立圖書館。”米爾嘉說道，“這裡有很多數理方面的藏書。也有很多房間像這間一樣，裡面有用來開會或討論的設備。據說這裡偶爾也會召開小型國際會議。雖說我只參加過幾次數學研究會，不過我覺得這裡確實很方便。”
誒？米爾嘉還參加過那種會議吶。
“米爾嘉大人，今天講什麼？”尤里問道。
“我們要花上一整天，一起‘用數學研究數學’。”
“用數學研究數學？”尤里不解。
“就是一起思考現代邏輯的出發點 —— 哥德爾不完備定理。要是我們去高中圖書室，會受很多限制，而且尤里你也去不了。”
“好高興喵！啊，對了對了，米爾嘉大人，請收下這個！”
尤里遞出一個小紙包，裡面包著點心。
“喔……那這個就拿來配下午茶吧。”
米爾嘉面向白板，拿出一支馬克筆。
“因為會講很多，所以我們先來列個大綱。”
◎ ◎ ◎
首先，我要講的是希爾伯特計劃。數學家希爾伯特想要給數學一個牢固的理論基礎，因而提出了希爾伯特計劃。
其次，我要整體講一下哥德爾不完備定理。哥德爾的不完備定理表明了希爾伯特計劃用當時的方針是無法實現的。在證明哥德爾不完備定理之前，我要講一下這個定理本身。
然後，就是仔細研究哥德爾不完備定理的證明。這裡會講很久，所以中途要吃個午飯，還有午後茶點。
最後是思考不完備定理的意義。關於不完備定理的負面評價很多，例如它破壞了希爾伯特計劃呀，表明了數學的界限啊，等等。然而，不完備定理是創造了現代邏輯基礎的定理。我們應該關注的是不完備定理具有的建設性意義。
那麼，我們就進入正題吧。
10.2 希爾伯特計劃
10.2.1 希爾伯特
戴維·希爾伯特是一位活躍在 19 世紀至 20 世紀初的數學領軍人物。他為了給數學建立一個堅實牢固的基礎而提出了希爾伯特計劃。這個計劃由以下三個階段構成。
-
導入形式系統
- 以“形式系統”來表示數學。
-
證明相容性
- 證明用於表示數學的形式系統“不存在矛盾”。
-
證明完備性
- 證明用於表示數學的形式系統是“完備的”。
我來依次說明這三個階段。
導入形式系統 —— 希爾伯特想要用形式系統來表示數學。數學是一門非常大的學問，涉及各種各樣的領域。不弄清楚“數學是什麼”，就不能建立起牢固的基礎。因此希爾伯特決定把數學視為形式系統。於是，他把邏輯公式定義為符號的序列，並在邏輯公式中定義了公理這一概念。他還定義了推理規則，以根據邏輯公式推導出其他的邏輯公式。希爾伯特把那些源於公理，並通過推理規則接二連三地得到的邏輯公式叫作定理，把那些由被叫作定理的邏輯公式構成的序列叫作形式證明。如果形式系統中的形式證明在某種意義上表示了數學中的證明，那麼就可以說，該形式系統確實摸清了數學的一個方面。如果數學能用形式系統來表示，那麼我們只要研究該形式系統就可以了。
證明相容性——希爾伯特認為，既然建立了用於表示數學的形式系統，該形式系統就需要具備相容性。這裡所說的“相容性”指的是，對於該形式系統的任意邏輯公式 A 都存在以下性質：無法從形式上證明 A 和 
兩者都成立。話說回來，在存在矛盾的形式系統中，所有的邏輯公式都能從形式上證明，所以這一條性質沒什麼意義。如果能夠證明用於表示數學的形式系統具備相容性，那麼就能斷定我們無法從形式上證明 A 和 兩者都成立。
即使證明了相容性，但是一旦有人置疑該證明的有效性，那也不好辦。於是，希爾伯特想到用一個排除了含義的形式系統來明確證明該形式系統自身不存在矛盾。
證明完備性 —— 希爾伯特認為，要想給數學建立一個牢固的基礎，光滿足相容性還不夠。用於表示數學的形式系統不僅要具備相容性，還必須具備完備性。這裡所說的“完備性”，指的是對於該形式系統的任意語句 A，都存在以下性質：能從形式上證明 A 和 至少有一方成立。如果能夠證明用於表示數學的形式系統的完備性，那麼就能斷定我們能從形式上證明 A 和 至少有一方成立。
希爾伯特想通過“導入形式系統”來表示數學，再通過“證明相容性”來表示無法從形式上證明 A 和 兩者都成立，然後通過“證明完備性”來表示能從形式上證明 A 和 至少有一方成立。可以說，他想向我們展示的就是“不存在形式證明的光芒照射不到的黑暗角落”。
這就是通過導入形式系統、證明相容性、證明完備性給數學建立牢固基礎的過程。
那麼，你們理解希爾伯特計劃了嗎？
希爾伯特計劃
導入形式系統
以“形式系統”來表示數學。
即用形式上的符號的序列來表示數學。
證明相容性
證明用於表示數學的形式系統“不存在矛盾”。
即證明對於任意邏輯公式A，都無法從形式上證明 A 和
證明完備性
證明用於表示數學的形式系統是“完備的”。
即證明對於任意語句 A，都能從形式上證明 A 和
10.2.2 猜謎
“米爾嘉大人！”尤里說道，“您剛剛提到的‘形式證明’跟‘證明’這兩個詞……”
“嗯？我吩咐你哥哥說‘讓尤里好好預習’了啊。”米爾嘉說著看向我。
“前一段，我不是跟你詳細說過嗎？尤里……”我說道。
“你只講了形式證明……”尤里支支吾吾道。
“那麼，我們來簡單複習一下。”米爾嘉說道，“在形式系統中，我們把‘邏輯公式’定義為‘符號的序列’，並從邏輯公式中定義一個叫作‘公理’的概念，然後再定義一個根據邏輯公式推導邏輯公式的‘推理規則’。”
她用食指比劃著圈圈，繼續往下講。
“‘形式證明’指的是由邏輯公式構成的一種有限序列 a1, a2, a3, ... , an，它要滿足以下條件。
- a1 是公理。
- a2 是公理，或通過使用推理規則能夠根據 a1 推導出 a2。
- a3 是公理，或通過使用推理規則能夠根據 a1 或 a2（或者 a1 和 a2）推導出 a3。
- ……
- an 是公理，或通過使用推理規則能夠根據之前的任意一個邏輯公式推導出 an。
此時，我們把剛剛這個由邏輯公式構成的序列 a1, a2, a3, ... , an 叫作‘形式證明’，序列末尾的邏輯公式 an 叫作‘定理’。因此‘形式證明’只不過是形式系統中的‘由邏輯公式構成的序列’之一，說的是形式系統之內的事兒，也可以說是屬於‘形式的世界’的概念。”
我們大家都點了點頭。
“而‘非形式證明’是所謂的數學中的證明，說的是形式系統之外的事兒，也可以說是屬於‘含義的世界’的概念。偶爾人們會把形式證明簡稱為證明，這就會引起麻煩。那麼……尤里！”
“在！”尤里“唰”地一下子站了起來。
“我出個謎題來考考你理解了沒。——在形式系統中，能把公理看成是定理嗎？”
“……唔，我不明白。”
“那麼，泰朵拉。”米爾嘉指著泰朵拉。
“我認為……能。”泰朵拉回答道，“定理指的是在形式證明的末尾出現的邏輯公式。例如，假設 a 是公理，然後思考僅由這一個公理構成的邏輯公式的序列 —— 這符合形式證明的條件。出現在該序列的末尾的邏輯公式 —— 雖說它既是第一個也是最後一個 —— 是 a 本身。因此，a 就是定理。所以，任何公理都能說是定理。”
“很好。”米爾嘉說道。
“唔……這樣啊。”尤里嘀咕道。
“下一道題。”米爾嘉緊接著往下講，“假設在完備的形式系統 X 中，語句 a 不是定理。現在，我們往形式系統 X 中追加一個語句 a 作為公理，生成了一個新的形式系統 Y。此時，形式系統 Y 存在矛盾。為什麼？”
……無人應答。
“語句……是什麼來著？”泰朵拉問道。
“不含自由變量的邏輯公式。”米爾嘉馬上回答道。
接著大家又陷入了沉默。
“根據定義來思考吧。‘形式系統是完備的’指的是什麼？”米爾嘉問道。
“對於任意語句 A，都能從形式上證明 A 和 至少有一方成立。”我答道。
“‘語句 a 不是定理’指的是？”米爾嘉又問道。
“就是說無法從形式上證明語句 a 成立。”泰朵拉答道。
“‘形式系統存在矛盾’指的是？”
“能從形式上證明某個邏輯公式 A 和 兩者都成立。”尤里答道。
“那麼，提示已經齊了。形式系統 Y 存在矛盾的原因是？”
回答米爾嘉的仍舊是沉默。
我思考著，不能從形式上證明語句 a，也就是說……
“我明白了！”尤里大喊道。栗色的頭髮一瞬間閃耀著金色的光澤。
“喔……那麼，尤里你說。”米爾嘉指向尤里。
“因為 X 是完備的，所以應該能從形式上證明 a 和 
中的一方成立。”尤里迅速說道，“因為 a 不是定理，所以不能從形式上證明成立。因此， 應該能從形式上證明成立。但是，Y 已經把 a 歸為公理了。這樣一來，就能從形式上證明 a 和 兩者在 Y 裡都成立！所以，形式系統 Y 就存在矛盾了……”
說到這裡，尤里觀察了一下米爾嘉的臉色。
“很好。”米爾嘉說道。
每當梳理邏輯時，尤里都會爆發出驚人的速度……
“就像這樣。”米爾嘉用雙手做了一個捧住大球的手勢，“對完備的形式系統來說，哪怕往公理裡加一個無法從形式上證明的語句，都會出現矛盾。因此比起‘完備’這個詞，用‘完整’更適合 —— 需要的東西都齊全了的意思。”
“完整……”泰朵拉喃喃道。
“我再出一道題。”米爾嘉說道，“如果形式系統存在矛盾，那麼就能從形式上證明該形式系統的所有邏輯公式都成立。現在我們不去證明這個說法，但是一旦認可了這種說法，那麼就會發現存在矛盾的形式系統是完備的。為什麼？”
“啊，的確是這麼回事。”我說道。
“誒？！明明有矛盾還是完備的？”泰朵拉不解。
“泰朵拉，現在你被矛盾和完備這兩個詞的字面含義帶跑了。”我說道，“如果形式系統存在矛盾，那麼就能從形式上證明該形式系統的所有邏輯公式都成立 —— 米爾嘉剛剛是這麼說的，對吧？那麼，由於語句是一種邏輯公式，所以所有語句都能從形式上來證明。這樣一來，該形式系統就是完備的了。因為對完備的形式系統而言，不管選擇何種語句 A，我們都能從形式上證明 A 和 至少有一方成立 —— 這是剛剛已經定義了的，對吧？在矛盾的形式系統中，我們能從形式上證明 A 和 兩者都成立。如果‘能從形式上證明 A 和 兩者都成立’，那麼就能說‘能從形式上證明 A 和 至少有一方成立’，因此存在矛盾的形式系統是完備的。”
米爾嘉點點頭，表示同意我的話，然後說道：
“很好。如果被字面意思帶跑了，那麼一聽到‘存在矛盾的形式系統是完備的’這句話就會覺得很不可思議。然而，從數學上的定義來思考，這一切就理所當然了。”
“存在矛盾就是完備的麼……”泰朵拉嘀咕道。
“我先聲明一下吧。”米爾嘉說道，“我們不能根據‘存在矛盾就是完備的’引申出哲學層面的意義或是人生警句。不，引申不引申是你個人的自由。但是，從數學的角度來說，這種引申是沒有意義的 —— 那麼，我們下面就談談哥德爾吧。”
10.3 哥德爾不完備定理
10.3.1 哥德爾
庫爾特·哥德爾提出的不完備定理的證明發表於 1931 年，那時他 25 歲。論文的題目是《論〈數學原理〉及其相關係統的形式不可判定命題（I）》1。
1原論文英文題為 On formally undecidable propositions of Principia Mathematicaand related systems（I）。論文題目中的《數學原理》一書原書名為 Principia Mathematica，指的是懷德海和羅素所著的書。——譯者注
我來讀一下摘譯的論文開頭部分吧。
一直以來，數學都在朝著追求嚴謹性的方向發展。其結果眾所周知，數學的大部分內容被形式化，甚至可以用幾個機械性的規則來證明。
最全面的形式系統分為兩個方面，一方面是數學原理（Principia Mathematica）系統，另一方面是策梅洛 - 弗蘭克爾（Zermelo-Fraenkel）集合論公理系統。
這兩個系統都很全面。時至今日，我們在數學上使用的所有的證明方法都能夠用這些系統來形式化。也就是說，今天我們在數學上使用的所有證明方法都能夠還原成形式系統中少數的公理和推理規則。因此我們往往會認為：在形式系統中能夠用形式表現的所有數學性問題，都能夠用該系統中的公理和推理規則來判定。
然而這是不正確的，原因如下所示。
哥德爾在這篇論文中證明了數條定理，其中就包括如今被人們稱為“不完備定理”的兩條定理，這兩條定理分別叫作第一不完備定理和第二不完備定理。
哥德爾第一不完備定理
在滿足某個條件的形式系統中，存在滿足以下兩個條件的語句 A。
該形式系統中不存在 A 的形式證明。
該形式系統中不存在
哥德爾第二不完備定理
在滿足某個條件的形式系統中，不存在“表示該形式系統自身相容性的語句”的形式證明。
哥德爾的兩條定理對希爾伯特計劃造成了很大的打擊。這是因為這兩條定理證明了對於滿足某個條件的形式系統而言，我們既不能從形式上證明其“完備性”，也不能從形式上證明其“自身的相容性”。而且，這裡的“某個條件”也非常地自然。
10.3.2 討論
“米爾嘉學姐，我提個問題。”泰朵拉舉起了手，“也就是說，因為‘無法證明數學的相容性’，所以從哥德爾的第二不完備定理可以得出‘數學全都蘊含著矛盾’嘍？”
“錯。剛剛你提出的‘無法證明數學的相容性’，還有‘數學全都蘊含著矛盾’這兩個看法是非常模糊的。我們重新回顧一下第二不完備定理。”
哥德爾第二不完備定理
在滿足某個條件的形式系統中，不存在“表示該形式系統自身相容性的語句”的形式證明。
“哥德爾第二不完備定理不是關於‘數學本身’的定理，充其量只是一個關於‘滿足某個條件的形式系統’的定理。”
“看來不能隨隨便便就把‘數學’和‘形式系統’劃等號啊。”
“而且，”米爾嘉繼續說道，“無法從形式上證明的是‘自身的相容性’。也就是說，滿足某個條件的形式系統無法從形式上證明該系統本身的相容性。但是，在某些情況下還是能夠從形式上證明其他系統的相容性的。”
“雖然不能夠說‘我具備相容性’，但是可以說‘你具備相容性’……是這樣嗎？”泰朵拉問道。
“這說得也有點籠統了，不過，也可以那麼說。就算第二不完備定理存在，也不會妨礙到實際的數學。如果想證明某個系統的相容性，就要使用更強的系統。實際上，數學家們也一直在研究如何證明各種各樣的系統的相容性。如果省略了數學方面的條件，那麼哥德爾不完備定理聽上去就比較過激了。另外，如果忽視‘不完備’這個詞在數學上的含義，而被其字面含義迷惑，那麼推導出的結論就有可能超出數學的範疇。”
“米爾嘉大人，”尤里說道，“我記得有本書裡說‘不完備定理從數學角度證明了理性的界限’……”
“我說尤里，”米爾嘉的眼神變溫柔了，“哥德爾不完備定理是數學定理，數學定理不會去證明什麼理性的界限。”
“是嗎？”
“比如，方程式 x2 = -1 不存在實數解。這表示的並不是理性的界限，由此明確的只是方程式具有的性質。哥德爾不完備定理也是如此，它只是明確了滿足某個條件的形式系統的性質。當然，不完備定理給數學帶來的影響的確很大。但是它帶來的並不是讓數學萎縮的消極影響，而是創造嶄新的數學的積極影響。”
“喔……”
“話說回來，‘理性的界限’這個說法是哥德爾六十歲大壽時奧本海默 2 致的祝辭，並不是帶有數學色彩的主張 3。但是不知道從什麼時候起，這個說法就被人們單獨拿出來用了。”
220 世紀的物理學家，美國籍猶太人，是曼哈頓計劃的主要領導者之一。——譯者注
3出自《哥德爾與 20 世紀的邏輯學 3》（原書名為『 20 世紀論理學 3』，尚無中文版）一書，詳見參考文獻 [30]。
“這麼說來，不完備定理的‘某個條件’是什麼來著？”我問道。
“相容，蘊含皮亞諾算術公理，還要是遞歸的。”米爾嘉說道，“換言之，就是相容、能研究自然數、能夠機械性地判斷邏輯公式的序列是正確的形式證明。雖然哥德爾的論文中使用了比‘相容性’更強的‘ω 相容性’這一條件，但是羅賽爾 4 證明了可以弱化這一條件，只取相容性。”
420 世紀的美國數學家、邏輯學家。——譯者注
10.3.3 證明的概要
“來整體看一下哥德爾證明的大綱吧。這裡把證明分為五個階段，分別把它們叫作春天、夏天、秋天、冬天，還有新春。”
-
春天 —— 形式系統 P
- 定義形式系統 P 的基本符號、公理、推理規則。
-
夏天 —— 哥德爾數
- 把數分配給形式系統 P 的基本符號和序列。
-
秋天 —— 原始遞歸性
- 定義原始遞歸謂詞 5，介紹表現定理（representation theorem）。
-
冬天 —— 探索可證明性的漫漫長路
- 定義算術謂詞乃至可證明性邏輯謂詞。
-
新春 —— 無法判定的命題
-
構成 A 和 都無法證明的命題，也就是不可判定命題。
-
構成 A 和
5原始遞歸謂詞（Primitive Recursive Predicate）是一類數論謂詞。若數論謂詞 P 的特徵函數是一個原始遞歸函數，則稱 P 為原始遞歸謂詞。——譯者注
10.4 春天——形式系統 P
10.4.1 基本符號
在“春天”階段，我們要構建形式系統 P。P 是往數學原理系統中追加了皮亞諾公理和若干條公理後得到的產物。在這個形式系統 P 中，我們可以描述加法運算、乘法運算、冪運算、大小關係，等等。
我們接下來會證明該形式系統 P 中存在無法判定的語句，不過該形式系統 P 只不過是滿足不完備定理成立這一條件的無數系統中的一個而已 ——這一點是毋庸置疑的。
下面我們把數記作 0, 1, 2, .. .，也就是不小於 0 的整數。
首先來定義基本符號。基本符號包括常量和變量。雖然我們不用考慮其含義，但是為了理解起來方便，還是給符號加上一點我們想要的含義吧。
定義常量。
▷常量-1 0 （零）是常量。
▷常量-2 
（後繼數）是常量。
▷常量-3 
（非）是常量。
▷常量-4 
（邏輯或）是常量。
▷常量-5 
（任意的）是常量。
▷常量-6 ( （開括號）是常量。
▷常量-7 ) （閉括號）是常量。
定義變量。變量的類型包括 1, 2, 3, ...。
▷第 1 型變量 x1, y1, z1, ... 是用於數的變量。
我們將其稱為第 1 型變量。
▷第 2 型變量 x2, y2, z2, ... 是用於數的集合的變量。
我們將其稱為第 2 型變量。
▷第 3 型變量 x3, y3, z3, ... 是用於數的集合的集合的變量。
我們將其稱為第 3 型變量。
像上面這樣，一直定義到第 n 型變量。英文字母只有 26 個，所以這裡我們假設可以根據需要使用可數的變量。
10.4.2 數項和符號
定義數項。數項用於在形式系統 P 中表示數。
-
用數項
表示數 0 -
用數項
表示數 1 -
用數項
表示數 2 -
用數項
表示數 3 - ……
-
用數項
表示數 n
▷數項 我們把 
稱作數項。
泰朵拉：“
連成一串，感覺很像音樂符號。”
我：“這裡的 跟皮亞諾公理中出現的撇‘'’的作用相同。”
定義符號。
▷第 1 型符號 我們把 或是 
稱為第 1 型符號，此處設 x 是第 1 型變量。
泰朵拉：“呃……我不太明白。”
米爾嘉：“具體來說，第 1 型符號指的就是 跟 
這樣的。”
▷第 2 型符號 我們把第 2 型變量稱為第 2 型符號。
▷第 3 型符號 我們把第 3 型變量稱為第 3 型符號。
像上面這樣，一直定義到第 n 型符號。
10.4.3 邏輯公式
下面來定義基本邏輯公式。
▷基本邏輯公式 我們把呈 a(b) 這種形式的符號序列稱為基本邏輯公式。
注意，這裡設 a 是第 n + 1 型符號，b 是第 n 型符號。
米爾嘉：“例如像 x2(0)、
和 z3(x2) 這樣的就是基本邏輯公式。”
我：“這……這是集合（元素）的形式麼？”
米爾嘉：“算是吧。”
泰朵拉：“我們想讓 x2(x1) 有 
這個含義？”
米爾嘉：“對。不過類型已經定好了，比如‘x1 是數’‘x2 是其集合’這種。”
定義邏輯公式。
▷邏輯公式-1 基本邏輯公式是邏輯公式。
▷邏輯公式-2 若 a 是邏輯公式，則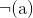 
也是邏輯公式。
▷邏輯公式-3 若 a 和 b 是邏輯公式，則 
也是邏輯公式。
▷邏輯公式-4 若 a 是邏輯公式且 x 為變量，則 
也是邏輯公式。
▷邏輯公式-5 只有滿足以上條件的才是邏輯公式。
泰朵拉：“啊，我明白了。我們定義的是形式系統的邏輯公式呀。”
定義省略形式。
▷省略形式-1 我們將 
定義為 
。
▷省略形式-2 我們將 
定義為 
。
▷省略形式-3 我們將 
定義為 
。
▷省略形式-4 我們將 
定義為 
。
尤里：“定義省略形式是什麼意思？”
我：“就是說為了簡潔，我們要把 寫成 。”
▷括號的省略 為了看起來方便，後面我們會省略冗長的括號。
10.4.4 公理
我們來把皮亞諾公理導入形式系統 P。
▷公理 I-1 
▷公理 I-2 
▷公理 I-3 
泰朵拉：“皮亞諾的公理不是有五條來著嗎？”（2.1.1 節）
米爾嘉：“因為我們之前在使用類型的時候就已經導入了 PA1 和 PA2 啊。”
尤里：“米爾嘉大人，‘=’的定義還沒出來呢！”
米爾嘉：“哥德爾的論文參考了《數學原理》，在論文中他將 x1 = y1 定義成了 
。就是說‘不管集合 u 是什麼樣，只要 x1 屬於集合 u，那麼 y1 就也屬於集合 u’。”
尤里：“嗯？”
米爾嘉：“就是通過‘不存在只包括 x1 或只包括 y1 的集合’定義了‘x1 和 y1 相等’。第 n 型也同理。”
下面我們把命題邏輯的公理導入形式系統 P。
把任意的邏輯公式 p、q、r 代入下面的公理 II-1～公理 II-4 中就能得到公理。
▷公理Ⅱ-1 
▷公理Ⅱ-2 
▷公理Ⅱ-3 
▷公理Ⅱ-4 
下面我們把謂詞邏輯的公理導入形式系統 P。
▷公理Ⅲ-1 
注意，這裡假設：
-
表示“把 a 的所有自由的 6 v 用 c 代換後的邏輯公式”。 - c 跟 v 是同一個型的符號。
- 在 a 裡，v 只要是自由的，c 中就沒有受約束的變量。
6這裡指的是變量、未知數，等等。——譯者注
我：“ 是什麼？”
米爾嘉：“把 a 中的 v 用 c 代換，也就是 substitute 後的結果。我舉例解釋一下吧。”
-
a 是邏輯公式
。 - v 是名為 x1 的第 1 型變量。
-
c 是名為 的第 1 型符號（數項）。
-
此時， 是邏輯公式
。
▷公理Ⅲ-2 
注意，這裡假設 v 是任意變量，b 中不出現自由的 v。
我：“要是 b 裡不出現變量 v，那麼就不會受到 
的影響唄。”
接下來，我們把集合的內涵公理導入形式系統 P。
▷公理Ⅳ 
注意，這裡假設：
- u 是第 n + 1 型變量，v 是第 n 型變量。
- a 中不出現自由的 u。
我：“內涵公理？”
米爾嘉：“對應的是集合的內涵定義。”
我：“什麼意思啊？”
米爾嘉：“總之就是‘邏輯公式 a 能決定集合 u’。”
我們再把集合的外延公理導入形式系統 P。
▷公理Ⅴ 
我們把這個邏輯公式，以及將該邏輯公式“形式提升”後的邏輯公式定為公理。形式提升指的是讓符號的類型都增加相同的數。也就是說，下面這些全都是公理。
-
-
-
- ……
我：“這次是外延公理……”
米爾嘉：“也就是說，假設對於任意 x1，‘x1 是否屬於集合 x2’和‘x1 是否屬於 y2’總是相容的。此時，我們設想集合 x2 跟集合 y2 相等……”
我：“嗯？”
米爾嘉：“這是集合的外延定義。‘集合中的元素決定集合本身’。”
10.4.5 推理規則
我們繼續把推理規則導入形式系統 P。
▷推理規則-1 根據 a 和 
得到 b。
此時，我們稱 b 是根據 a 和 得到的有效結論
。我：“這是假言推理吧。”
▷推理規則-2 根據 a 得到 
。
此時，我們稱 是根據 a 得到的有效結論。
注意，此處的 v 是任意變量。
泰朵拉：“這個是……我不明白。”
米爾嘉：“就是說，既然沒有條件的情況下都能導出 a，那麼即使加上‘任意的’這個條件也能導出 a。”
◎ ◎ ◎
至此，形式系統 P 的定義就結束了。
“春天”結束了。“季節”向著“夏天”——哥德爾數推移。
……在這之前，先吃個午飯吧。
10.5 午飯時間
10.5.1 元數學
我們跟著米爾嘉上到三樓，進了一間寫著 Oxygen 的房間。這個房間佈置得像是一間同時供應零食的咖啡館。天氣很好，於是我們選擇坐在露天陽台的座位上。陽台一邊可以看見海，另一邊則可以看見森林。萬里無雲，陽光柔和。
我點了咖喱飯，尤里要了意大利面，泰朵拉要吃三明治，米爾嘉則點了巧克力撻。
“一牽扯到形式系統，感覺邏輯學就大不一樣了呢。”我說道。
“是嗎？”
“一提到邏輯學，我就只能想到三段論 7 或者德·摩根定律什麼的。從數學角度來研究數學 —— 我沒想到還有這種領域……”
7英文寫作 Syllogism，是邏輯學中由大前提和小前提出發導出結論的一種邏輯推理。——譯者注
“不過這可是數理邏輯學的一部分。”米爾嘉說道。
“為什麼非得把數學形式化呢？”尤里問道。
“要想嚴謹地進行討論，做到形式化是非常重要的。”米爾嘉說道，“例如，假設我們想說‘這個證明是不可能的’，此時就需要定義‘證明是什麼’‘證明是不可能的指的是什麼意思’。沒有這些定義，就沒法區分以下兩者：到底是自己碰巧沒法證明，還是從原理上來講就沒法證明。”
我們大家都對米爾嘉的話點頭表示同意。
“形式化也是對像化，也就是把自己想要討論的東西明確為‘對像’。我們把以數學為對象的數學稱為元數學。意思是‘關於數學的數學’，懂吧？也就是以形式系統來表示數學，再從數學角度去研究‘數學’這個表示結果。”
“這個是……嗯……”泰朵拉說道，“就像是 
語言出現之後，我們才能進一步研究‘極限’，對吧？”
10.5.2 用數學研究數學
“米爾嘉大人，”尤里說道，“關於哥德爾不完備定理，我看到過一本書。書裡說‘人生是不完整的，因而有趣’，還說‘如果全都明白了，人生也就沒意思了’。人家當時有種恍然大悟的感覺，可是……”
“嗯，也有人這麼想。”米爾嘉苦笑，“看到不完備定理的結果，就認為‘因為不明白，所以人生才有趣’。不過，這個吧，簡直就像……”
米爾嘉閉上雙眼，輕輕點了點頭，然後睜開眼。
“就像看到了樣式漂亮的蕾絲圖案就認為‘破了洞也很美’。這些人並沒有理解蕾絲圖案的樣式所衍生的東西。他們只是從表面來觀察這個世界，沒有看穿其結構。這些樣式明明還蘊含著更深的樂趣。數學形式化後，人們就能夠研究數學本身擁有的豐富的數學性結構，可以從數學角度來研究以形式系統表示的數學。這就是‘用數學研究數學’。自己關注的理論有著怎樣的結構，多個理論之間有著怎樣的關係……這明明應該是一個能衍生出非常多樂趣的問題。”
“就是要超越‘伽利略的猶豫’嗎？”我下意識問道。
“不完備不是失敗或者缺點，有可能是通往新世界的入口。”
10.5.3 甦醒
飯後，我從自動販賣機買了瓶水，然後回到了 Chlorine。房間裡一個人也沒有。白板上寫著尤里的留言：
我們去圖書館觀光啦！等我們回來哦
米爾嘉帶她們去參觀圖書館了啊……嘁。
我喝了一口冰涼的礦泉水，開始回顧之前的內容。
嗯，雖然並沒有全部理解，不過大體還算跟得上吧。總之，我們正在構建一個形式系統，下面我記得是哥德爾數跟原始遞歸謂詞的定理來著。最後應該是反證法吧？如果假設存在形式證明，那麼就會發生矛盾……米爾嘉大概會朝這個方向講吧？
不久，飯後睡魔襲來，我趴在桌子上睡著了。
開門聲。
“……所以說，是魚的標記。”泰朵拉的聲音。
“跟密碼似的。”尤里的聲音。
看來女生們回來了。不過我還在半夢半醒之中。
“呀，哥哥睡著了！”
“他一定累壞了。”
“話說回來，你剛剛說的‘態度’是？”米爾嘉的聲音。
“啊，這個……”泰朵拉的聲音。“我一直認為自己學習起來‘雖然花的時間比較長但很有毅力’。可是，光有這點是解不開數學題的，還需要類似靈感的才能，對吧？”
“沒錯，沒錯。”尤里的聲音。
“我有時候想，自己沒法產生靈感，但拓展一下思維應該還是能做到的。所以每逢解題時我就想‘如果換成米爾嘉學姐……’‘如果換成學長……’。”
“喔……”
“我從米爾嘉學姐和學長身上學到了很多好東西，不只是解題方法和訣竅，還有……怎麼說呢，就是類似於‘態度’的東西。應該說是‘樂在其中，並且認真面對’吧。不是光考試考高分就行了，重要的是‘想要去真正理解’的態度。”
“哥哥他呀，一直在研究數學哦。”尤里的聲音。
“學長他，在自己家裡是什麼樣子的？”泰朵拉的聲音。
“這個嘛……哥哥他有點遲鈍呢。”
（喂！尤里！別瞎說呀！）
“而且，明顯有頂撞阿姨的傾向……”
“話說，差不多該叫這只懶貓起床了吧？”米爾嘉的聲音。
（懶貓？）
霎時間，一個冰得夠嗆的玩意兒“咚”地撞到了我的脖子上。
我大聲叫著跳了起來。
“你醒了？”
黑髮才女微笑著，手中拿著我那瓶礦泉水。
“那麼，我們繼續。下面進入‘夏天’。”
10.6 夏天——哥德爾數
10.6.1 基本符號的哥德爾數
在“夏天”階段，我們要談的是哥德爾數。
哥德爾數是分配給形式系統 P 的“符號、符號序列、符號序列的序列”8 的編號。
8有些文獻中也稱“符號、符號串、符號串的序列”。——編者注
首先，我們來定義基本符號的哥德爾數。
我們把不大於 13 的奇數作為哥德爾數分配給常量。
常量
0
(
)
哥德爾數
1
3
5
7
9
11
13
泰朵拉：“為什麼是奇數？”
米爾嘉：“馬上你就明白了。”
把大於 13 的質數分配給第 1 型變量。
第 1 型變量
x1
y1
z1
...
哥德爾數
17
19
23
...
把大於 13 的質數的平方分配給第 2 型變量。
第 2 型變量
x2
y2
z2
...
哥德爾數
172
192
232
...
把大於 13 的質數的立方分配給第 3 型變量。
第 3 型變量
x3
y3
z3
...
哥德爾數
173
193
233
...
像上面這樣，一直到把大於 13 的質數的 n 次方分配給第 n 型變量。這樣一來，我們就把哥德爾數分配給了常量和變量，也就是基本符號。
10.6.2 序列的哥德爾數
我們來定義序列的哥德爾數。注意，這裡的序列指的是有限序列。
因為我們剛才已經定義了基本符號的哥德爾數，所以現在可以用哥德爾數的序列來表示基本符號的序列了。例如，思考下面這樣的哥德爾數的序列。
我們讓這個序列對應下面這樣的乘積。
然後把這個乘積定義為 這個序列的哥德爾數。這裡的 pk 是從小到大排列的第 k 個質數。
例如，表示 2 的數項是 這個基本符號的序列。基本符號 f 的哥德爾數是 3，基本符號 0 的哥德爾數是 1，因此基本符號的序列 可以用下面這樣的哥德爾數的序列來表示。
把這個序列放在質數的指數位置上，構成下面這樣的乘積。
計算該乘積，得到 
。1080 這個數就是基本符號的序列 的哥德爾數。
尤里：“咦？ 不是 2 喵？”
米爾嘉：“含義的世界裡的數 2，在形式的世界裡是用數項 來表示的。”
尤里：“瞭解。”
米爾嘉：“把 這個符號序列用哥德爾數表示就是 1080。”
尤里：“喔……”
米爾嘉：“泰朵拉，你想沒想到為什麼要在基本符號這裡用奇數？”
泰朵拉：“這……我不知道。”
米爾嘉：“我們可以通過哥德爾數的奇偶來判斷哥德爾數是否構成序列。”
泰朵拉：“哦哦，如果哥德爾數是偶數，就表示序列！”
剛才我們給出了基本符號的序列 的示例。符號序列的哥德爾數跟符號序列的序列的哥德爾數可以用同樣的思路來考慮。也就是說，不管構成序列的是什麼東西，我們只要把構成序列的那個東西的哥德爾數放到按升序排列的質數的指數部分，取它們的乘積即可。
多虧質因數分解的唯一性，我們才能根據哥德爾數還原出唯一的序列。哥德爾的論文中用的是我們剛才說明的方法 —— 質數指數記數法，不過換成其他方法也可以。
那麼，因為邏輯公式是符號序列，所以我們就可以定義“邏輯公式的哥德爾數”了。又因為形式證明是邏輯公式的序列，也就是符號序列的序列，所以我們還可以定義“形式證明的哥德爾數”。
這樣一來，我們就可以把形式系統的一切都用哥德爾數這個數來表示了。
泰朵拉：“關於序列是符號序列還是符號序列的序列，能用哥德爾數來區分嗎？”
米爾嘉：“這道謎題就留給你來解答吧。”
泰朵拉：“誒？兩者都要是偶數，對吧？”
我：“我明白了。”
米爾嘉：“閉嘴。”
泰朵拉：“……我明白了。要看把哥德爾數質因數分解的時候出現的 2 的個數。”
米爾嘉：“2 的個數怎麼了？”
泰朵拉：“如果 2 的個數是奇數，就是符號序列；如果是偶數就是符號序列的序列。”
米爾嘉：“很好。”
對於不完備定理，我們關注的是“形式證明是否存在於形式系統之中”。但是，如果不是“能理解形式證明的形式系統”，這樣的問題就沒有意義了。哥德爾用哥德爾數把形式證明譯成了編碼。這樣一來，只要一個形式系統“能理解數”，那麼這個形式系統就能理解形式證明。
泰朵拉：“把一切都用哥德爾數來表示……這個想法跟計算機的思路 —— 把一切都用位來表示很像呀。”
米爾嘉：“泰朵拉，你說反了。世界第一台計算機誕生於 1940 年代，哥德爾的證明在那之前喲。”
那麼，到這裡“夏天”就結束了。我們進入“秋天”吧。
10.7 秋天——原始遞歸性
10.7.1 原始遞歸函數
在“秋天”階段，我們需要先離開一下形式系統 P，去一趟含義的世界。
接下來，我們要定義一個函數的同伴 —— 原始遞歸函數。這個函數用一句話說就是：獲取函數的值時需要的“重複次數”存在上限的函數。
例如，求 n 的階乘 
的函數 
就是一種原始遞歸函數，我們可以像下面這樣來定義它。
下面試著求一下 
吧。
像這樣，要計算 ，只要使用 4 次定義即可；要計算 ，只要使用 n + 1 次定義即可。這就是“重複次數有上限”的含義。
事實上，要想計算 的值，還需要用到“×”和“+”的運算，所以我們再說得詳細點兒吧。
假設函數 F, G, H 是用於處理數 (0, 1, 2, .. .) 的函數。
如下定義函數 F 時，我們稱函數 F 是由函數 G 和 H 經原始遞歸定義 9的。