微積分的歷程：從牛頓到勒貝格：第12章沃爾泰拉_William Dunham

維托·沃爾泰拉（1860—1940）

在19世紀後半葉意大利出現的一批並駕齊驅的數學家中，維托·沃爾泰拉是久負盛名的佼佼者。同他的同胞朱佩塞·佩亞諾（1858—1932）、猶金尼奧·貝爾特拉米（1835—1900）和尤里斯·迪尼（1845—1918）一樣，由於在像靜電學和流體力學這樣的應用科學領域以及像數學分析這樣的理論研究領域作出了貢獻，他在科學史上留下不可磨滅的痕跡。自然，我們在這裡要考察的是他的後面一種貢獻。

雖然沃爾泰拉出生在亞德裡亞海之濱，但是他是在意大利中部的佛羅倫薩長大的，這座城市是意大利文藝復興運動的發祥地。在佛羅倫薩，沃爾泰拉徜徉於偉大藝術家米開朗琪羅漫步過的街道，就讀於以詩人但丁和科學家伽利略命名的學校。15世紀和16世紀佛羅倫薩文藝復興時代的氣息彷彿滲入了他的骨髓，因為沃爾泰拉酷愛藝術、文學和音樂，正如他熱愛科學一樣。他儼然是一位博學多才的文藝復興式的人物，雖然那場開始於佛羅倫薩的運動已經過去了三個世紀。

除這些事業外，他的政治勇氣也是值得稱讚的。沃爾泰拉目睹了法西斯頭目墨索里尼在20世紀20年代的發跡和上台，他站在公開反對的立場，並在一份抵抗這個政權的聲明上簽名。這個舉動最終使他丟掉了工作，然而這讓他成為意大利那個時代知識界中的一位英雄。直到1940年他去世時，意大利尚未擺脫法西斯統治的災難，但是沃爾泰拉已經為預期中的美好前景進行了奮勇戰鬥。

如果說晚年時代的沃爾泰拉展現出了巨大勇氣，那麼少年時代的他則顯示了絕頂的聰慧。年幼的沃爾泰拉早在11歲時就閱讀了大學水平的數學教科書，給他青春時期的教師們留下深刻的印象，並且還在高中時已通過某種途徑在佛羅倫薩大學謀求得物理學實驗助理的職位。他在學術上的發展突飛猛進，並在22歲時所寫的物理學博士論文中達到頂峰。1

1 這段傳略是根據Dictionary of Scientific Biography（《科學家傳記詞典》）vol. XIV, pp. 85-87的「沃爾泰拉」條目編寫的。

在這一章我們要討論沃爾泰拉的兩項早期發現，兩者都是在1881年發表的，這是他在高中畢業三年之後。第一項發現是找到一個病態函數，在不斷增加的病態函數反例表中又增添了一個新的實例，並且從這個例子找到黎曼積分中以往從未引起人們注意的一個漏洞。第二項發現看似矛盾而實際是正確的，就是獲得對於病態函數具有其自身限度的證明，因為沃爾泰拉證明了這樣一個定理：不可能存在在每個有理數點連續而在每個無理數點不連續的函數。這樣一種函數由於過度病態而無法存在。我們將要全面考查這個定理，不過先從那個病態函數的反例的簡要說明開始。

沃爾泰拉病態函數

我們在第6章曾見過微積分基本定理的第二種形式，由柯西陳述如下：

「如果函數F是可微的，並且它的導數F'是連續的，那麼。」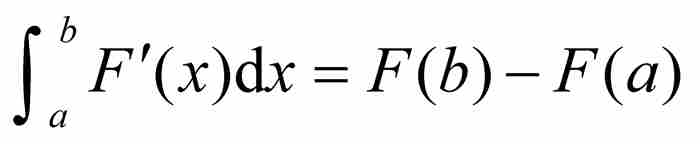

不嚴格地說，這表明在正確條件下導數的積分恢復其原函數。柯西在定理的證明中利用了兩個假設：（a）函數F存在導數，（b）這個導數自身是連續的。但是，這兩個假設是必要的嗎？

假設（a）似乎是不可或缺的，因為我們不能指望在導數不存在的情形下對一個導數進行積分。然而，假設（b）的必要性就值得懷疑了。為了使基本定理成立，難道我們必須作出像F?的連續性這樣嚴格的限制嗎？

這並不是一個無足輕重的問題。我們在第10章曾見過，不能把導數的連續性視為理所當然的事情，因為函數

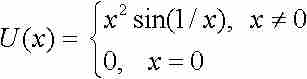
就有一個不連續的導數。另一方面，我們無需用導數的連續性作為一個積分存在的保證，因為很容易找到導數不連續然而卻是可積的函數。

於是，問題在於，如果說存在任何條件的話，那麼我們應該對導數F'加上什麼條件方能保證基本定理成立。過去的種種發現為數學家們提供一種看待這個問題的視角，而這是柯西不曾有過的，所以看來值得重新討論這個重要的定理。

在1875年，伽斯騰 · 達布成功地削弱了假定（b）。他證明，只要（a）函數F是可微的，以及（b'）它的導數F'是黎曼可積的，就有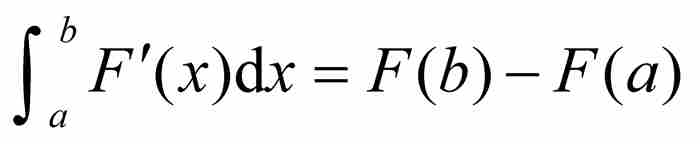。因此，為了保證基本定理成立，我們不再需要假定F'的連續性，只要求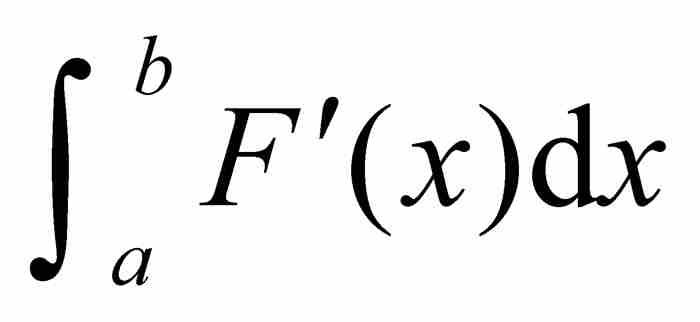存在就足夠了。

這已經算是一種進展，但是依然存在一個關於F'的問題，即我們是否需要對它作出不同於存在性的其他任何假設。或許導數是可積的原系它們固有的特定性質。要是如此，我們就可以同時拋棄假定（b）和（b'），並且單獨在假定（a）的基礎上建立微積分的基本定理。那樣將是一種限制更少和更顯優雅的情況。

這就特化成這樣一個問題：可能允許導數帶有何等不良特性？在第10章我們證明了達布定理，那裡縱然不要求導數是連續的，但是它必須具備介值特性。在那一點上，導數似乎是完全「順從的」，而數學家們可能猜測這樣的順從性將包含可積性。

年輕的沃爾泰拉在他1881年發表的論文「論積分學原理」2中駁斥的正是這個錯誤概念。在那篇論文中他提供了一個函數F的例子，F在所有點具有有界的導數，但是它的導數是極端不連續的，以致是不可積的。換句話說，儘管F是處處可微的，而且它的導數F'也是有界的，然而積分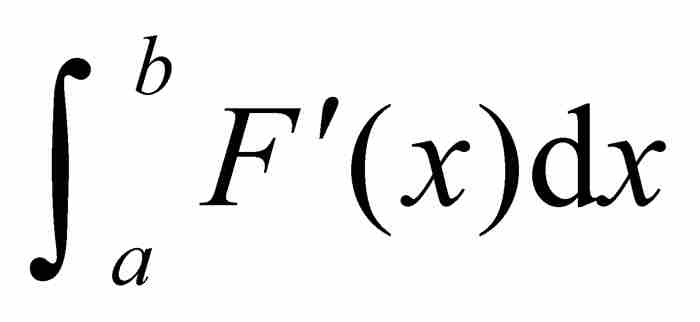並不存在。正是由於這個原因，等式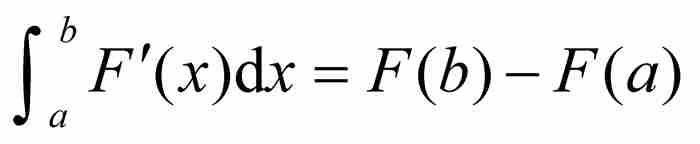不再成立。沃爾泰拉的例子之所以引人注目，不是因為這個式子的左端同右端不等，而是因為左端的積分是沒有意義的。

1 Vito Volterra, Opere Mathematiche, vol.1, Accademia Nazionale dei Lincei, 1954, pp. 16-48。

對於他的病態函數例子我們不作仔細考察，一部分原因在於這個函數很複雜，而另一部分原因是只在一章中討論一個病態函數（魏爾斯特拉斯病態函數）或許就足夠了。有興趣的讀者從文獻3中會找到對於沃爾泰拉的工作的討論。

2 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, pp. 56-57。

有一件事是明確的：黎曼積分的另一個不祥特徵已經被揭露。數學家們喜歡的無非是一個簡潔的定理，大意是如果F是可微的，並且具有有界的導數F'，那麼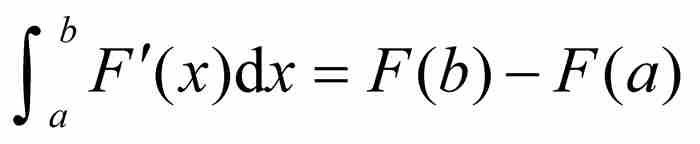。但是，沃爾泰拉證明了，就黎曼積分而論這個定理是不成立的。

對於沃爾泰拉的奇特例子，數學家們可以作出何種反應？一種選擇是接受這個結果，然後繼續前進。當應用這個定理時，簡單地附加一個關於導數F'的額外假設。這將是阻力最小的途徑。

不過，還有另外一種選擇。正如我們先前所見，黎曼積分不能保證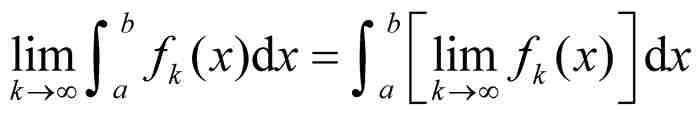。如今，沃爾泰拉已經使建立一個簡單的微積分基本定理的任何希望化為泡影。在19世紀臨近終結之際，有著比以往更多的理由懷疑，麻煩隱藏在黎曼積分的定義中而不在分析學的固有本性中。少數大膽的人，為了挽救上述基本定理，在沃爾泰拉病態函數的推動下打算放棄黎曼積分。不過我不再繼續討論。

漢克爾的函數分類

截至19世紀80年代，分析學受到病態函數反例的巨大衝擊，這些反例看起來一個比一個奇特。我們已經見過的反例包括以下三個。

（a）狄利克雷函數

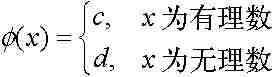
它是處處不連續的但不是黎曼可積的函數。

（b）擴充的直尺函數R(x)，它是在每個無理數點連續而在每個有理數點不連續的函數，但是它是黎曼可積的，其積分。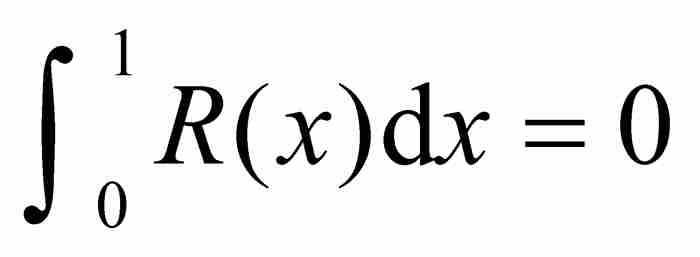

（c）魏爾斯特拉斯病態函數

它是處處連續的和無處可微的函數。

這種情景顯示分析學中存在的混亂局面，而且喚起對於如此雜亂無章的數學現狀確立秩序和條理性。

竭力完成這個重任的人正好是赫爾曼·漢克爾（1839—1873）。他是黎曼的仰慕者，黎曼相信應該像生物學家或者地質學家那樣，採用某種類似的方法對函數進行分類。漢克爾於1870年（早逝之前三年）提出了這樣一種分類。他希望用這種分類闡明數學分析的性質和限度。

漢克爾考察由定義在一個區間[a, b]上的所有有界函數構成的函數族，並且通過它們的連續性和不連續性的性質對它們加以區分。為了瞭解他是如何進行分類的，我們回顧格奧爾格·康托爾曾經給出的一個熟悉的定義。

定義　對於一個實數集A，如果在任何開區間中至少包含A的一個元素，就說A是稠密的。

稠密集的兩個基本例子是有理數集和無理數集，因為任何一個開區間都含有無限多有理數和無理數。稠密集這個名稱帶有啟示性，表明它的元素如此緊密地聚集在一起，以致它們總是毗連的。

有了這個準備，我們就可以對函數給出漢克爾的分類。他把在區間[a, b]上的所有點連續的函數列為第1類函數。這些函數具備很好的特性，它們在區間上達到極大值和極小值，具有介值特性，並且能夠積分。在漢克爾的分類中，第1類函數處於「食物鏈」的頂端。

他的第2類函數包括那些在[a, b]上除有限個點之外是連續的函數。這類函數帶有更多的不確定性，但是它們的奇異性在數量上是有限的，在很大程度上處於控制之中。一個例子是我們在第10章見過的定義在區間[-1, 1]上的函數

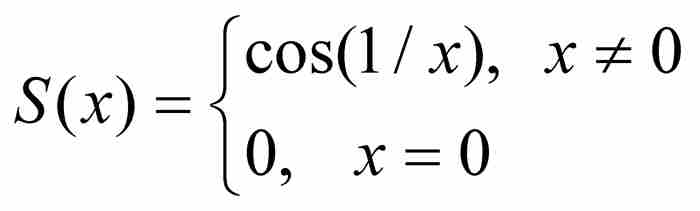
因為它在x = 0有一個不連續點。換一種方法，我們還可以取一個在區間[a, b]上定義的連續函數，然後，例如在50個點上把它重新定義成不連續的，由此引入50個不連續性點。這樣一個函數將屬於漢克爾第2類函數。

從邏輯上說，只剩下一類函數了，即那些在[a, b]上具有無限個不連續點的函數。自然，這些函數是最差的，但是漢克爾相信可以把它們再分成差的和非常差的兩類：

3A類：在[a, b]的無窮個點不連續但是仍然在其中一個稠密集上連續的函數。他把這類函數稱為「點態不連續的函數」。
3B類：一切其他的不連續函數。漢克爾稱之為「完全不連續的函數」。

我們看出，3A類函數中的一個點態不連續函數，儘管存在無限多個不連續點，但是仍然在任何開區間的某些地方是連續的。另一方面，對於3B類中的一個函數而言，必定存在區間（a, b）內的某個開子區間（c, d），函數在其中完全沒有連續的點。因此，一個完全不連續的函數的特徵是在一個不間斷的子區間上僅存在不連續的點。

試問，前面引入的三個病態函數屬於漢克爾分類方案中的哪一類？狄利克雷函數是處處不連續的函數，屬於完全不連續的3B類函數。直尺函數在無窮個點（有理數點）是不連續的，然而在一個稠密集（無理數點）上是連續的，因此屬於點態不連續的3A類函數。魏爾斯特拉斯函數或許是最為奇特的，把它歸入第1類函數看似不當而實則正確的，因為它是處處連續的。

漢克爾發現，他的函數分類在下述意義下是重要的：他知道了第1類函數和第2類函數是黎曼可積的，並且他瞭如指掌的那些點態不連續函數的例子同樣是可積的。相反，完全不連續的狄利克雷函數是不可積的。對於他而言，3A類函數同3B類函數之間的鴻溝似乎是不可跨越的。正如Thomas Hawkins指出的那樣，「漢克爾通過確定點態不連續函數同完全不連續函數之間的區別，相信自己已經把數學分析可以處理的函數同那些它無力處理的函數分離開來」。1

1 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, p. 30。

為了顯示這樣做的全部價值，漢克爾證明了一個驚人的定理：區間[a, b]上的一個有界函數是黎曼可積的，當且僅當它不比點態不連續函數更差。這就是說，一個有界函數只要屬於第1類、第2類或者3A類函數，那麼它是可以積分的；那些屬於3B類的函數是不可以積分的，而且也不能進行解析開拓。

漢克爾定理看起來是在回答我們前面提出的主要問題：一個可積函數可能在多大程度上是不連續的？按照他的說法，答案是「在最壞的情況下是點態不連續的」。他的證明表示，只要一個函數在一個稠密集上是連續的，所有那些不連續的點對於可積性而言都是無足輕重的。這恰好是數學家們夢寐以求的簡潔結果。

不幸的是，這也是不正確的。

在這種錯綜複雜的概念中，即使大學問家也難免犯錯誤，不過漢克爾所犯的是一個突出的錯誤。公正地說，他的定理有一半是正確的：一個函數如果是黎曼可積的，那麼它確實必定在一個稠密集合上是連續的。一個完全不連續的函數存在一個由不連續點構成的不間斷的子區間，它不可能具有黎曼積分。關於這一點，人們再次想到狄利克雷函數。

但是，漢克爾對於相反結論的證明存在漏洞。英國數學家亨利·約翰·斯蒂芬·史密斯（1826—1883）發表了一個點態不連續的函數的例子，而這個函數卻是不可積的。他指出：「這個函數是值得注意的，因為它同一種不連續函數的理論對立，而這種理論得到卓越的幾何學家赫爾曼 · 漢克爾博士的首肯，他在不久前英年早逝是數學科學的巨大損失。」 2 史密斯的例子是非同尋常的，其中用到一種我們如今稱為具有正測度的無處稠密集的結構。需要瞭解細節的讀者，請參閱Thomas Hawkins的著作。3 暫時，我們僅限於指出，函數的連續性同黎曼可積性之間的關係依然是不清楚的，仍舊沒有解決一個可積函數可能在多大程度上是不連續的問題。無論點態不連續性的價值怎樣，它都不能對於人們長期以來尋找的這種聯繫提供答案。

2 H. J. S. Smith, 「On the Integration of Discontinuous Functions」, Proceedings of the London Mathematical Society, vol. 6 (1875), p. 149。

3 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, pp. 37-40。

不過，已經取得了一定進展。黎曼已經把可積性概念擴展到某些高度不連續的函數，而漢克爾定理正確的一半以及史密斯的函數反例，證明了黎曼可積函數完全包容在一個更大的函數集合內，即由在稠密集上的連續函數組成的集合。

我們順便指出，「點態不連續的」這個術語有時被粗心大意地用來表示「在最壞的情況下是點態不連續的」。就是說，凡是屬於漢克爾的第1類、第2類或3A類中的所有函數都被歸並在點態不連續函數這個單一的標題下，這就導致把連續函數（第1類函數）置於「點態不連續函數」之列這種離奇的局面。由於前面三類函數的一個共同特性是在稠密集上是連續的，我們可以把稠密地連續的看成是概括第1類、第2類和3A類中所有函數的術語。

無論如何，初看起來漢克爾的函數分類似乎是一個大有可為的工具，能夠把分析學可以處理的函數同分析學難以對付的函數分離開來。然而，結果卻是許多難以對付的函數在集合論和勒貝格積分的範圍內得到非常巧妙的處理。如今，漢克爾的函數分類多半被束之高閣。

但是在19世紀後期，點態不連續性仍然是最出色的數學家們研究的對象。21歲的維托·沃爾泰拉就是這些數學家中的一位。

病態函數的限度

病態函數的盛行顯示，函數的任何特性，無論它多麼稀奇古怪，通過一位極富創造性的數學家精心構造出的例子，都是可以被認識的。

例如，誰能想像直尺函數竟然會在每個無理數點連續而在每個有理數點不連續呢？此外，為什麼不假定在某處存在一個有待發現的同樣離奇的函數，這個函數在每個有理數點連續而在每個無理數點不連續？似乎並不是一個例子比另外一個例子更加怪異。

從下面的兩個例子中，明顯看出函數的連續性點同不連續性點有時是可以交換的。首先定義函數

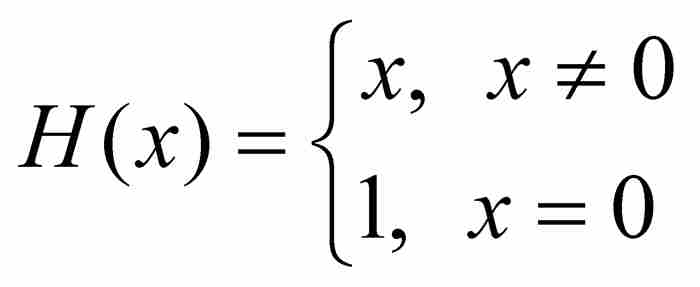
顯然這是在除原點以外的所有點連續的函數，原點是其唯一的不連續點。

作為H(x)的相似函數，我們引入

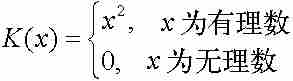
不難看出，K(x)在任何點a = 0是不連續的。因為如果令{x_k}是一個收斂於a的有理數序列，而{y_k}是一個收斂於a的無理數序列，那麼

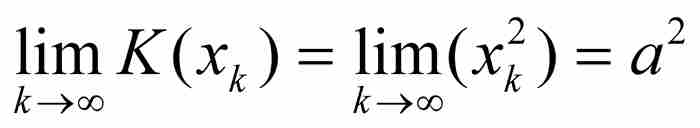
然而

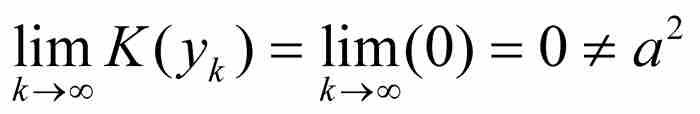
由於這兩個序列具有不同的極限，我們知道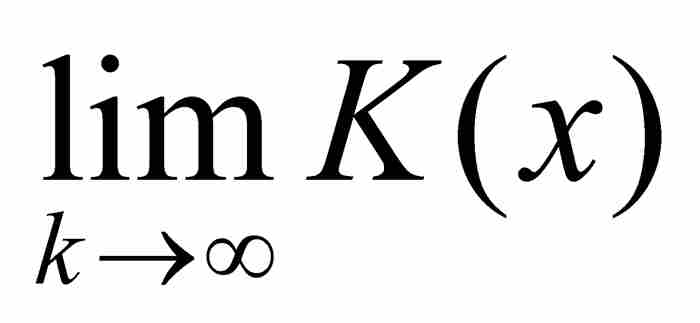不可能存在，所以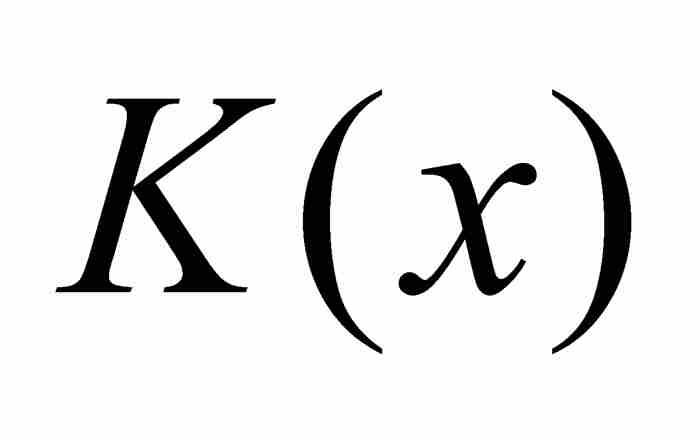在x = a是不連續的。

但是，對於任何x，不管它是有理數還是無理數，我們都有 0≤K(x)≤x2，所以用簡單的擠壓論證，證明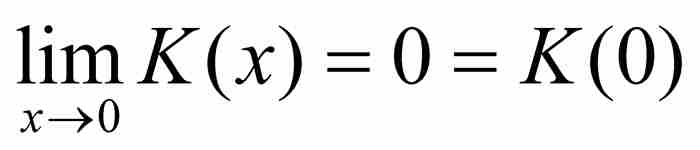。由此推出K有唯一的連續點，即原點。所以，對於上面定義的兩個函數H和K，它們連續的點同不連續的點是相互交換的。

關於這一點，我們引進下面的定義。

定義　地對於一個函數f，我們令C_f = {x| f 在x是連續的}，D_f = {x| f 在x是不連續的}。

可以把前面的討論簡單地概括為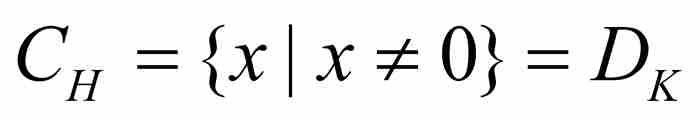和。

函數的連續性點同不連續性點的交換問題是非常有趣的。對於任何一個函數 f，是否存在一個「余函數」g滿足C_f = D_g和C_g = D_f ？要是存在，我們如何把它找出來？倘若不存在，原因又在哪裡？

沃爾泰拉在他1881年所寫的論文「關於點態不連續函數的幾點注記」中致力於解決這個問題。結果得到一個強有力的定理和兩個重要推論。1

1 Vito Volterra, Opere Mathematiche, vol.1, Accademia Nazionale dei Lincei, 1954, p. 7-8。

定理　在區間（a, b）上不可能同時存在兩個點態不連續函數，其中一個函數的連續性點是另一個函數的不連續性點，反之亦然。

證明　他通過反證法證明，首先假定f和φ是（a, b）上這樣兩個點態不連續的函數，它們的連續性點集和不連續性點集滿足C_f = D_φ 和D_f = C_φ 。換句話說，C_f 和C_φ 把（a, b）劃分成兩個不相交的非空稠密子集。

他的證明基於一個嵌套的子區間序列。由於f是點態不連續的，它在區間（a, b）內的某處必定有一個連續的點x_{0。對於ε = 1/2，連續性保證存在一個δ > 0，使（x_{0 - δ , x_{0 + δ ）成為（a, b）的一個子集，並且只要0 < | x - x_{0 | < δ，就有| f (x) - f (x_{0)| < 1/2。現在我們選擇a_{1 < b_{1，使得[a_{1, b_{1]是開集（x_{0 - δ, x_{0 + δ ）的一個閉子區間，如像圖12-1中畫出的那樣。}}}}}}}}}}}

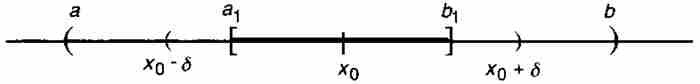
圖　12-1

對於[a_{1, b_{1]中的任意兩點x和y，應用三角不等式，得到}}

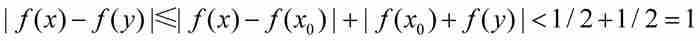（1）

這表明f在閉區間[a_{1, b_{1]上的振幅不超過1單位。}}

但是（a_{1, b_{1）是（a, b）的一個開子區間，同時 φ 也是點態不連續的。因此，（a_{1, b_{1）內有φ 的一個連續點，比如說x_{1。重複前面對於 φ 的論證，我們找到點，使閉區間[, 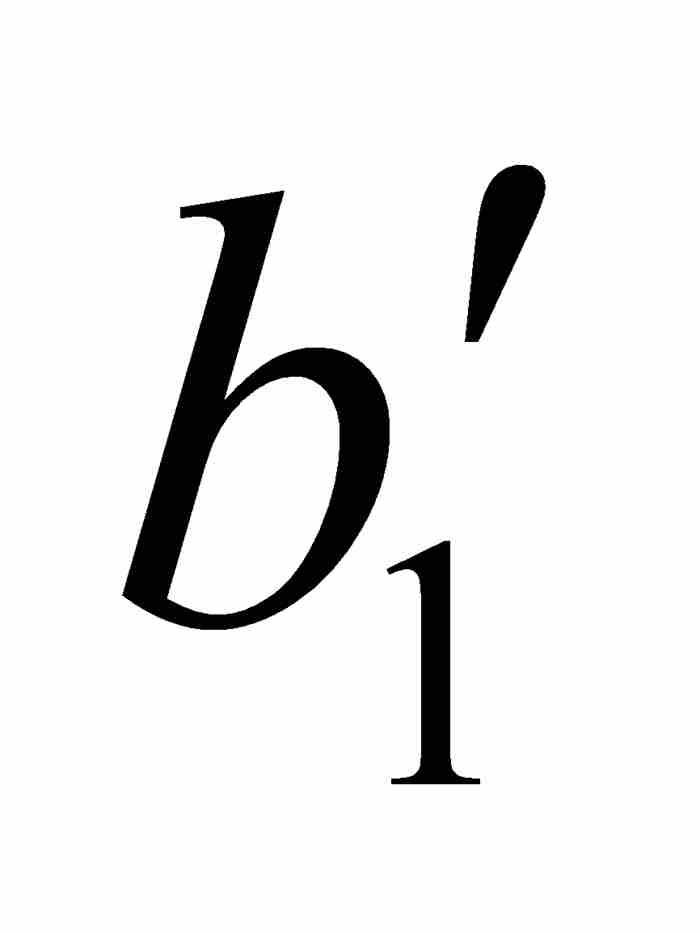]是（a_{1, b_{1）的子集，並且對於[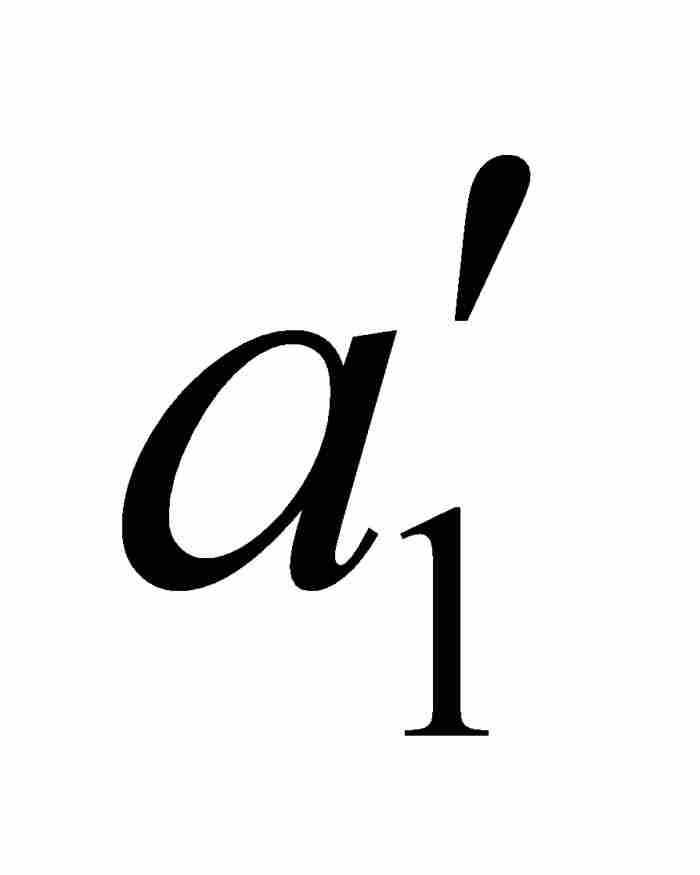, 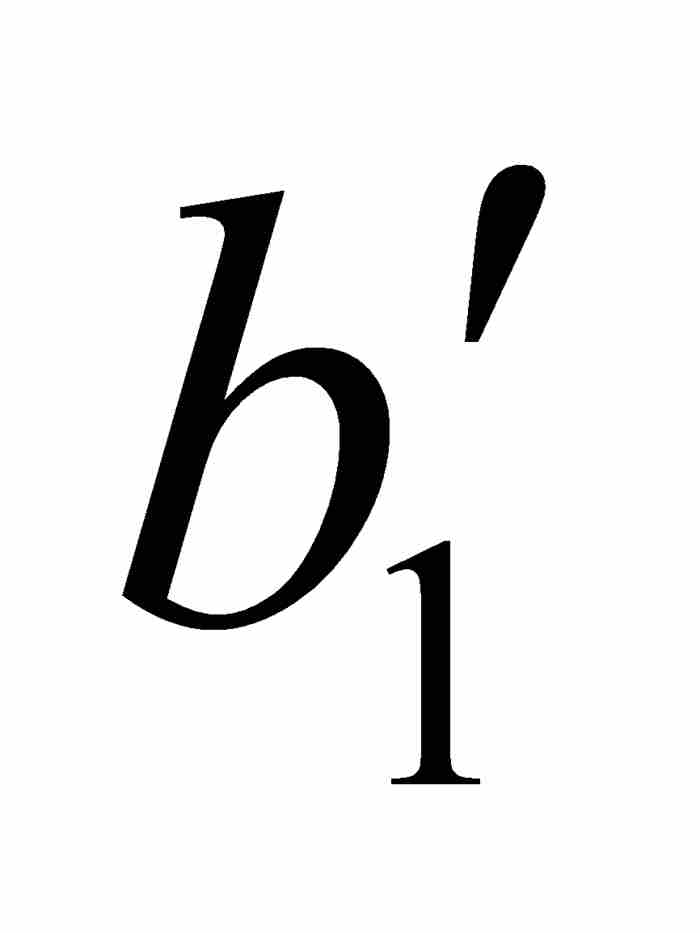]中的任意x和y有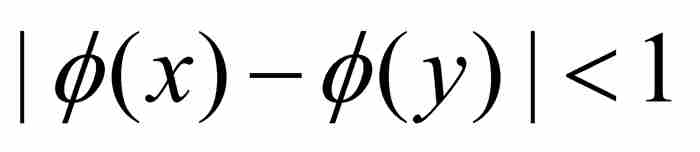。參見圖12-2。}}}}}}}

圖　12-2

把這個結論同上面的式（1）相結合，我們找到一個閉子區間[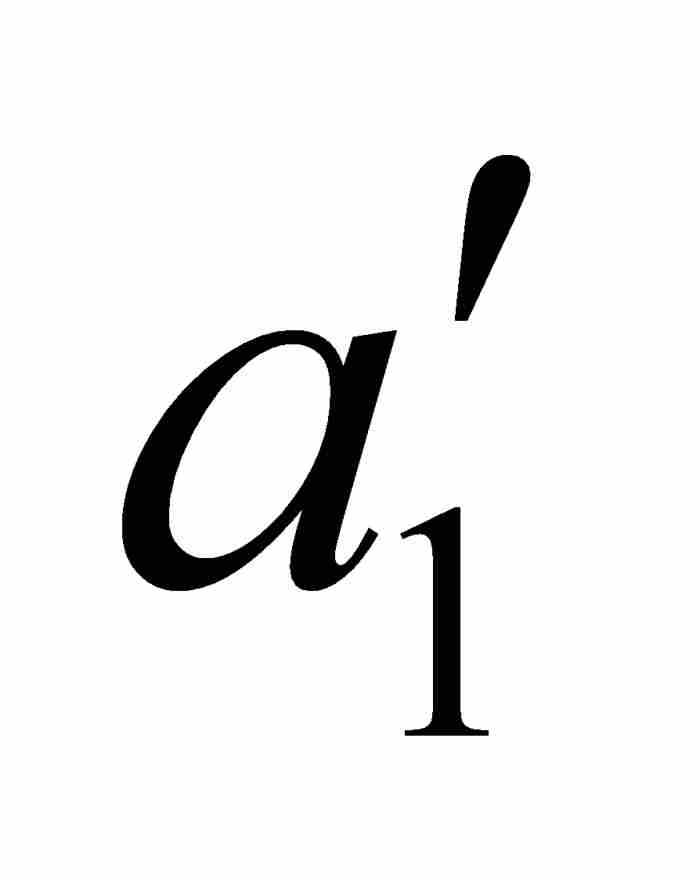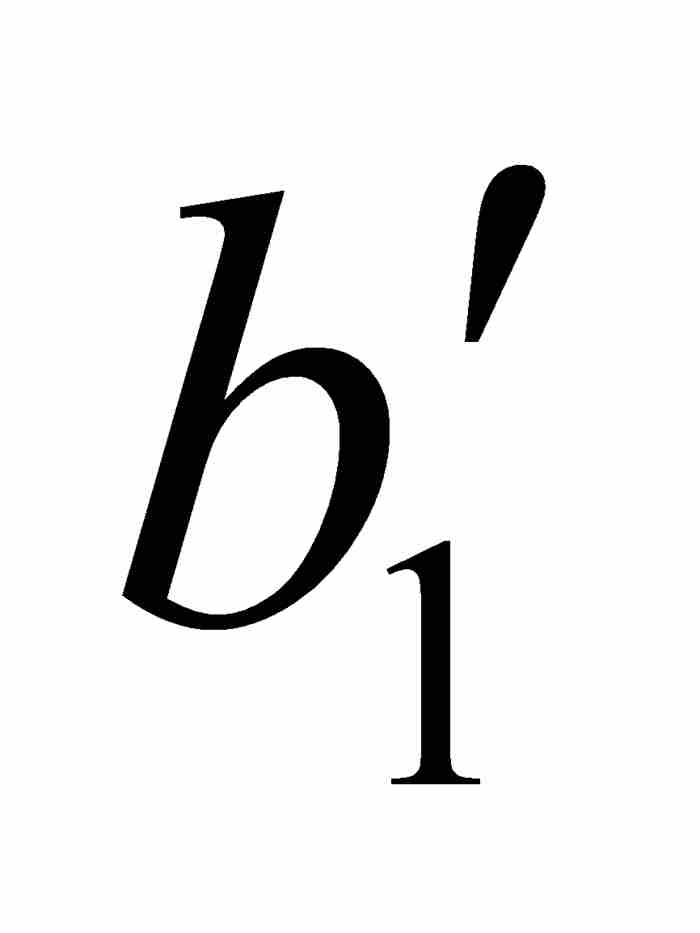，]，對於其中的所有x和y，有

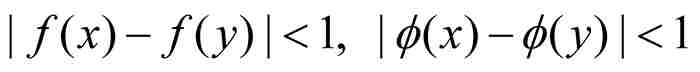
沃爾泰拉接著利用點態不連續性以 ε = 1/4重複這個論證過程。他首先考察f，然後考察 φ，找到一個位於開區間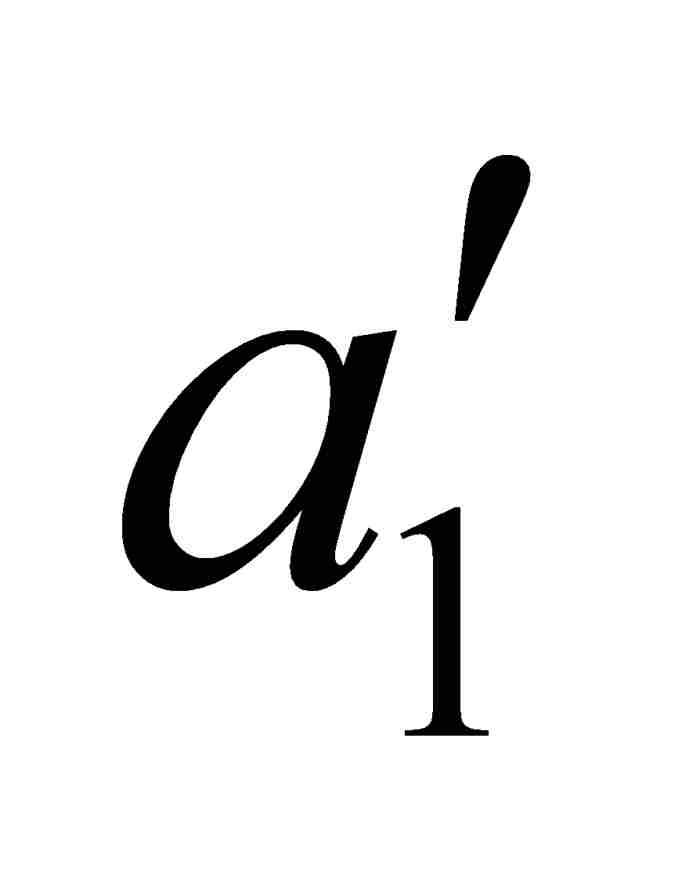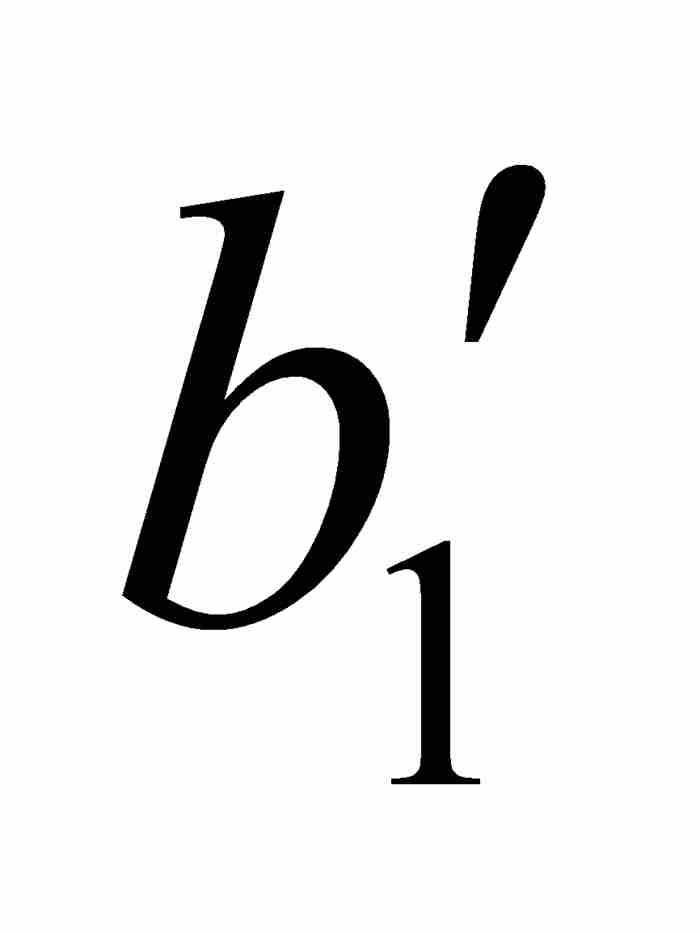（, ）內的閉子區間[, 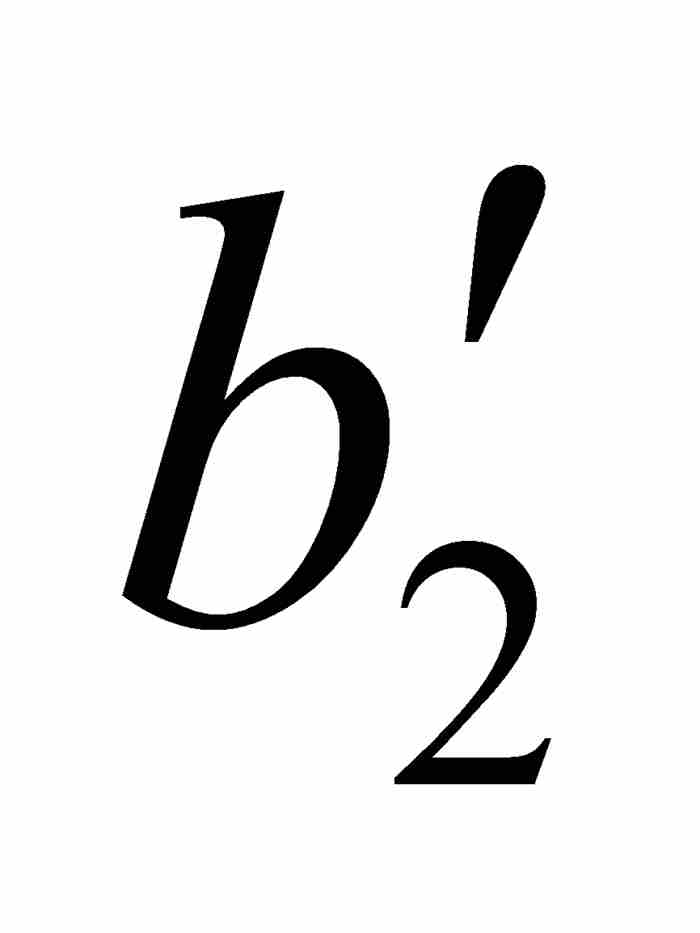]——這個閉區間自然也在[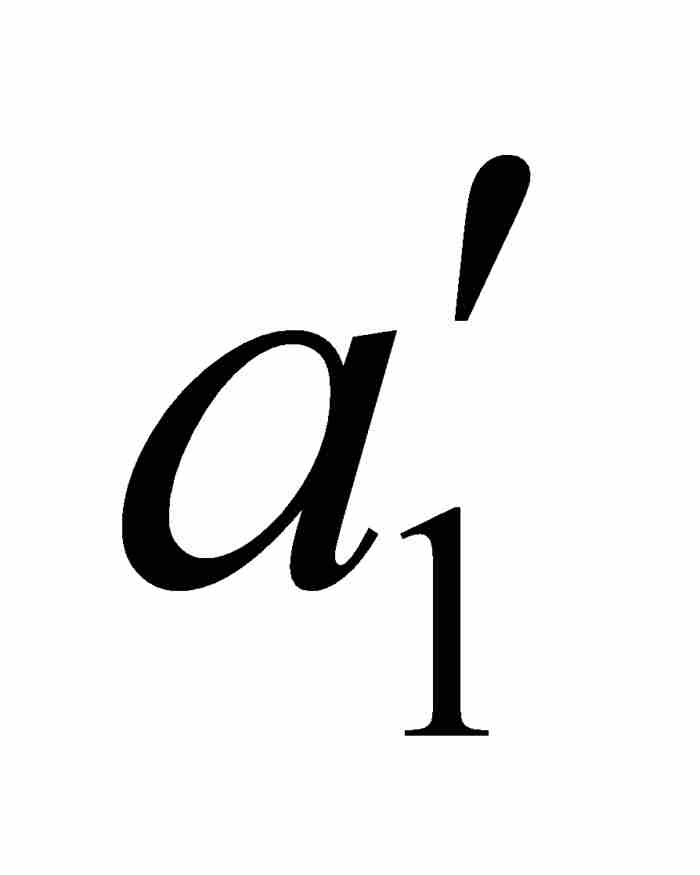, 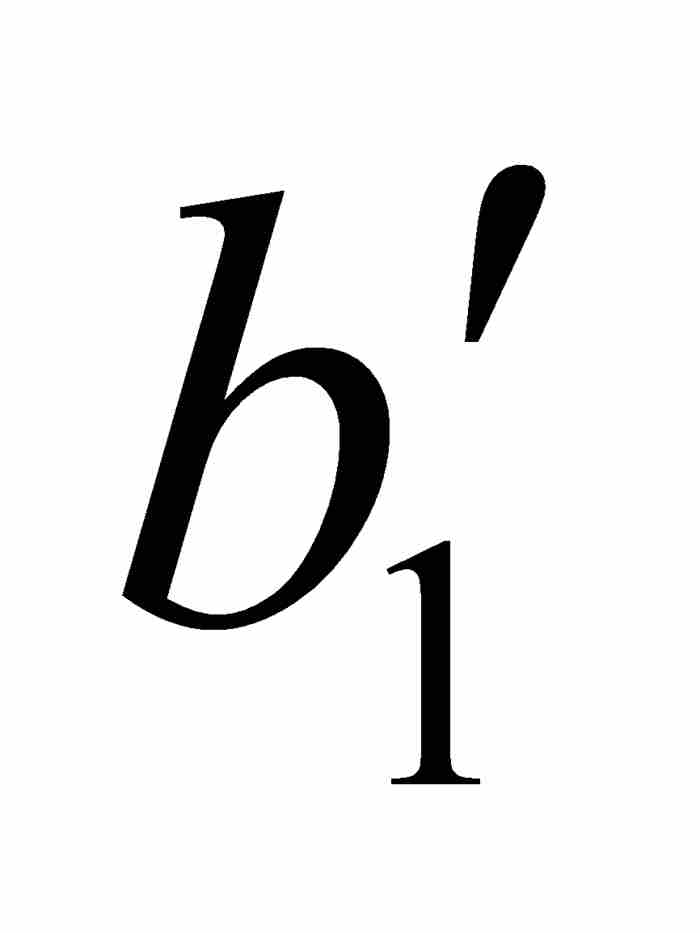]內，使得對於[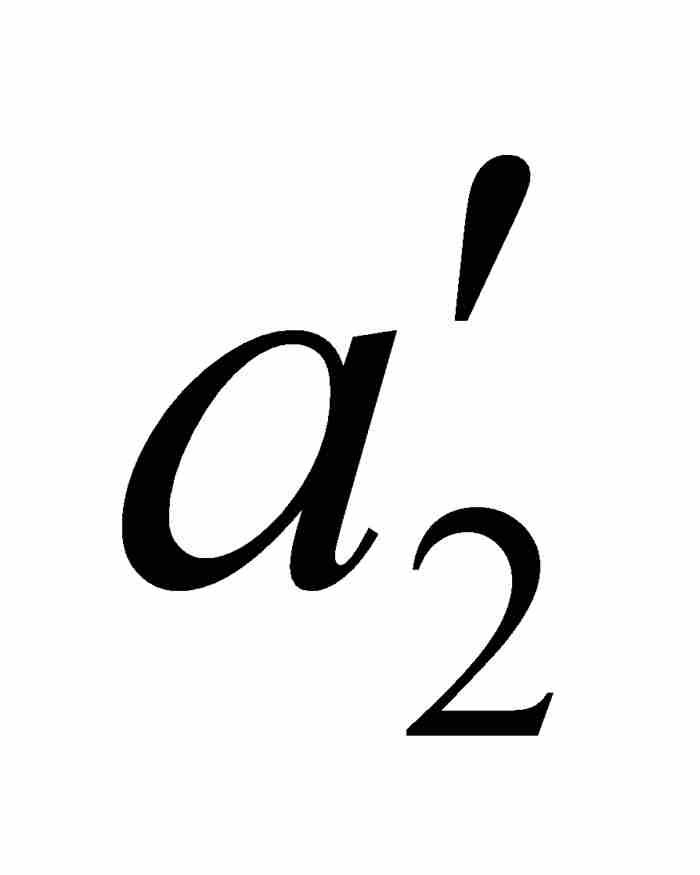, 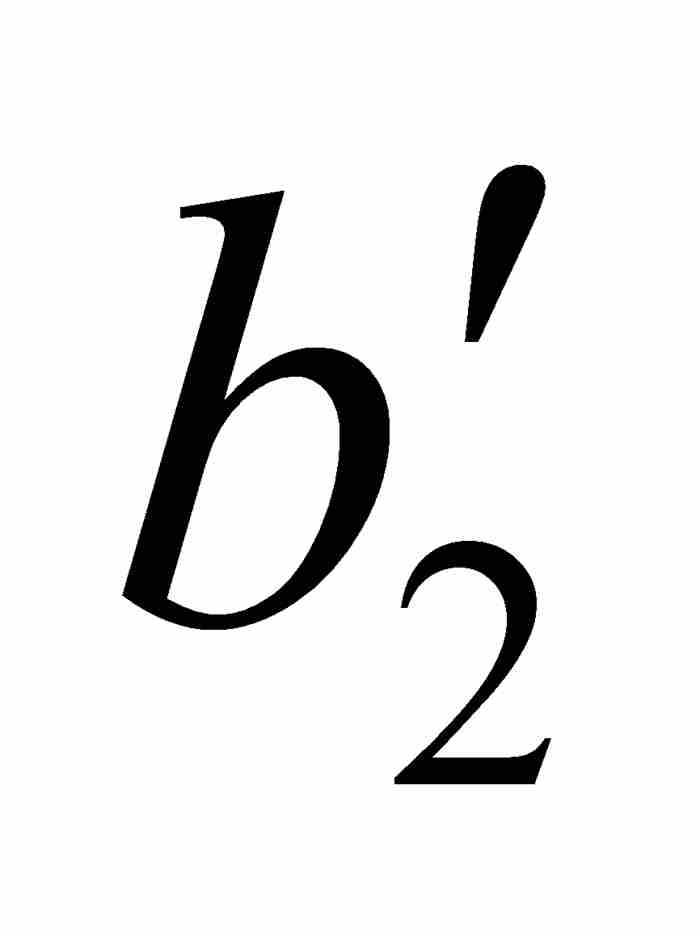]中的任何點x和y，有

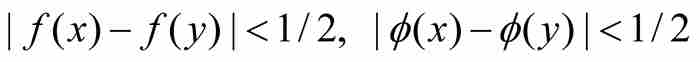
他用ε = 1/8, 1/16, …, 1/2k, …繼續作下去，由此產生一個閉區間序列[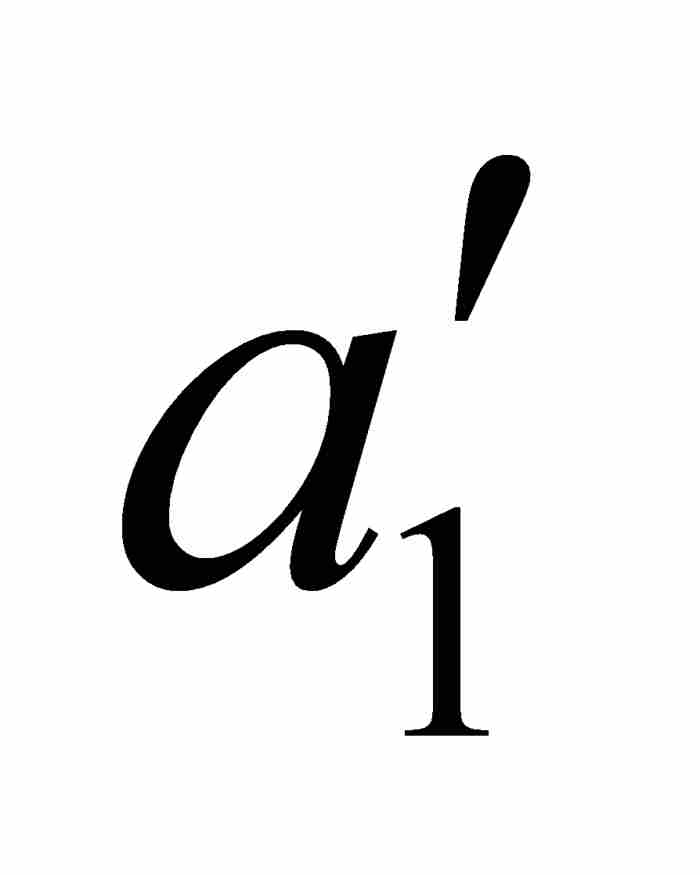, 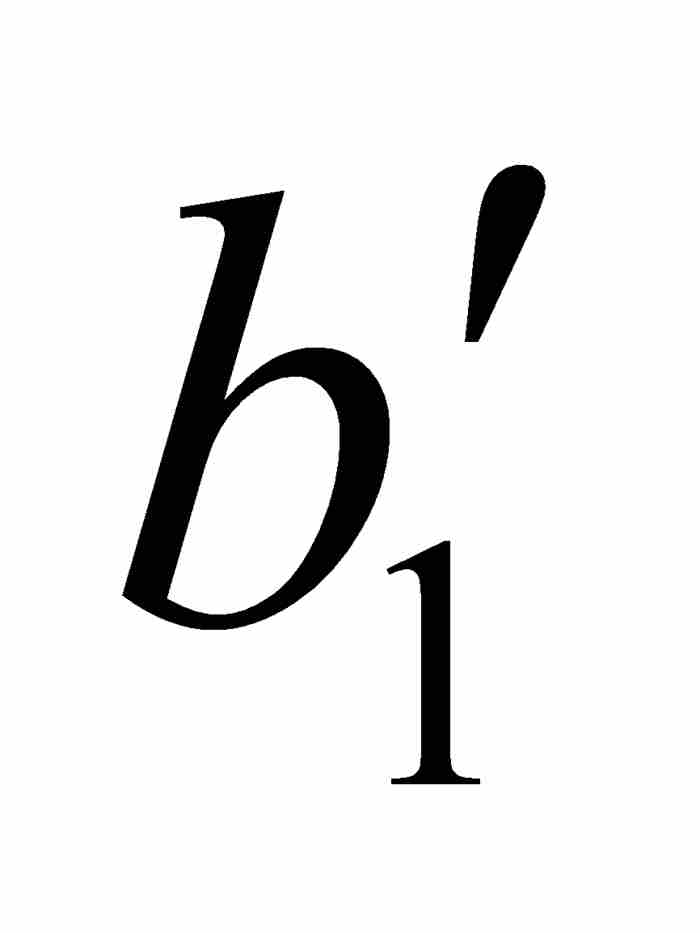] ⊃ [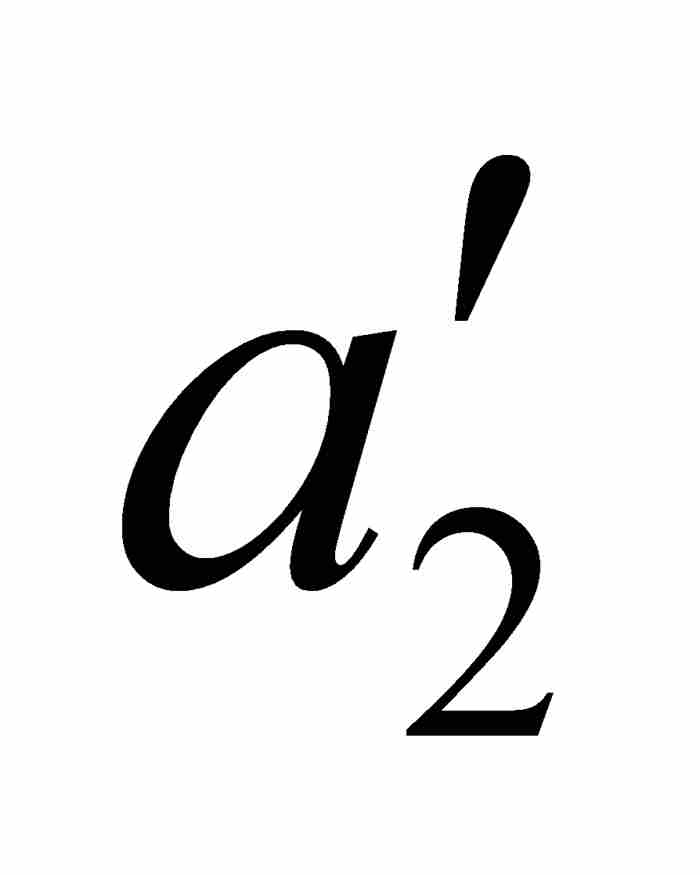, 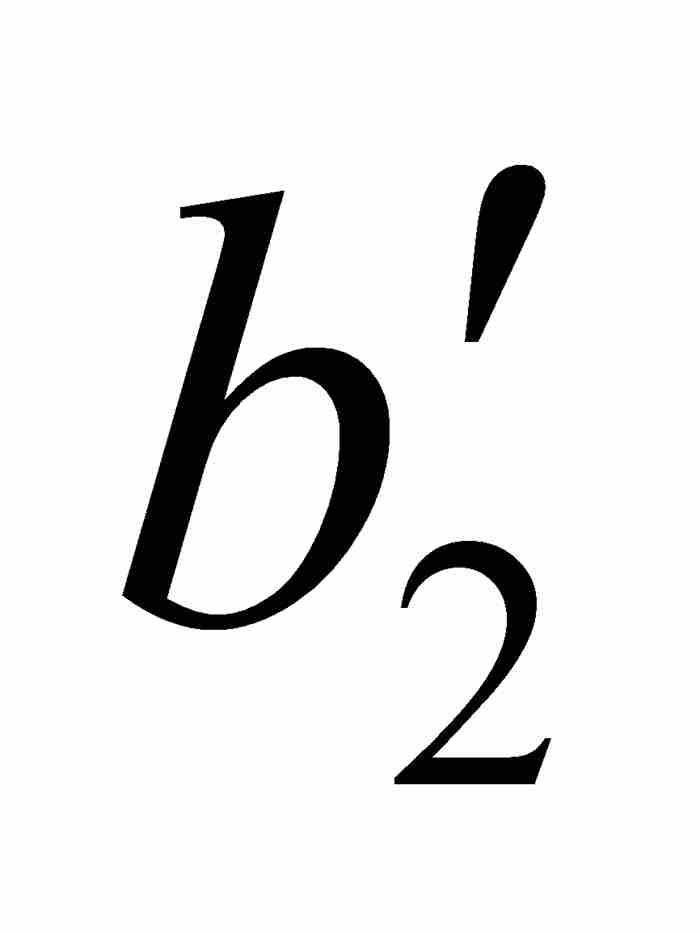] ⊃ [, 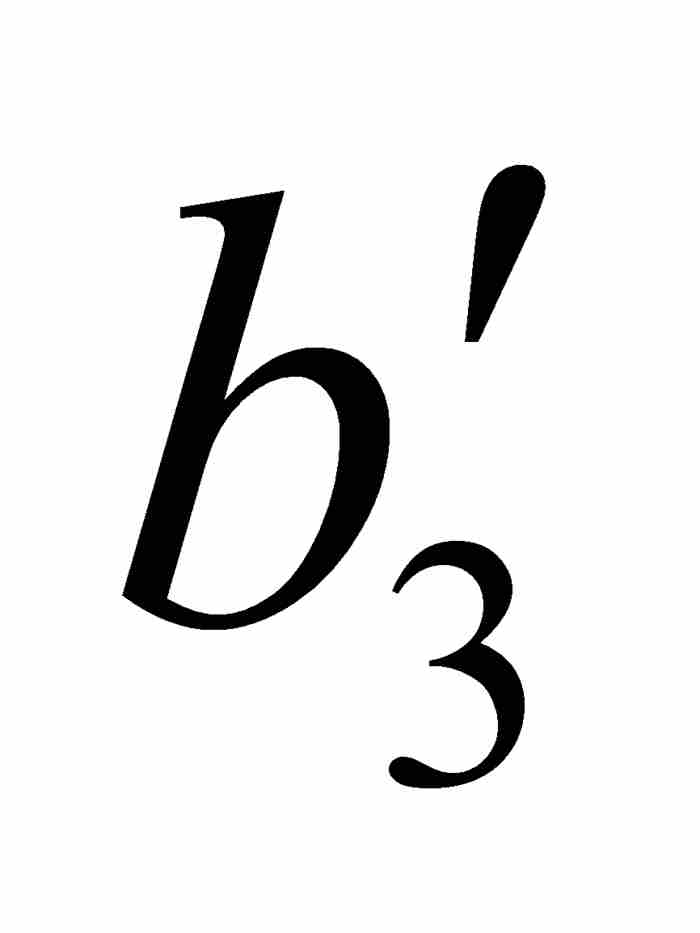] ⊃ …，使得對於[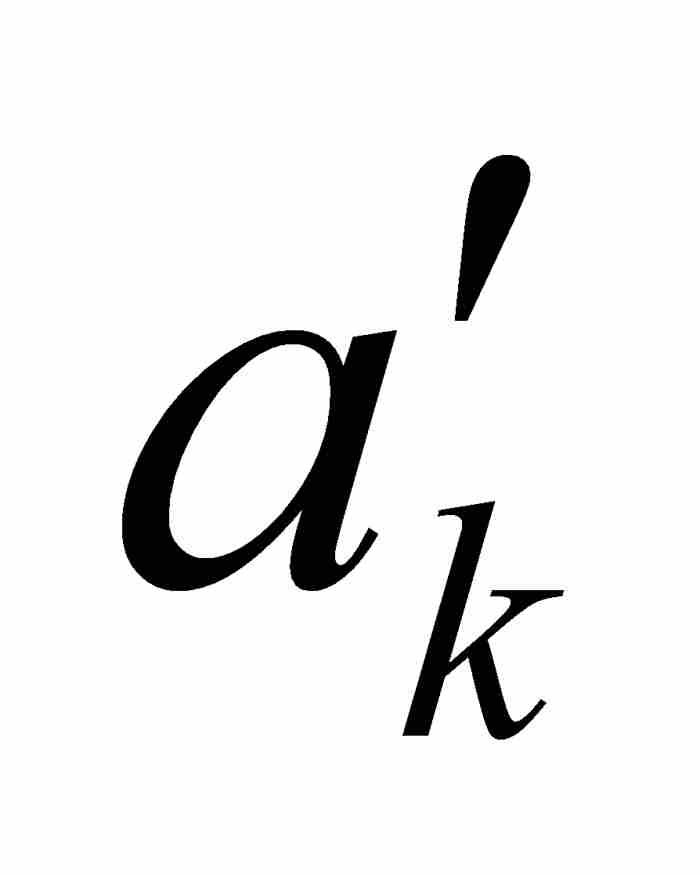, 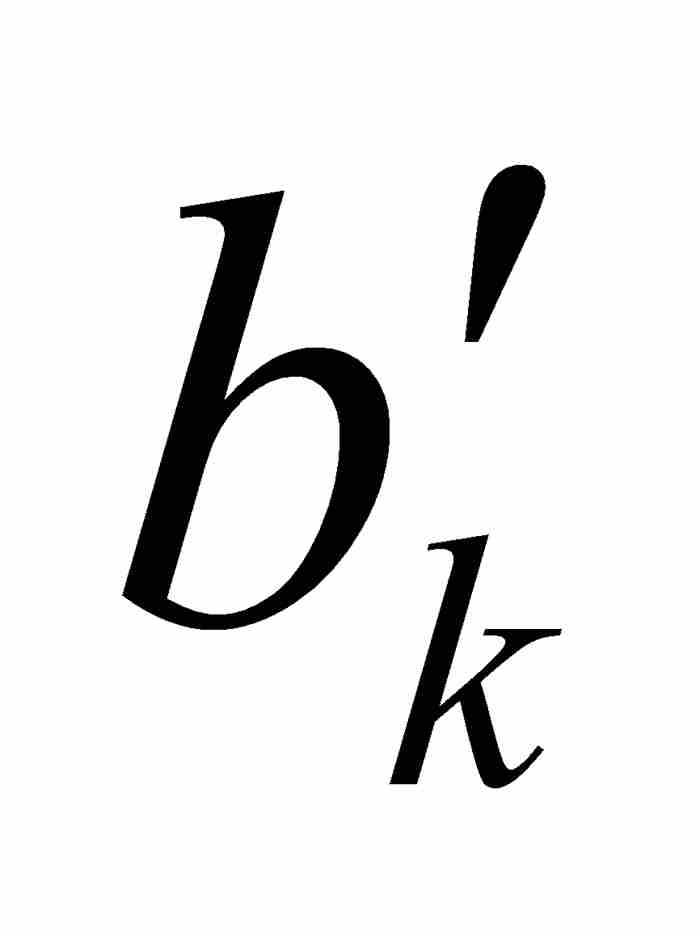]中的任何點x和y，有

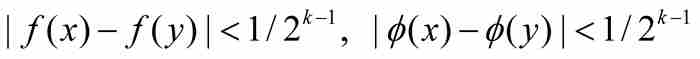（2）

一個矛盾隨即發生。根據實數的完備性性質，在所有嵌套的區間[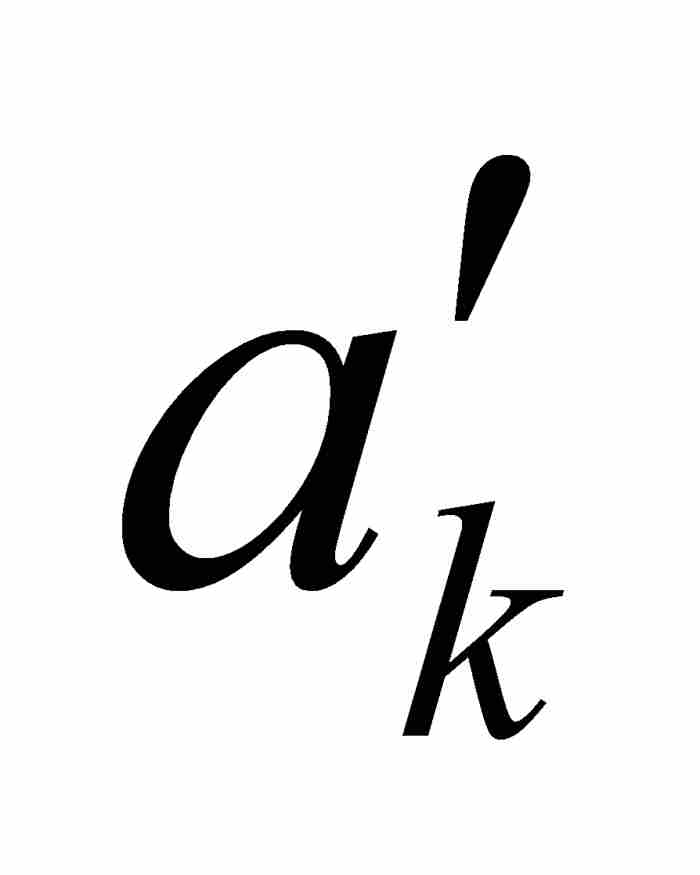, 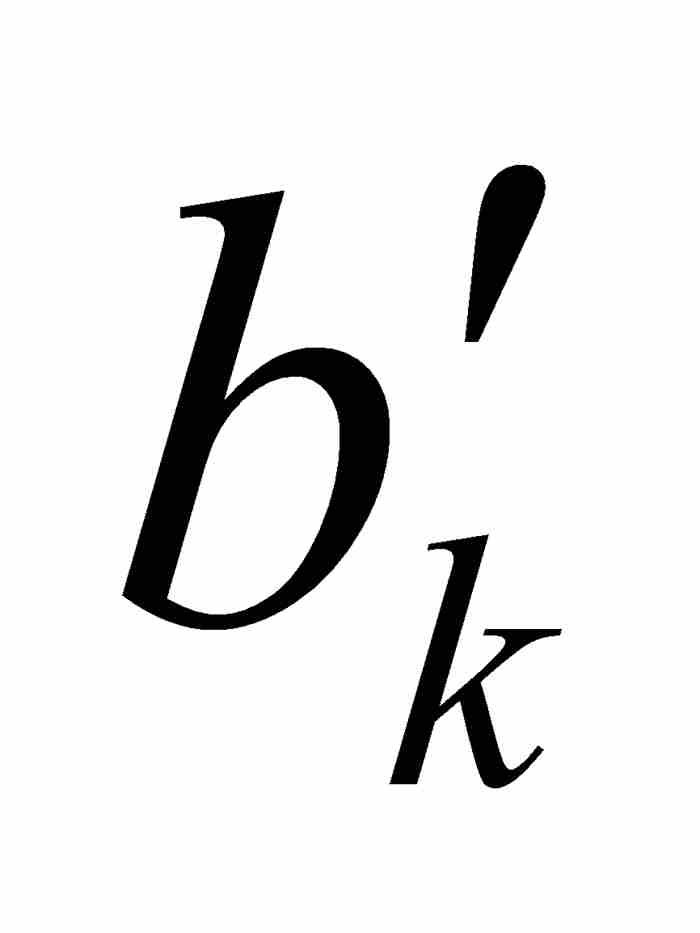]中必定存在一個公共點c。由於c位於[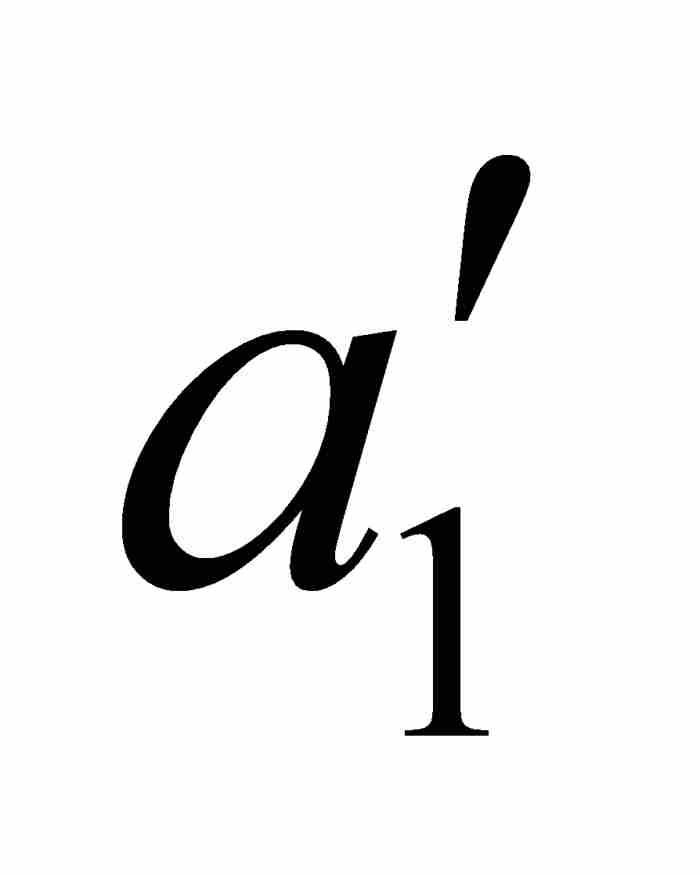, 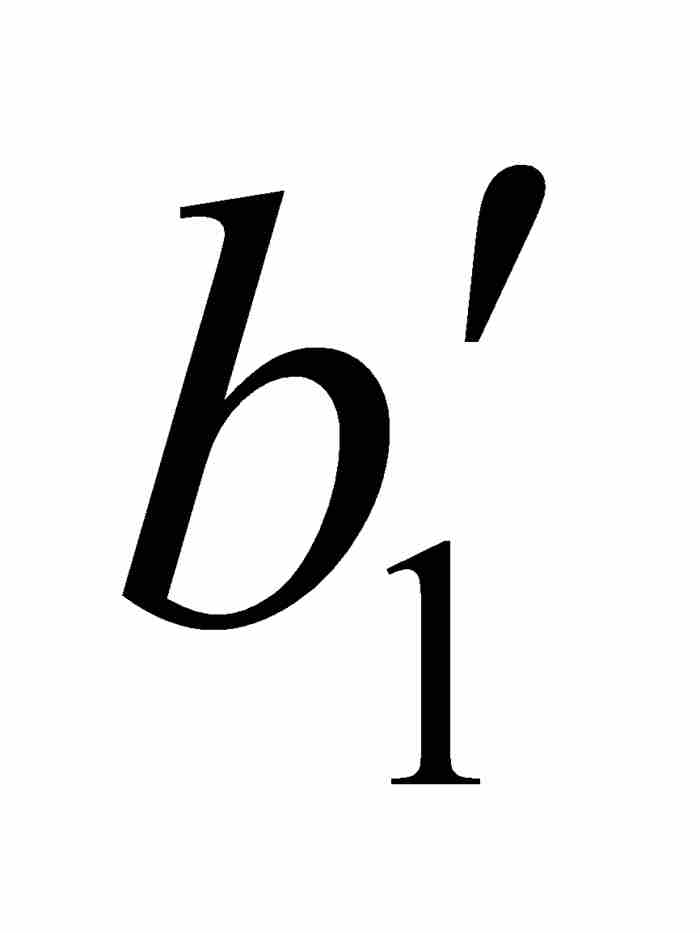]內，它實際是在我們原來的區間（a, b）內。

接下來我們斷定f在c是連續的。這是很容易得出的結論，因為沃爾泰拉在構造他的嵌套的區間序列時已經控制了f的振幅。為了作出嚴格的魏爾斯特拉斯ε - δ 方法的證明，我們可取任意 ε > 0，並且選擇一個滿足1/2k-1 < ε 的自然數k。我們確知c是區間[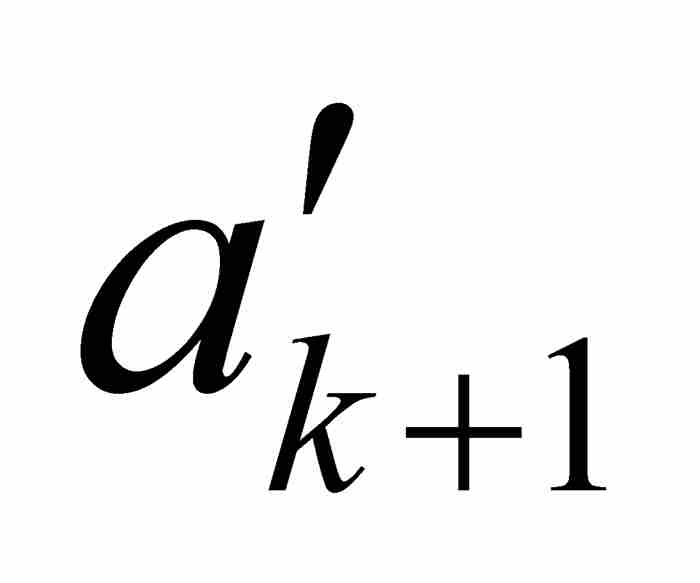, 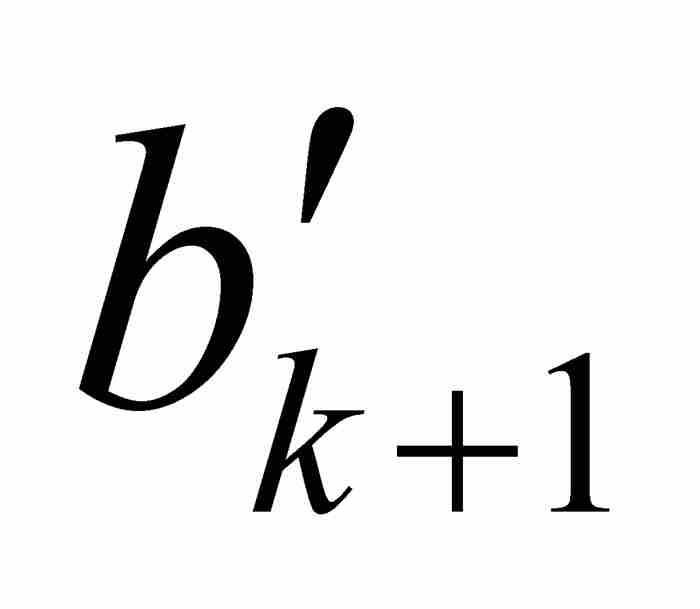]中的一點，而這個區間又是在開區間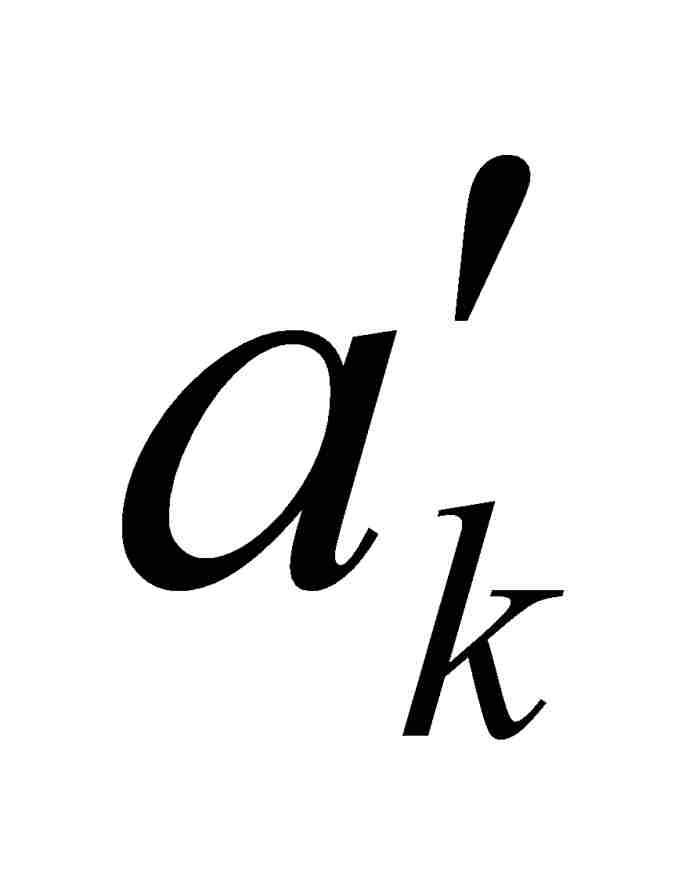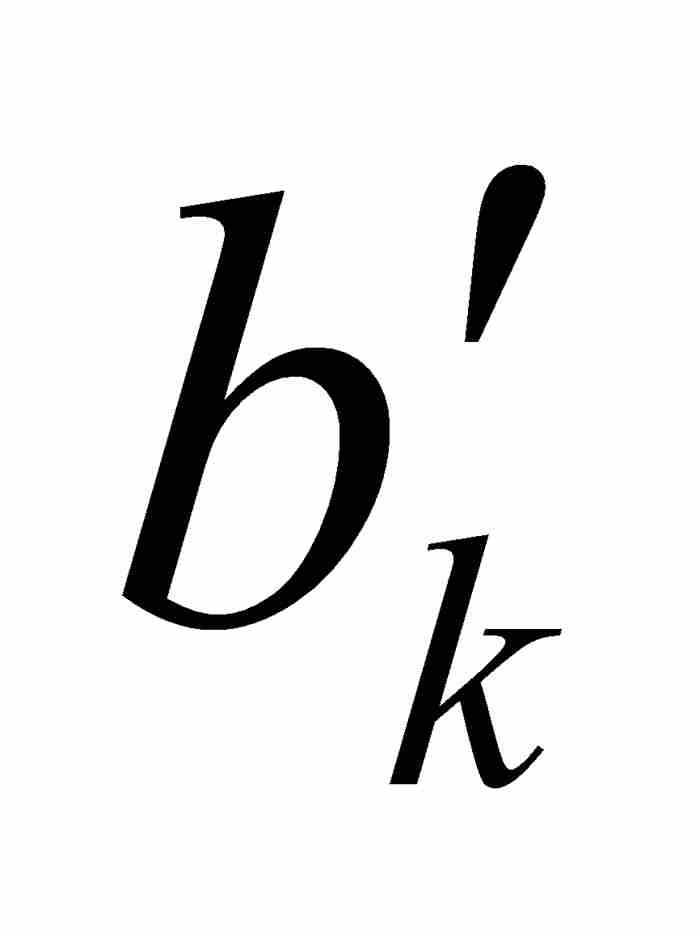（, ）內，所以可以求出一個δ > 0，使（c - δ, c + δ 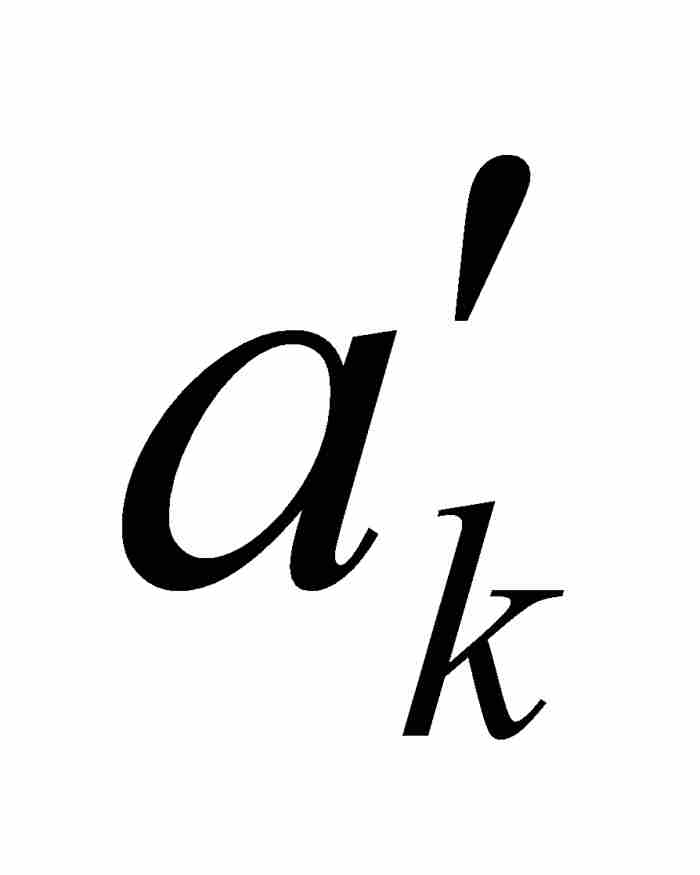）⊂（, ）⊂ [, ]。因此，對於滿足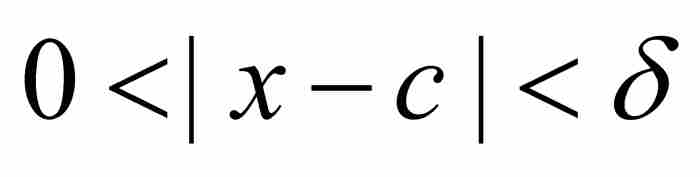的任何x，根據式（2）我們有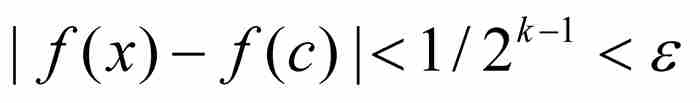。這就證明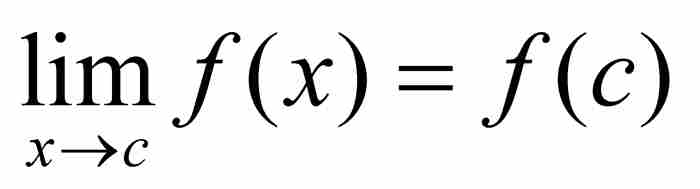，所以f在c是連續的，這正是我們要推斷的結果。

由於可以把同樣的論證一字不改地用於φ，所以 φ 在c也是連續的。用這種方法，我們已經引出一個矛盾，因為c同時屬於C_f和C_φ，違反一個函數的連續性點是另外一個函數的非連續性點的假定。所以別無選擇，我們只能斷定不可能存在兩個這樣的點態不連續函數。

在繼續討論之前，我們需要作兩點說明。首先，沃爾泰拉對於區間[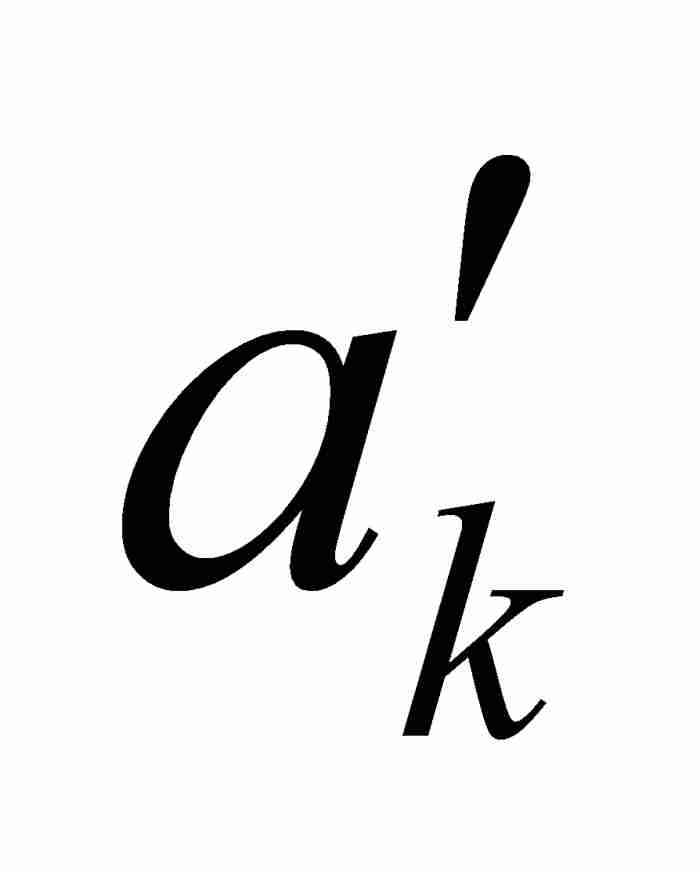, 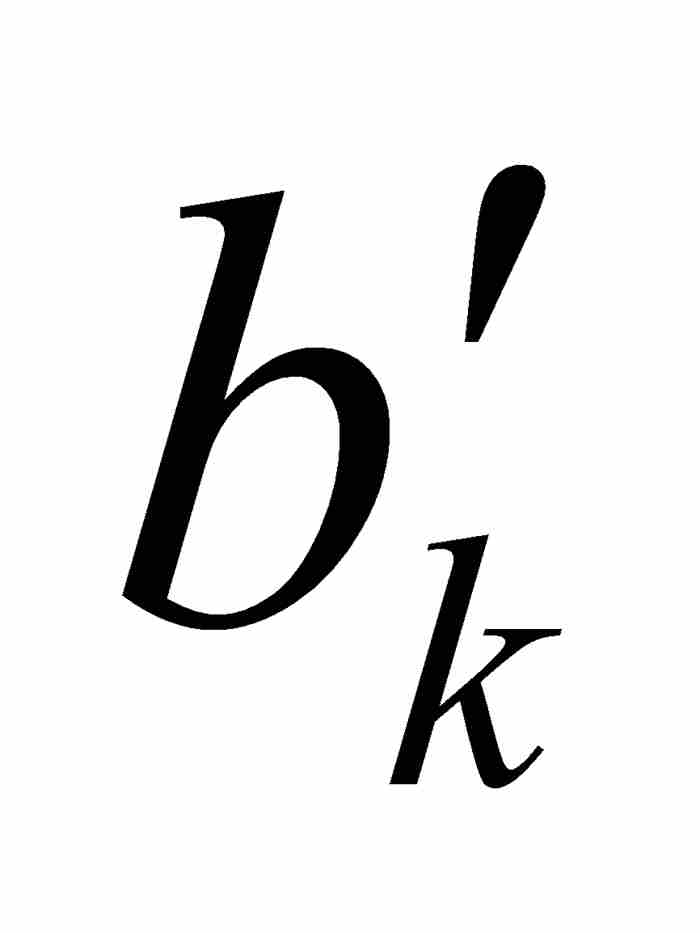]沒有明確要求為閉區間。這是一個容易補救的疏忽，正如我們在上面所作的那樣。其次，在前面的例子中，函數H的連續性點是函數K的非連續性點，反過來也是一樣，我們注意到K是完全不連續函數（漢克爾的3B類函數）而不是點態不連續函數（漢克爾的3A類函數）。因此，那個例子同沃爾泰拉證明的結果絲毫不相牴觸——恐怕任何人都會因這個結果而難以入眠。

沃爾泰拉從他的定理得出兩個重要的推論。第一個推論解決了分析學中的一個主要問題，我們把它陳述如下。

推論1　由於存在一個在每個無理數點連續而在每個有理數點不連續的函數，也就不可能找到一個在每個無理數點不連續而在每個有理數點連續的函數。2

2 Vito Volterra, Opere Mathematiche, vol.1, Accademia Nazionale dei Lincei, 1954, p. 8。

為了充實他的論證的細節，我們設想這樣一個函數G(x)，它的C_G是有理數集（稠密集）。那麼，G是點態不連續的。但是我們已在前面遇見了擴充的直尺函數R(x)，它也是點態不連續的，其C_R卻是無理數集。於是G的連續性點將是R的非連續性點，同沃爾泰拉的定理矛盾。因此，這兩個函數不可能同時存在。由於直尺函數確實是存在的，所以我們不得不作出函數G不存在的結論。套用一句西部電影中對牛仔們的評論，沃爾泰拉的定理證明了「這座城市沒有大到足以同時容納他們兩人」。一個函數僅在有理數點上連續從邏輯上說是不可能的。

所以，病態函數是有其限度而不是無所不包的。無論數學家們如何精明，某些函數仍然置身其外，這就是沃爾泰拉用這個巧妙的論證所證實的一個事實。但是，他還得到一個隱含的推論，那就是不可能存在無理數點上取有理數並且反過來在有理數點上取無理數的連續函數。3

3 Vito Volterra, Opere Mathematiche, vol.1, Accademia Nazionale dei Lincei, 1954, p. 9。

推論2　地不存在在實數集上定義的這樣一個連續函數g(x)，當x取無理數時g(x)為有理數，而當x取有理數時g(x)為無理數。

證明　為了導致矛盾，沃爾泰拉再次假定存在這樣一個函數g。然後通過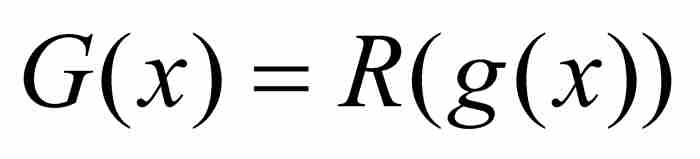，其中R是前面所說的擴充的直尺函數，並且給出關於G的兩個斷言。

斷言1　如果x為有理數，那麼G在x是連續的。

這是顯而易見的，因為只要x為有理數，g(x)就是無理數，所以R在g(x)是連續的。但是假定g是處處連續的，所以復合函數G在x將是連續的。

斷言2　如果y為無理數，那麼G在y是不連續的。

通過選擇一個收斂於y的有理數序列{x_k}，就知道這是很容易證實的。在這種情況下，

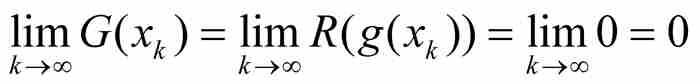
這是因為g把每個有理數x_k變換成一個無理數g(x_k)，而直尺函數R在無理數點的值為零。另一方面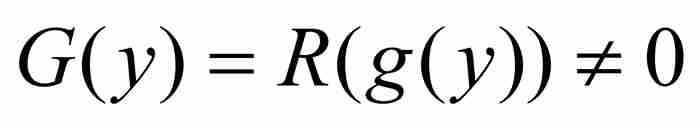，，因為g(y)為有理數。總之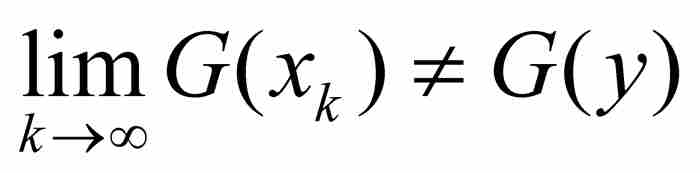，，所以G在y是不連續的。

把這兩個斷言結合起來，就證明了函數G在有理數點是連續的而在無理數點是不連續的——這是沃爾泰拉剛才證明不可能出現的一種局面！由此推斷不可能存在像g這樣的一個函數。所以，沒有一個連續函數能夠把有理數變換為無理數，同時反過來把無理數變換為有理數。

這些結果尤其使我們想起，雖然有理數集和無理數集都是實數的稠密集，但是它們在本質上是不可互換的。正如我們所見，康托爾曾經特別指出有理數是可數的而無理數是不可數的事實，但是事情並不止於此，數學家們還發現這兩個數系之間存在某些更微妙的差別。這些差別之一是一個集合的「類型」的概念。集合的類型是由沃爾泰拉的天才學生勒內·貝爾提出的概念，他是我們在下一章介紹的數學家。

我們謹以這些敘述告別那時年僅21歲的維托·沃爾泰拉。擺在他面前的是遠大而輝煌的事業，人們將會見到他繼續取得數學上的成功，並得到國際上的公認，而英國國王喬治五世甚至授予他榮譽爵士稱號。

追溯沃爾泰拉的後半生，我們知道他賦予19世紀以「函數論世紀」的特徵。4 從歐拉最初提出函數的思想開始，函數概念在柯西、黎曼和魏爾斯特拉斯的研究中扮演主要角色，並且接著傳承給新一代的康托爾、漢克爾以及沃爾泰拉本人。函數在分析學中處於至高無上的支配地位，而在函數中發現的種種意想不到的可能性，無不一次又一次地使數學家們驚詫莫名。如我們所知，由於沃爾泰拉在1881年的兩項不同而又迷人的發現，使他在我們敘述的故事中佔有重要的一席之地。

4 Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 1023。

對於這位年輕人說來，1881年是非同尋常的一年。