
卡爾·魏爾斯特拉斯(1815—1897)
正如我們所知,在19世紀,數學家們將微積分的嚴格性提高到一個新的水平。然而,按照我們今天的標準,這些成就並不是無可挑剔的。當你拜讀那個時期的數學文獻時,猶如聆聽音樂大師肖邦在一架三兩琴鍵失調的鋼琴上演奏樂章,固然能夠怡然自得地鑒賞音樂的神韻,不過間或也會聽到些許畸變之音。只有在微積分中消除不精確性的最後痕跡,分析論證變成對於一切實用目的都是無可置疑的時候,數學的新紀元才能到來。魏爾斯特拉斯是實現這個最後轉變的最大功臣。
魏爾斯特拉斯沿著一條非傳統的道路嶄露頭角。他在學生時代,成績並不優異,卻熱衷於狂飲啤酒和擊劍。到30歲時,魏爾斯特拉斯成為德國一所偏僻的大學預科學校(高級中學)的教師,這所學校遠離歐洲的學術中心。在白天,他對學生講授算術和書法,只有在課餘且批改完學生的作業之後,年輕的魏爾斯特拉斯方能致力於他的數學研究。1
1 這段傳略摘自Dictionary of Scientific Biography, vol. XIV, C. C. Gillispie, editor-in-chief, Scribner, 1976, pp. 219-224。
這位名不見經傳的來自德國一個不知名小鎮的中學教師,在1854年發表了一篇關於阿貝爾積分的論文。凡是讀過這篇文章的數學家,無不驚訝萬分。很明顯,這篇論文的作者,必定是具有非凡天賦的奇才。不出兩年,魏爾斯特拉斯在柏林大學謀求到一個職位,受聘為這所大學的教授,並躋身於世界傑出數學家的行列。他的事跡,算得上是一個真實灰姑娘的故事。
魏爾斯特拉斯對分析學作出的貢獻是極為顯著的,正如他的教學方法是舉世聞名的一樣。隨著他的赫赫名聲在德國和歐洲的傳播,這位數學大師吸引著渴望師從他的年輕數學家們。在他的門下雲集了一大批追隨者。那時人們可以見到這樣一種真實的場景,患有嚴重眩暈症的魏爾斯特拉斯坐在一把安樂椅上授課,而由一名指派的學生把他的話寫在黑板上。(這樣一種講課方式令後來的教授們羨慕不已,然而是幾乎無法重現的。)
如果說魏爾斯特拉斯的執教風格是異乎尋常的話,那麼他對待發表研究成果的態度也是與眾不同的。儘管他的講課充滿了新穎的觀點和重要概念,但是他疏於發表文章,而是經常讓別人從他們自己的著述中去傳播這樣的知識。因此人們發現,他的成果是籠統地屬於魏爾斯特拉斯學派的。那些信仰「不發表就是毀滅」的現代學者們,很難理解這種非佔有式的學術觀念。魏爾斯特拉斯以創立具有重大意義的數學為己任,寧願去冒毀滅的風險。
魏爾斯特拉斯學派通過魏爾斯特拉斯本人或者他的門生們發表的研究成果,對分析學賦予邏輯上的一種無與倫比的精確性。他矯正了許多難以捉摸的錯誤概念,證明了大量重要的定理,並且構造出一個令數學家們驚歎不已的處處連續而又不可微的函數的反例。在這一章,我們會瞭解到卡爾·魏爾斯特拉斯為什麼被譽為「現代分析學之父」。2
2 Eric Temple Bell, Men of Mathematics, Simon & Schuster, 1937, p. 406。
回到基本問題
不妨回憶一下,柯西是怎樣在極限的基礎上建立他的微積分的。在他給出的定義中有這樣一句話:
當屬於一個變量的相繼值無限地趨近某個固定值時,如果以這樣一種方式告終,變量值同固定值之差小到我們希望的任意小,那麼這個固定值就稱為其他所有值的極限。
對於我們而言,這句話的某些方面,例如 「趨近」這個行動,似乎不是一種令人滿意的表達方式。趨近是指某種實際的動作嗎?如果是這樣,那麼在談論極限之前我們必須考慮時間和空間的概念嗎?此外,這個過程「告終」的含義是什麼?總之,所有這一切尚需作最後修訂。
魏爾斯特拉斯重新給出極限的定義:
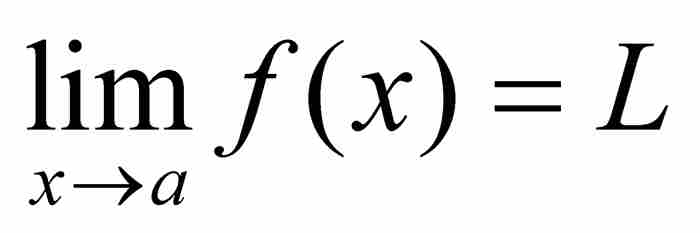 ,當且僅當對於任意ε > 0,存在一個δ > 0,
,當且僅當對於任意ε > 0,存在一個δ > 0,
使得只要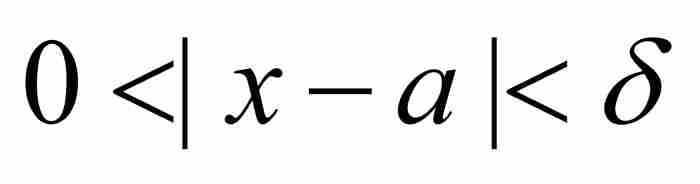 ,就有
,就有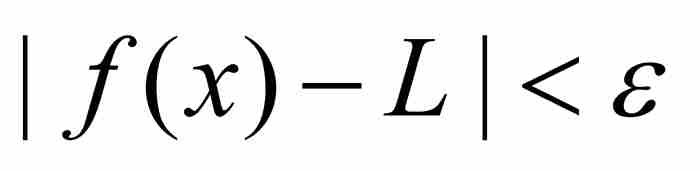 (1)
(1)
這個完美的定義同柯西對極限所說的話形成鮮明對比。在這裡,沒有任何動作,而且不涉及時間。這是一個靜態的而非動態的定義,同時又是一個代數的而非幾何的定義。定義的核心是一個關於不等式的斷言。並且,可以把這個定義作為證明各種極限定理的基礎,例如,用它給出「和的極限等於極限的和」的確切證明。至此,對於這樣的定理可以進行像歐幾里得命題那樣完全嚴格的證明。
有人可能提出這樣的觀點:需要為精確性付出某種代價,因為魏爾斯特拉斯提出的嚴格定義缺乏直覺的魅力和幾何上的直觀性。毫無疑問,還需要慢慢適應像式(1)這樣的陳述。除此之外,幾何直觀是值得懷疑的,而魏爾斯特拉斯給出的這個純粹的分析定義絲毫不牽涉空間與時間。
魏爾斯特拉斯除了重新闡明各種關鍵性概念外,還領會到了這些概念的含義,這是他的前輩們未能做到的。一個例子就是一致連續性,柯西同這種函數性質失之交臂。我們回憶一下,柯西在逐點的基礎上定義了連續性,他指出,如果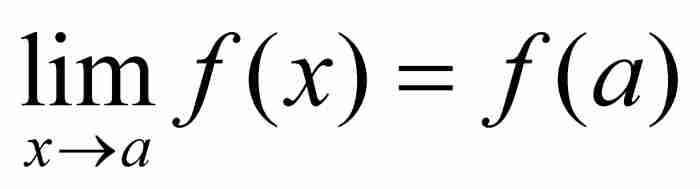 ,那麼f在a是連續的。採用魏爾斯特拉斯的語言,這意味著對於每個ε > 0,存在一個對應的δ > 0,使得只要
,那麼f在a是連續的。採用魏爾斯特拉斯的語言,這意味著對於每個ε > 0,存在一個對應的δ > 0,使得只要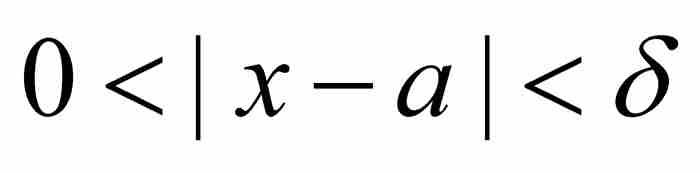 ,就有
,就有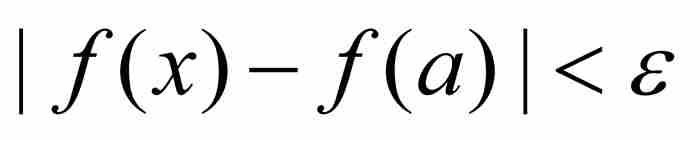 。因此,對於一個固定的「靶子」ε 和一個已知的a,我們能夠求出所需的δ。但是此處的δ 同時依賴ε 和a。當考慮一個不同的a值時,我們如果保持同一個ε,一般而言,必須調整對δ 的選擇。
。因此,對於一個固定的「靶子」ε 和一個已知的a,我們能夠求出所需的δ。但是此處的δ 同時依賴ε 和a。當考慮一個不同的a值時,我們如果保持同一個ε,一般而言,必須調整對δ 的選擇。
愛德華·海涅(1821—1881)在出版物中首次作出這種區分,不過他暗示「這個普遍概念」是他的良師益友魏爾斯特拉斯傳授給他的。1海涅給出了一致連續的定義:如果對於每個ε > 0,存在一個δ > 0,使得函數f的定義域內的任意兩點x和y,只要它們的距離小於δ,就有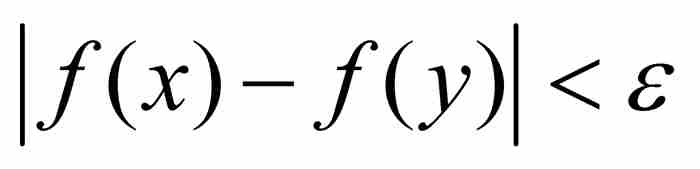 ,那麼 f 在其定義域上是一致連續的。在本質上,這意味著「一個δ適用於所有ε」,所以在這個一致距離之內的點,它們之間的函數值之差將在ε的範圍內。
,那麼 f 在其定義域上是一致連續的。在本質上,這意味著「一個δ適用於所有ε」,所以在這個一致距離之內的點,它們之間的函數值之差將在ε的範圍內。
1 E. Hairer and G. Wanner, Analysis by Its History, Springer- Verlag, 1996, p. 215。
顯然,一個一致連續的函數,在每個單獨的點是連續的。但是,相反的結論並不成立,典型的反例是定義在開區間(0, 1)上的函數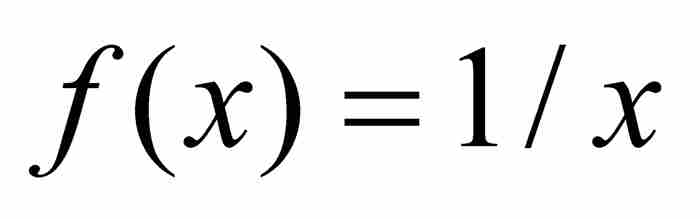 ,如圖9-1所示。這個函數在(0, 1)內的每個點無疑是連續的,但是它不符合海涅的一致連續判別準則。我們考察一下何以如此。令ε = 1,我們斷定不會存在一個δ > 0,使得當從(0, 1)選擇滿足
,如圖9-1所示。這個函數在(0, 1)內的每個點無疑是連續的,但是它不符合海涅的一致連續判別準則。我們考察一下何以如此。令ε = 1,我們斷定不會存在一個δ > 0,使得當從(0, 1)選擇滿足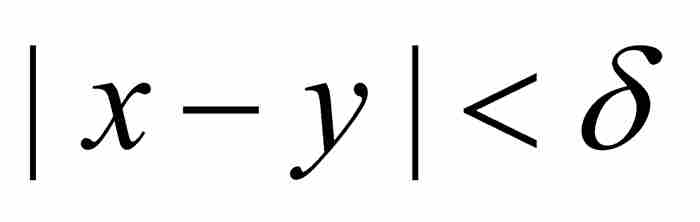 的x和y時,有
的x和y時,有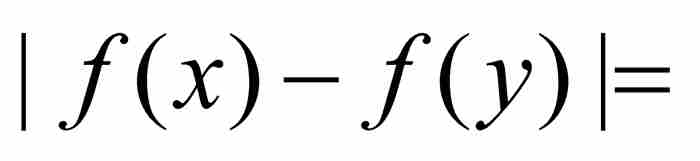
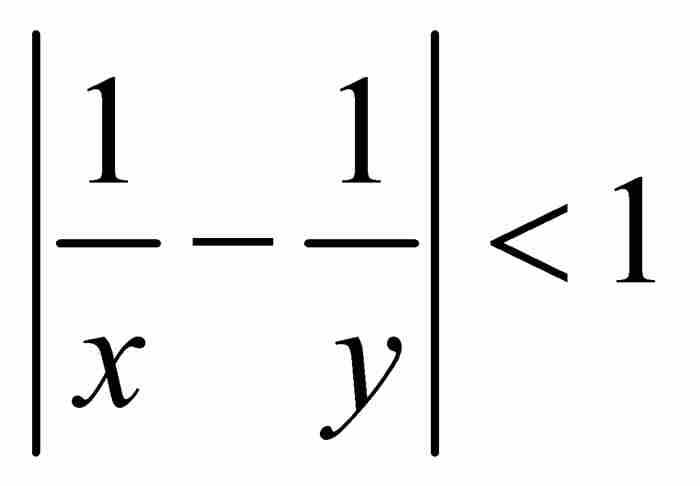 。這是因為,對於給定的δ,我們可以選擇一個整數
。這是因為,對於給定的δ,我們可以選擇一個整數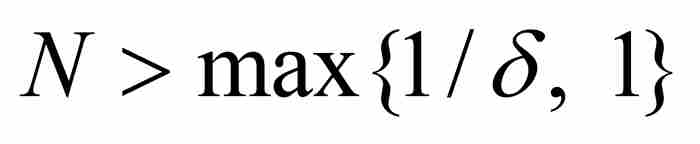 ,並且令
,並且令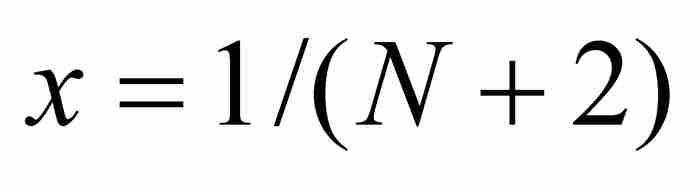 和
和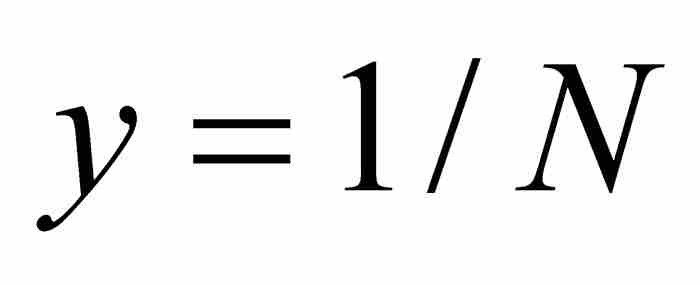 。在這種情形下,x和y同屬於區間(0, 1),並且有
。在這種情形下,x和y同屬於區間(0, 1),並且有
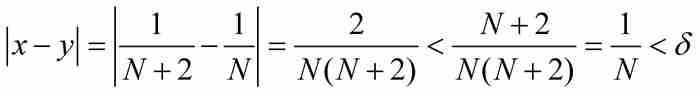
然而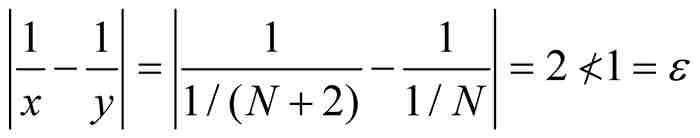 。一致連續的條件不滿足。
。一致連續的條件不滿足。
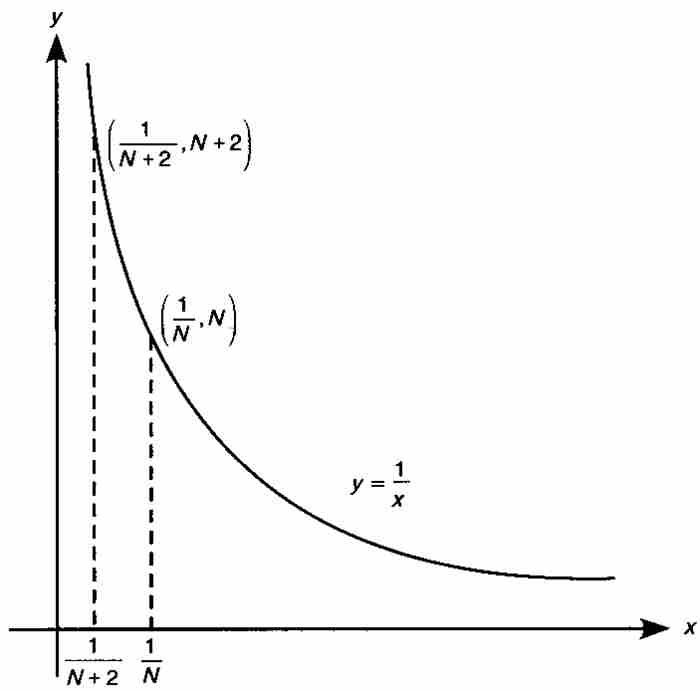
圖 9-1
回顧第6章,不禁使我們想起柯西曾經論述過連續函數,同時,在他的某些證明中實際上使用了一致連續性。值得慶幸的是,當海涅在1872年證明了一個有界閉區間[a, b]上的連續函數必定是一致連續函數時,一場邏輯推理上的災難得以避免。就是說,如果我們把函數限制在閉區間[a, b]上,那麼連續性同一致連續性之間的差異將隨之消失。(請注意,在上面舉出的反例中,函數是定義在一個開區間上的。)所以,對於有界閉區間上的函數,當在證明中出現柯西的錯誤概念時,多虧海涅的結果,這使他的證明是「可補救的」。
魏爾斯特拉斯認識到一種更為重要的區分,那就是點態收斂同一致收斂之間的差異。為了考察這兩種收斂概念,我們有必要暫且離開一下正題。
假定我們有一個函數序列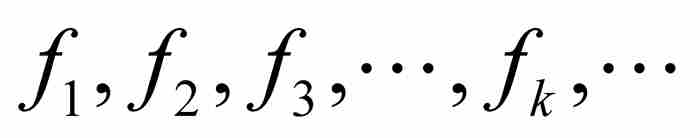 ,它們具有相同的定義域。如果在這個定義域中固定一點x,並且把它代入每個函數,遂產生一個數列
,它們具有相同的定義域。如果在這個定義域中固定一點x,並且把它代入每個函數,遂產生一個數列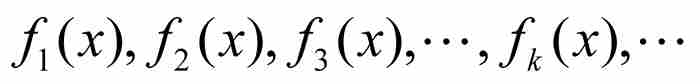 。假定對於每個單獨的x,這個數列收斂。在這種情況下,在每個點x建立了由
。假定對於每個單獨的x,這個數列收斂。在這種情況下,在每個點x建立了由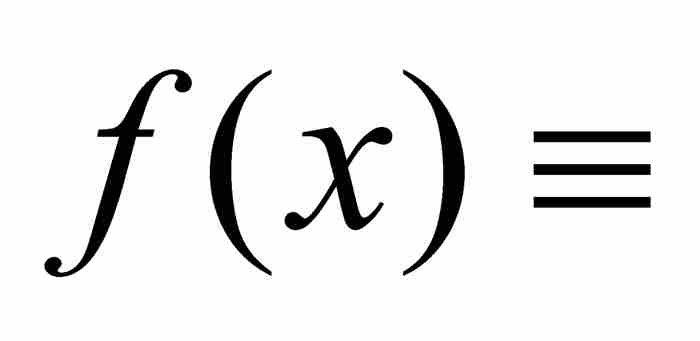
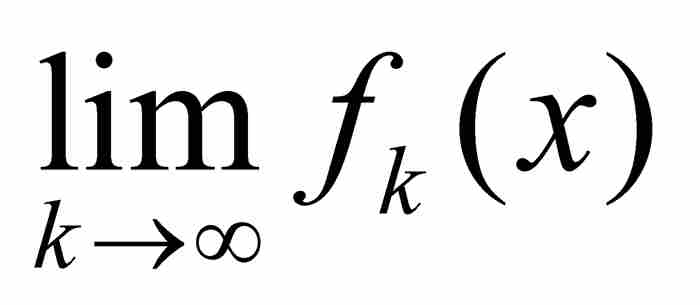 定義的新函數。我們把
定義的新函數。我們把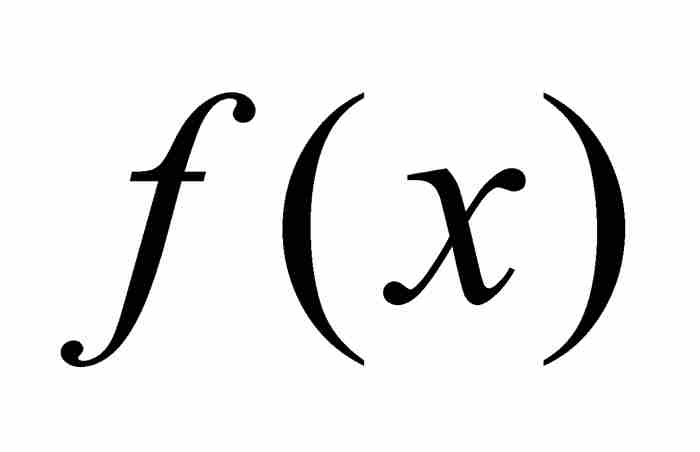 稱為
稱為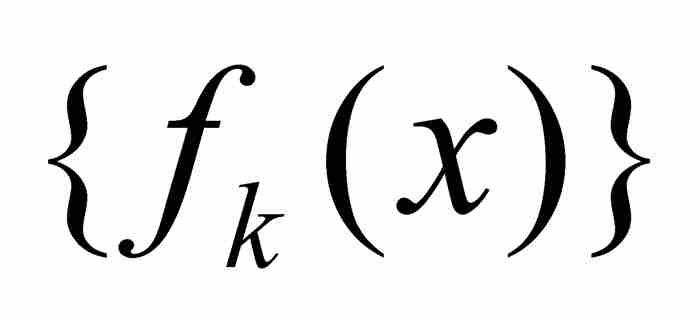 的「點態極限」。
的「點態極限」。
例如,考慮在區間[0, π]上定義的函數序列:
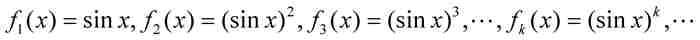
這個序列的前三個函數的圖形在圖9-2中畫出。
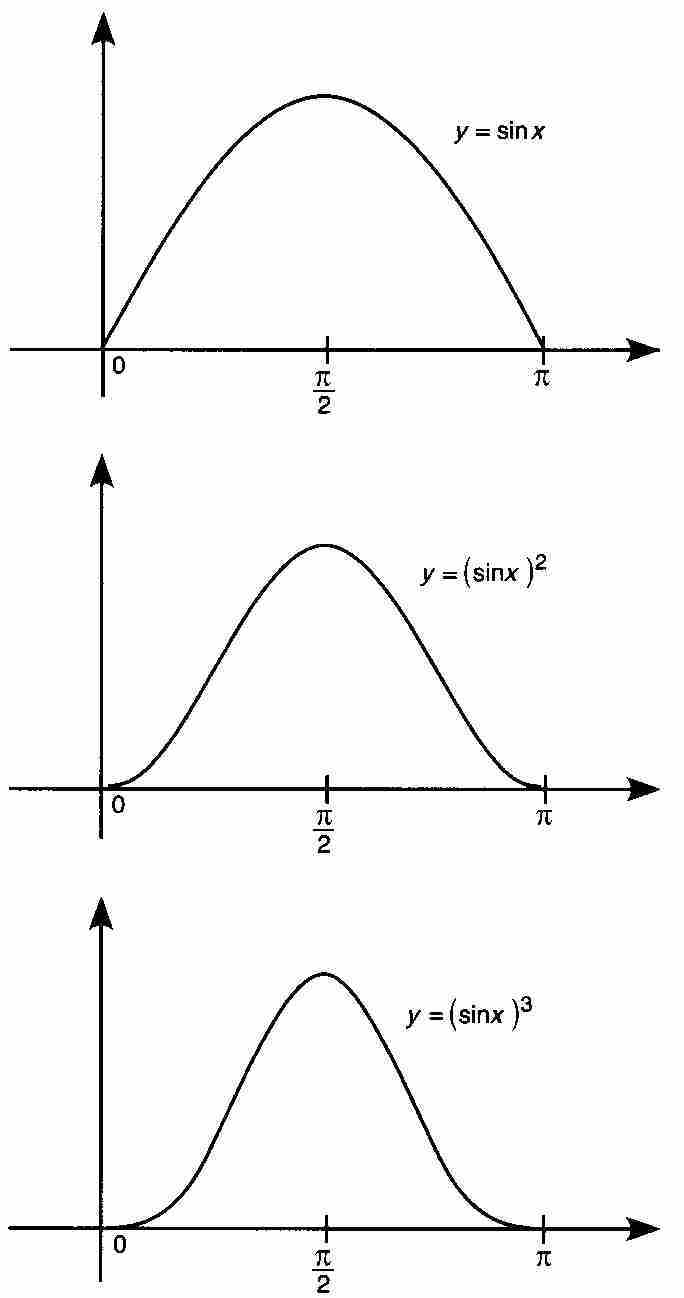
圖 9-2
我們看出,對於所有k≥1,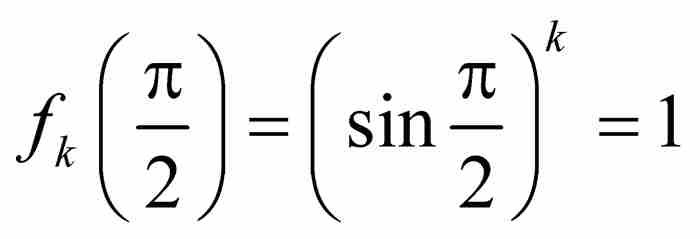 ,所以
,所以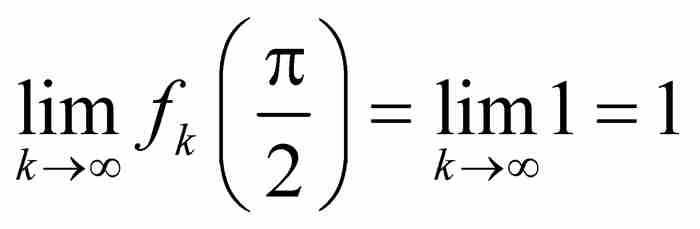 。另一方面,如果x在區間[0, π]內,但是
。另一方面,如果x在區間[0, π]內,但是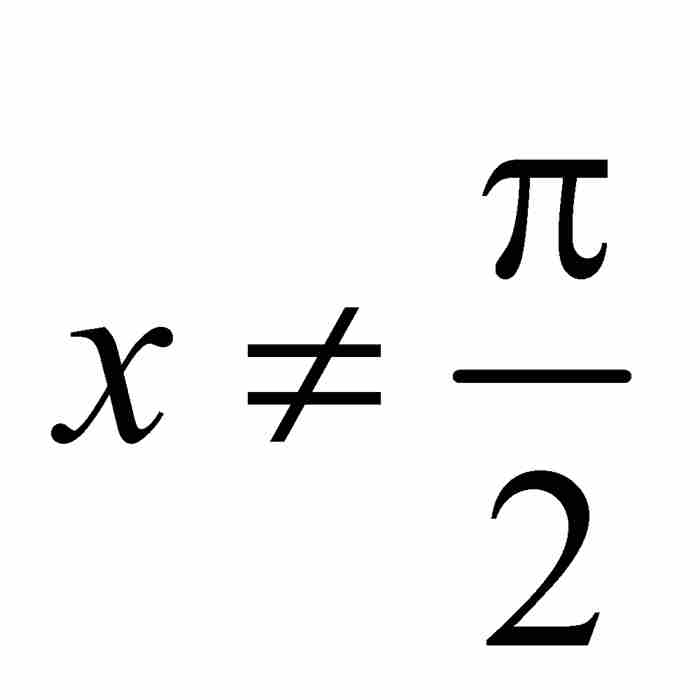 ,那麼
,那麼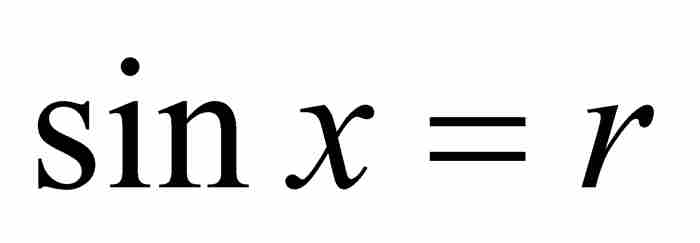 ,其中
,其中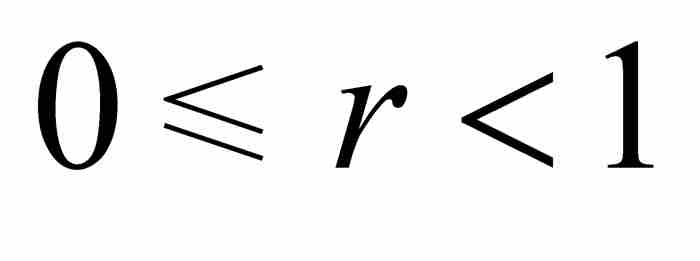 ,所以
,所以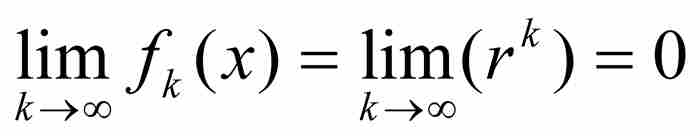 。因此,這個點態極限為
。因此,這個點態極限為
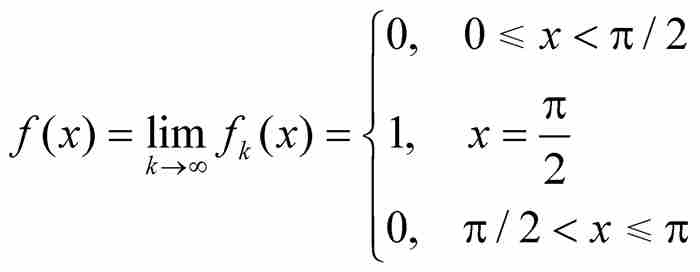
它的圖形顯示在圖9-3中。
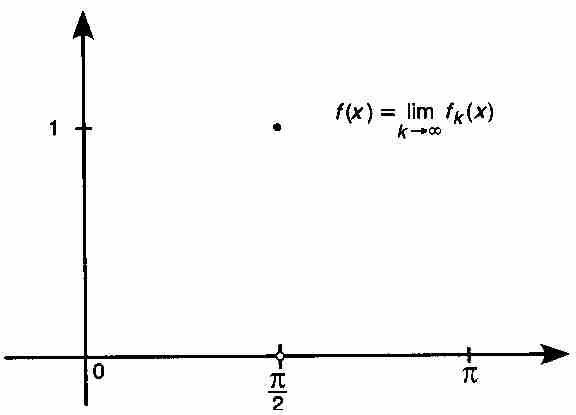
圖 9-3
這個例子引出分析學中的一個重大問題:如果函數序列{fk}中的每個函數具有某種確定的性質,而f是這個函數序列的點態極限,那麼f本身必須具備這種性質嗎?用數學語言表述,就是問函數的一種特性是否由點態極限繼承。如果每個fk是連續函數,f必定是連續函數嗎?如果每個fk是可積的,f必定是可積的嗎?
要是單憑直覺,可能回答「是的,為什麼不是呢!」可惜,世間的事物並非如此簡單。例如,連續性就不是點態極限函數繼承的特性,這正是使過去的柯西和其他數學家迷惑不解的根源。2 我們只需考察一下上面的例子就會明白,函數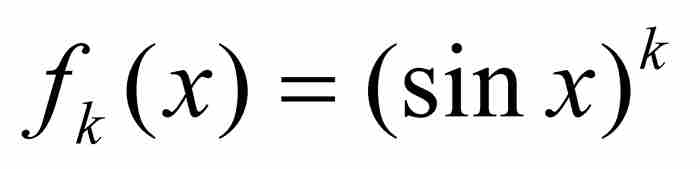 是處處連續的,然而它們在圖9-3中的點態極限
是處處連續的,然而它們在圖9-3中的點態極限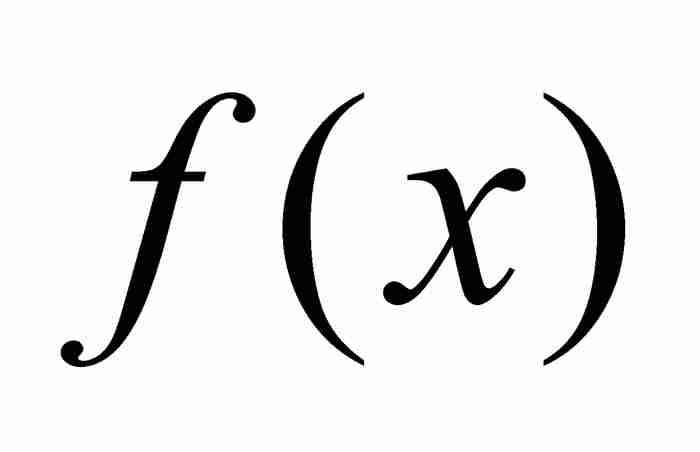 在
在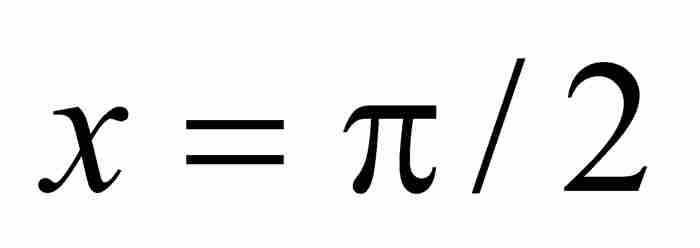 就是不連續的。這個例子同樣說明,可微性也不是點態極限繼承的特性。
就是不連續的。這個例子同樣說明,可微性也不是點態極限繼承的特性。
2 Augustin-Louis Cauchy, Oeuvres, ser. 2, vol. 3, p. 120。
關於積分又如何呢?在本書中我們已經多次見過,數學家們一度認為
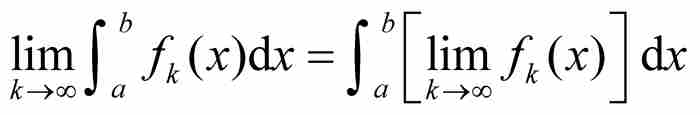
從這個等式斷定,我們可以萬無一失地交換兩種重要的微積分運算:先積分然後取極限,或者先取極限然後積分。
為了看出這同樣是錯誤的,我們在區間[0, 1]上定義一個由函數
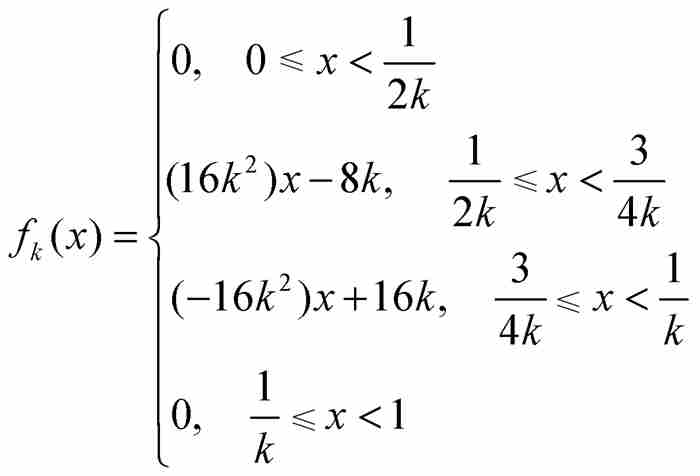
表示的序列 。這個函數表達式儘管看起來也許令人生畏,不過圖9-4中的f1,f2和f3的圖形顯示,這些函數是非常平常的。每個fk(x) 都是連續函數,它們的「尖峰」在越來越靠近原點的區域上變得越來越高,但寬度越來越小。
。這個函數表達式儘管看起來也許令人生畏,不過圖9-4中的f1,f2和f3的圖形顯示,這些函數是非常平常的。每個fk(x) 都是連續函數,它們的「尖峰」在越來越靠近原點的區域上變得越來越高,但寬度越來越小。
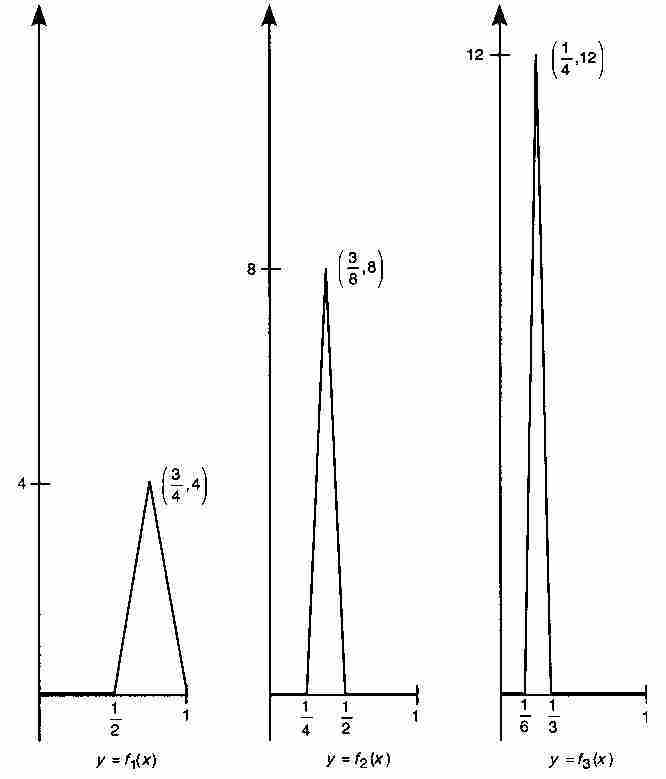
圖 9-4
由於fk是連續函數,對它們可以求積分,而它們的積分作為圖9-5中的三角形的面積是很容易計算的:
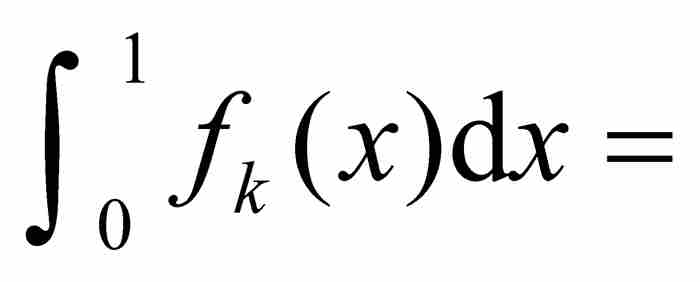 三角形面積
三角形面積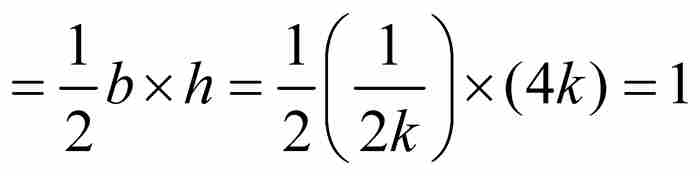
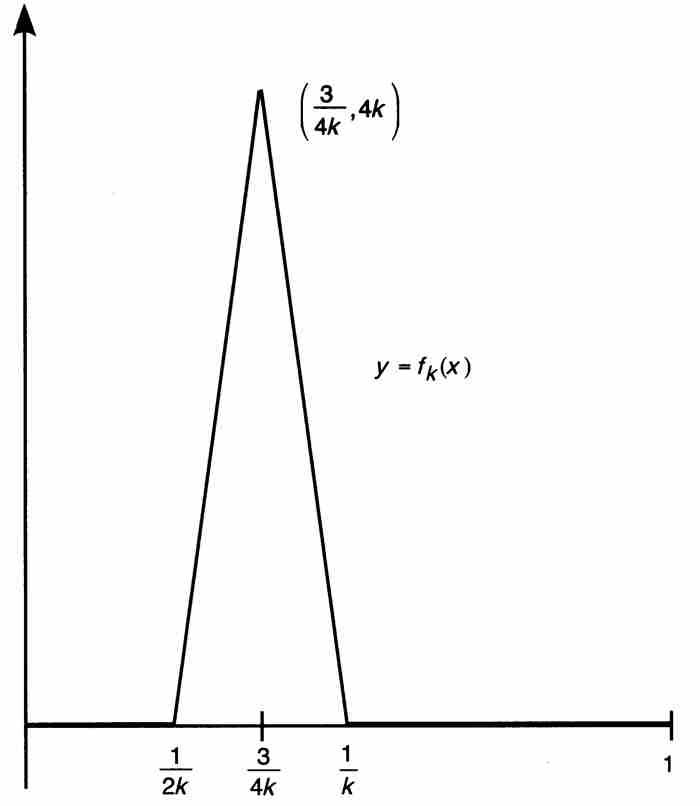
圖 9-5
所以,當這些三角形區域的底邊變得越來越小時,它們的高以三角形的面積保持不變這樣一種方式增加。於是,顯然有
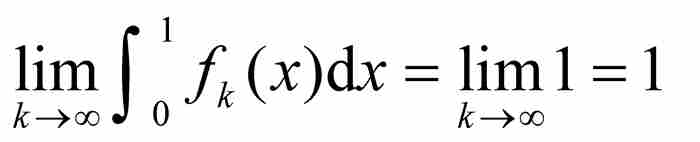 (2)
(2)
另一方面,我們斷言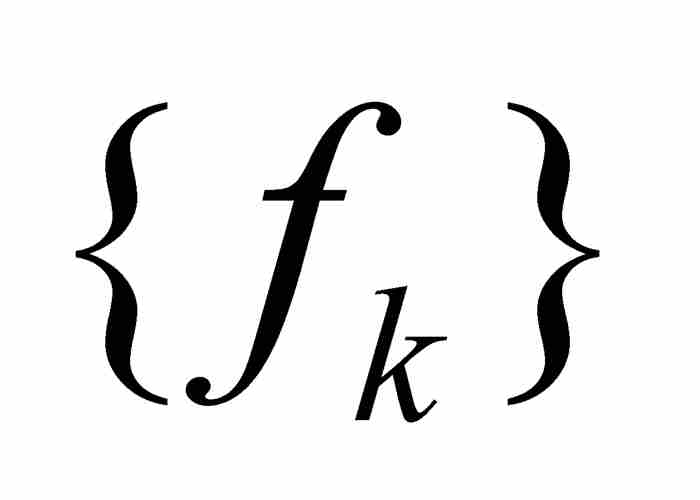 的點態極限在區間[0, 1]上處處為零。毫無疑問,
的點態極限在區間[0, 1]上處處為零。毫無疑問,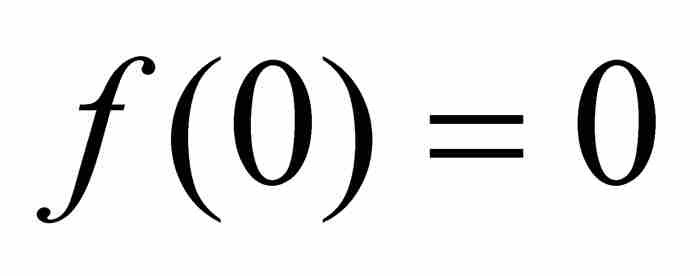 ,因為對於每個k有
,因為對於每個k有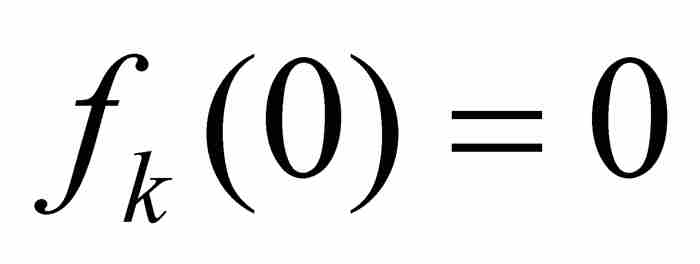 。同時,如果
。同時,如果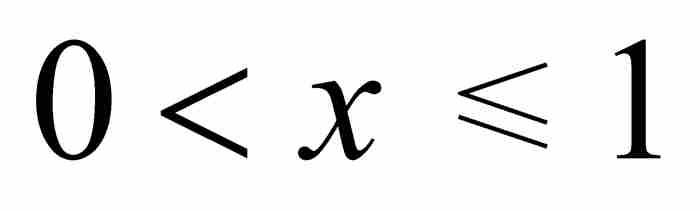 ,我們選擇一個滿足
,我們選擇一個滿足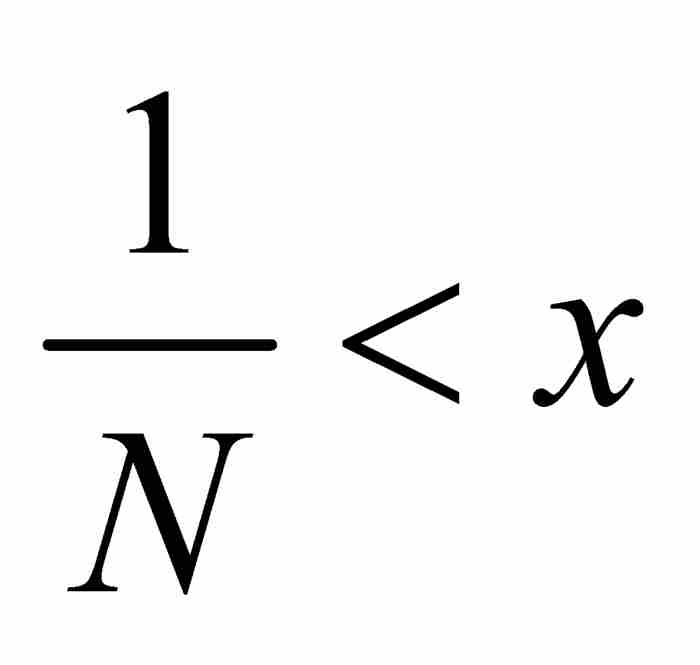 的自然數N,並且考察所有位於其後的函數,即所有滿足k≥N的fk,其「尖峰」已經移動到x的左側,致使
的自然數N,並且考察所有位於其後的函數,即所有滿足k≥N的fk,其「尖峰」已經移動到x的左側,致使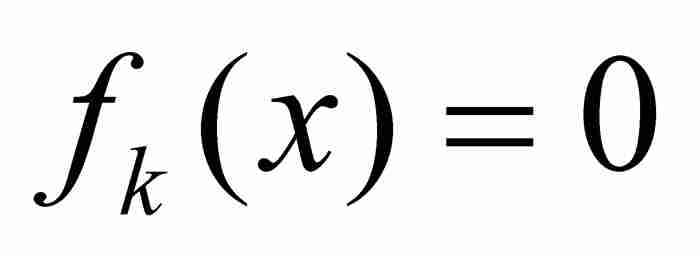 。因此也有
。因此也有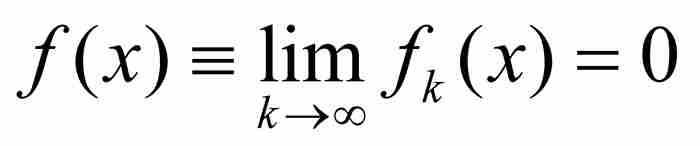 。我們由此看出
。我們由此看出
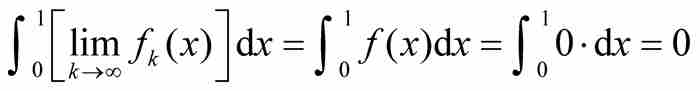
把這個結果同式(2)比較,就顯現令人沮喪的事實:函數序列積分的極限不一定等於極限函數的積分。用符號表示,我們得到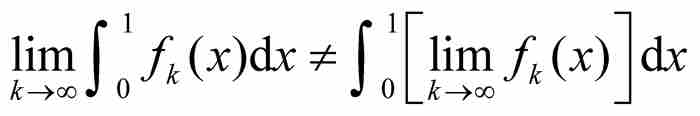 。再次看到,這個函數序列的點態極限不具備一種「優美的」解析特性,這是頗為遺憾的。
。再次看到,這個函數序列的點態極限不具備一種「優美的」解析特性,這是頗為遺憾的。
魏爾斯特拉斯在1841年之前就察覺到這種情況,並且提出一種解決方法。3 但是,以他固有的與眾不同的方式,他直到1894年才把自己的思想公諸於世,這已是在半個世紀之後的事情——好在他的學生們很早以前就把這種思想傳播出去了。他的想法是引進一種更強的收斂形式,稱為一致收斂,在這種收斂概念下,函數序列中個體函數的主要性質將會傳遞給它的極限函數。
3 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, p. 22。
倣傚他的做法,我們給出一致收斂的下述定義:倘若對於每個ε > 0,存在一個自然數N,如果k≥N而x為定義域中的任意點,那麼有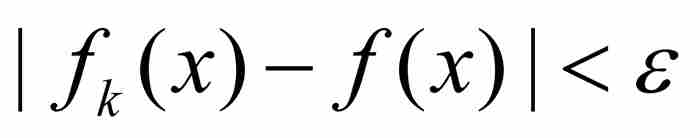 ,這時就說函數序列
,這時就說函數序列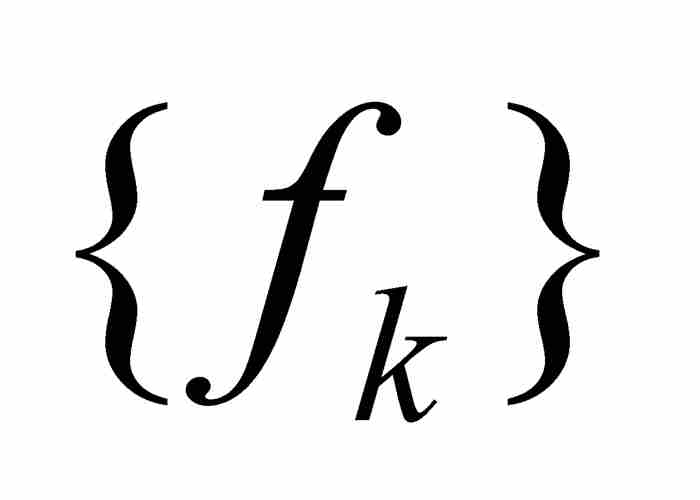 在共同定義域上一致收斂於函數f。聯想到一致連續性,這表明在函數
在共同定義域上一致收斂於函數f。聯想到一致連續性,這表明在函數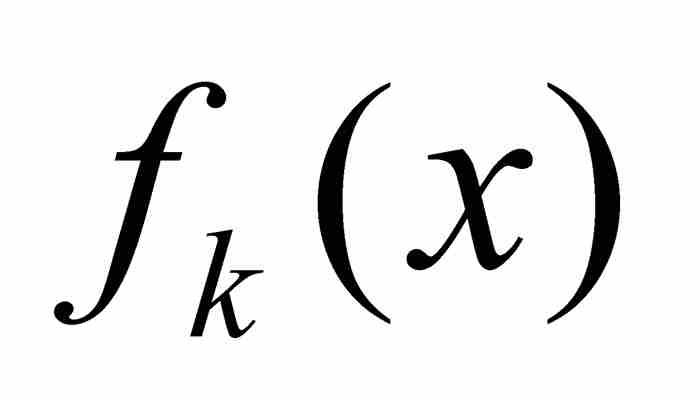 的定義域內「一個N適合於一切x」。
的定義域內「一個N適合於一切x」。
對於這種收斂方式,可以作出幾何解釋。給定ε > 0,我們畫一條包圍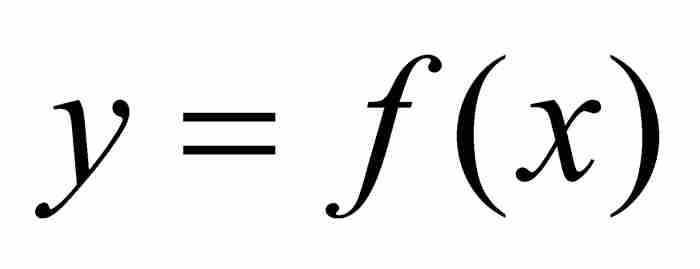 圖形的寬度為ε的帶狀區域,如圖9-6所示。依據一致收斂,我們必定達到這樣一個下標N,致使序列
圖形的寬度為ε的帶狀區域,如圖9-6所示。依據一致收斂,我們必定達到這樣一個下標N,致使序列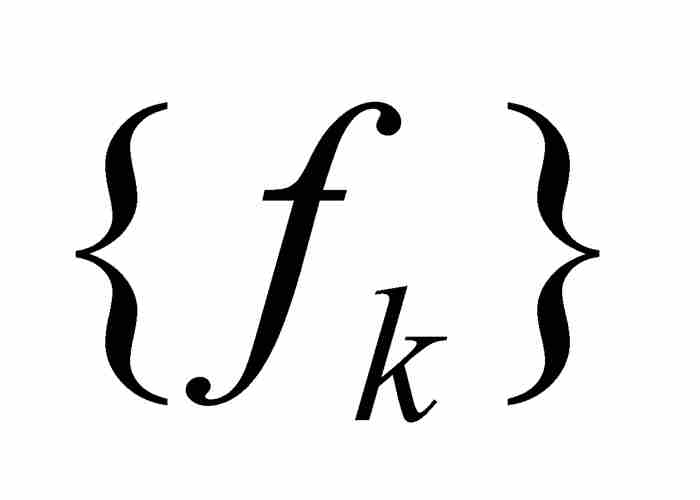 中的fN以及其後的所有函數全部落入這個帶狀區域。正如一致收斂這個名稱所顯示的,這樣一些函數在區間[a, b]上一致逼近f。
中的fN以及其後的所有函數全部落入這個帶狀區域。正如一致收斂這個名稱所顯示的,這樣一些函數在區間[a, b]上一致逼近f。
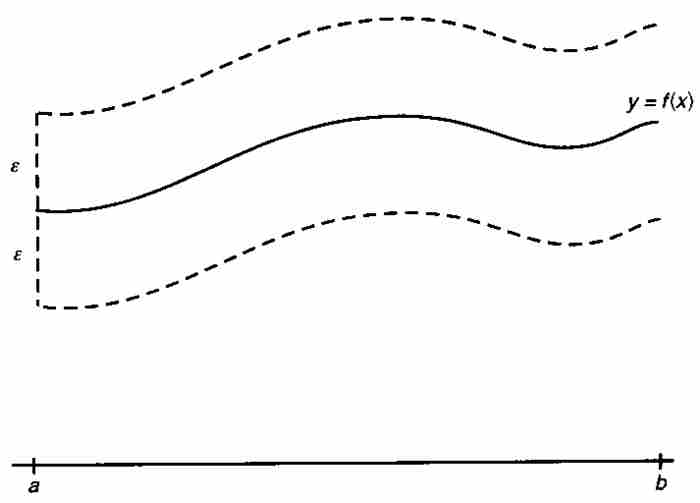
圖 9-6
不難看出,如果一個函數序列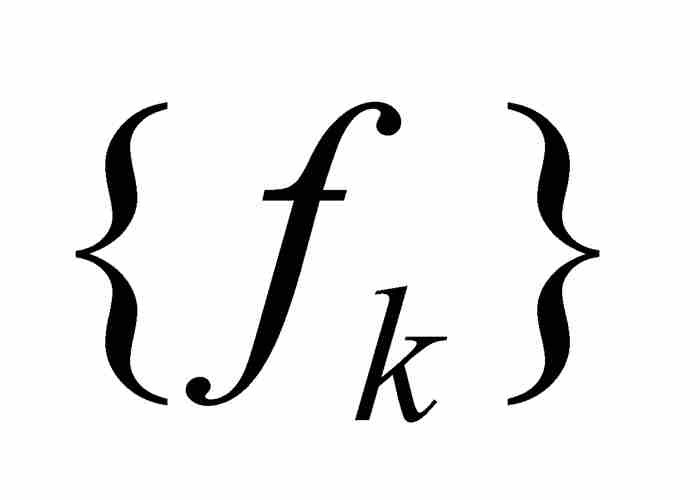 一致收斂於函數f,那麼
一致收斂於函數f,那麼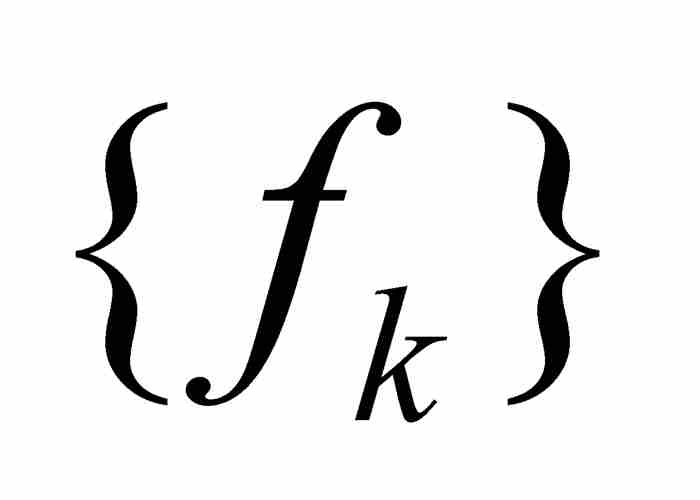 點態收斂於f,但是相反的命題不成立。例如,前面描述的「尖峰」函數序列在區間[0, 1]上點態收斂於零值函數,但是不一致收斂於零值函數。同僅僅是點態收斂相比,一致收斂算是一種更強的和限制更大的收斂形態。
點態收斂於f,但是相反的命題不成立。例如,前面描述的「尖峰」函數序列在區間[0, 1]上點態收斂於零值函數,但是不一致收斂於零值函數。同僅僅是點態收斂相比,一致收斂算是一種更強的和限制更大的收斂形態。
出於幾點原因,我們在這裡脫離了主題。首先,在本章的主要結果中需要用到一致收斂的概念。其次,這些思想在本書其餘部分反覆出現。最後,這樣一些成熟的見解足以說明,在微積分的歷史上魏爾斯特拉斯何以佔有如此重要的地位。Victor Katz對於他的工作作出這樣的評價:
在魏爾斯特拉斯給出的定義中,他不僅絕對清楚某些量是如何依賴於其他量的,而且完成了不用像「無窮小」這樣一些術語的轉變。從此以後,凡是涉及這類概念的定義,全部都是用算術方式給出的。4
4 Victor Katz, A History of Mathematics: An Introduction, Harper-Collins, 1993, p. 657。
四個重要定理
魏爾斯特拉斯不僅重新審視分析學中的各種定義,同時他還是應用它們證明重要定理的大師。下面我們給出他獲得的四個涉及一致收斂的結果,不過不予證明。
前面兩個定理解決上面提及的一個題目:在一致收斂條件下,函數的重要的解析性質從函數序列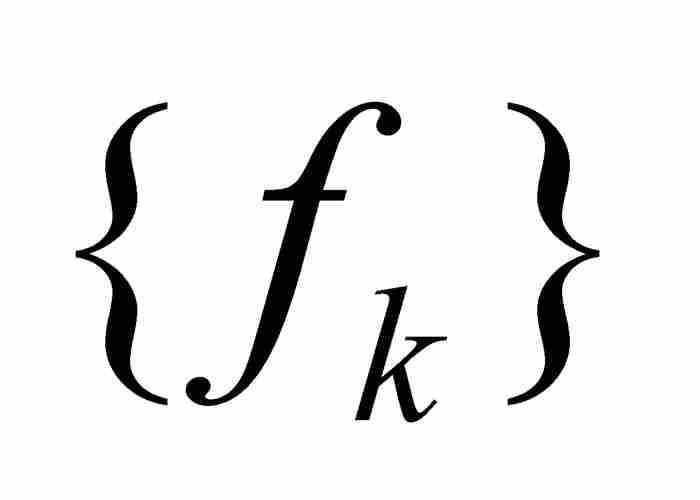 的個體項傳遞給它們的極限函數f。
的個體項傳遞給它們的極限函數f。
定理 1 如果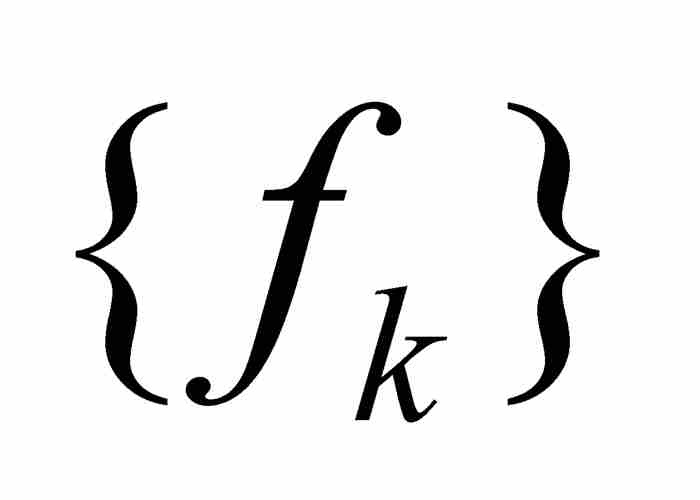 是在區間[a, b]上一致收斂於f的連續函數的序列,那麼f本身也是連續函數。
是在區間[a, b]上一致收斂於f的連續函數的序列,那麼f本身也是連續函數。
定理 2 如果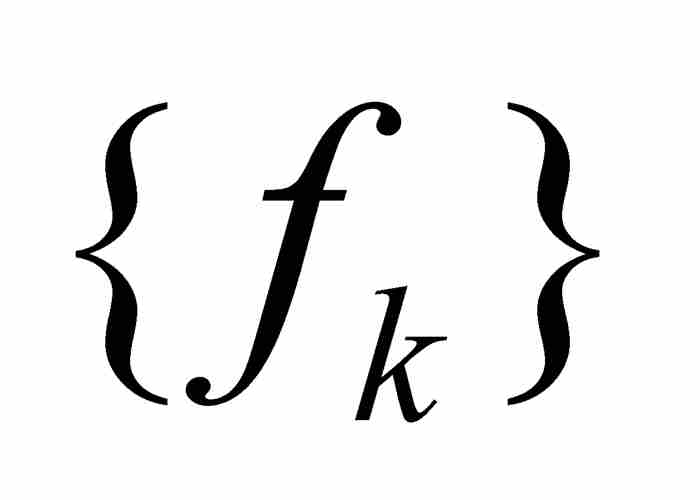 是在區間[a , b]上一致收斂於f的有界黎曼可積函數的序列,那麼f在[a, b]上是黎曼可積的,並且
是在區間[a , b]上一致收斂於f的有界黎曼可積函數的序列,那麼f在[a, b]上是黎曼可積的,並且
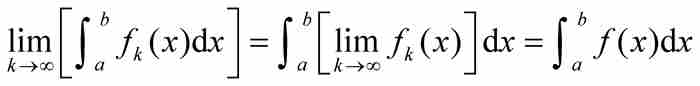
根據定理2,對於一致收斂的函數序列,允許進行取極限與求積分的交換。
第三個定理如今稱為魏爾斯特拉斯逼近定理。這個定理在連續函數同多項式之間提供一種始料未及的聯繫。
定理 3(魏爾斯特拉斯逼近定理) 如果f是定義在有界閉區間[a, b]上的連續函數,那麼存在一個在[a, b]上一致收斂於f的多項式的序列{Pk}。
這個定理如此令人著迷,原因在於有的連續函數可能是特性極差的(事實上,這正是我們馬上要考察的魏爾斯特拉斯反例的特點)。相比之下,多項式卻是非常平和的函數。後者竟然可能一致逼近前者,這彷彿是一樁奇妙的天賜良緣。
這三個定理都與一致收斂有關。它們使連續性和可積性從函數序列的個體函數傳遞給它們的極限函數,並且提供一種用多項式逼近連續函數的手段。但是首先要問,存在確定一致收斂的簡單方法嗎?
判別一致收斂的一種途徑是用所謂的魏爾斯特拉斯M檢驗法,這是我們初步結果中的最後一個定理。像前面那樣,我們從在一個共同定義域上定義的函數序列{ fk}開始,不過M檢驗法引進一種新奇的方法:我們把序列的前n項相加,建立部分和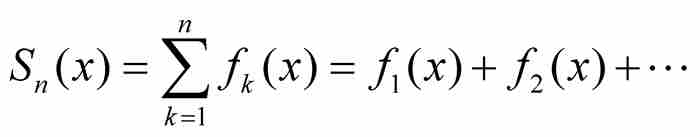
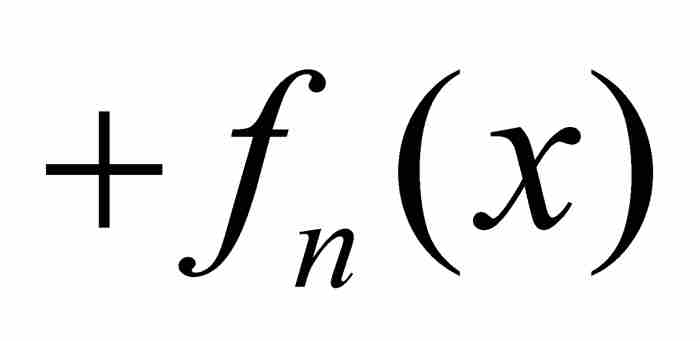 。如果部分和的序列{Sn}一致收斂於一個函數f,我們就說函數項的無窮級數
。如果部分和的序列{Sn}一致收斂於一個函數f,我們就說函數項的無窮級數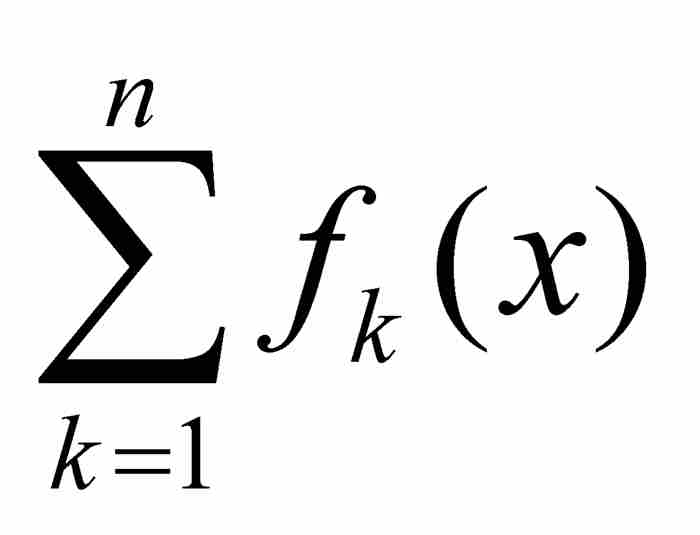 一致收斂於f (x)。在這個基礎上,現在我們來陳述下述結果。
一致收斂於f (x)。在這個基礎上,現在我們來陳述下述結果。
定理 4(魏爾斯特拉斯M檢驗法) 設{fk (x)}是定義在一個共同定義域上的函數序列。如果對於每個k,存在一個正數Mk,使得對於定義域內的所有x,有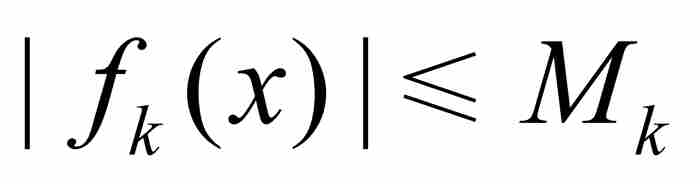 ,並且如果無窮級數
,並且如果無窮級數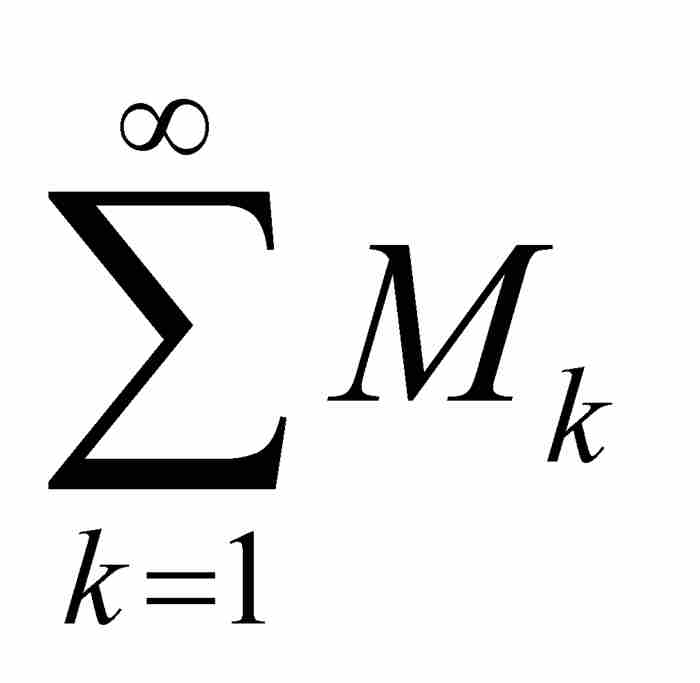 收斂,那麼函數項級數
收斂,那麼函數項級數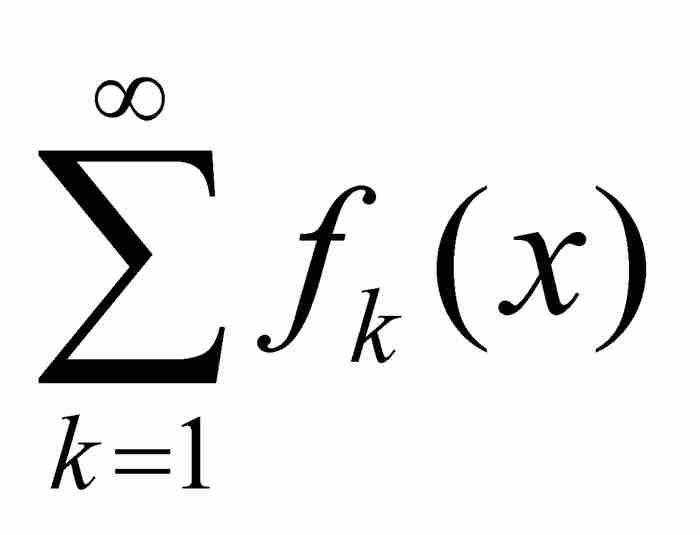 一致收斂。
一致收斂。
這個檢驗法相當於函數級數與數值級數之間的一個比較檢驗法,其中數值級數的收斂蘊含函數級數的一致收斂。例如,考慮區間[0,1]上由
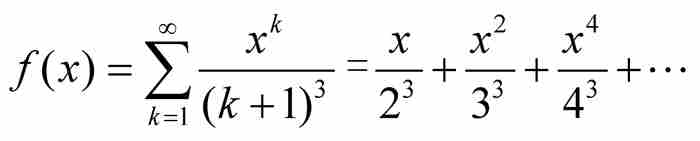
定義的函數。這裡,對於[0, 1]內的所有x,我們有| fk(x)|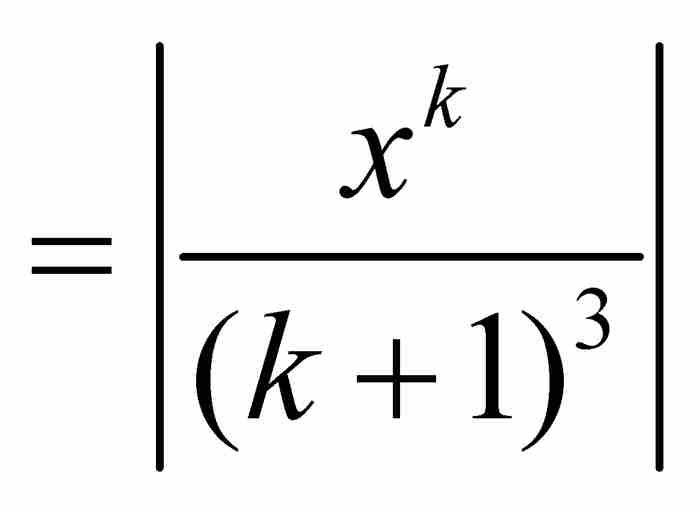
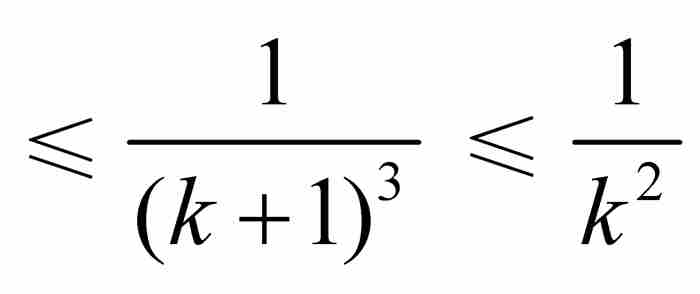 ,而根據第4章歐拉關於雅各布·伯努利難題的結果,可知
,而根據第4章歐拉關於雅各布·伯努利難題的結果,可知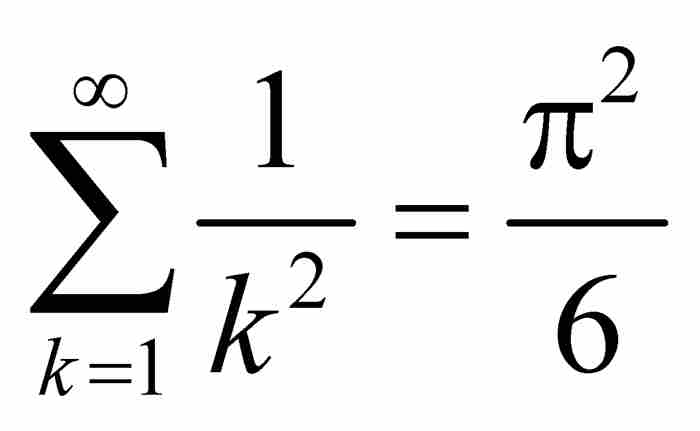 。由M檢驗法立即推出函數f (x) 一致收斂。此外,如果對部分和Sn(x)應用定理1和定理2,可知f本身也是連續函數,因為每個部分和函數是連續的,並且
。由M檢驗法立即推出函數f (x) 一致收斂。此外,如果對部分和Sn(x)應用定理1和定理2,可知f本身也是連續函數,因為每個部分和函數是連續的,並且
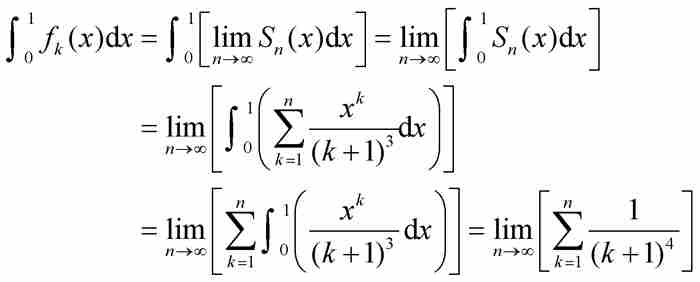
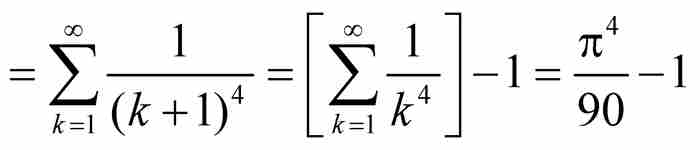
其中再次得益於歐拉關於級數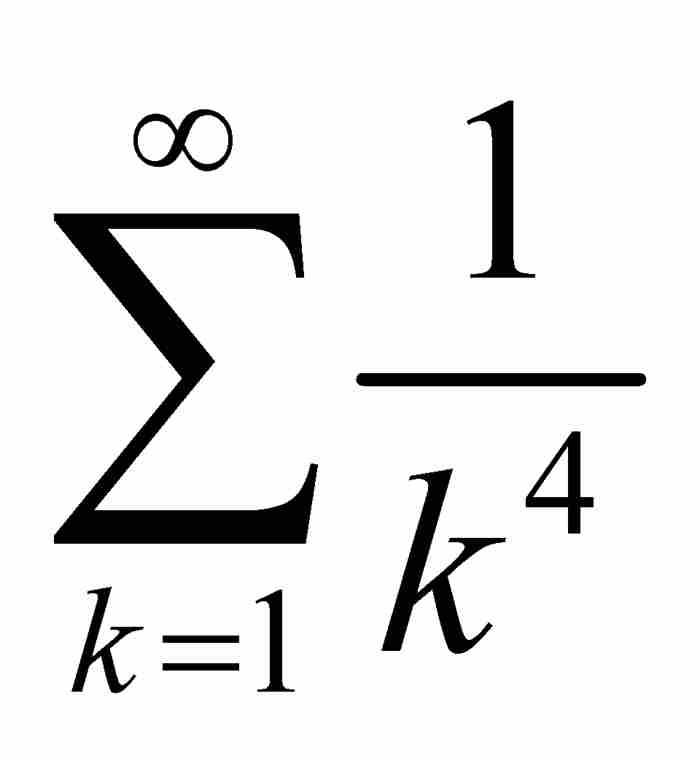 的結果。至此,對於交換取極限與求積分的無限過程,無論情況多麼複雜,我們已經提示所有的干預步驟。魏爾斯特拉斯M檢驗法使我們能夠斷定f (x)是連續函數,並且準確地求出它的積分值,這是一個具有重大意義的成就。
的結果。至此,對於交換取極限與求積分的無限過程,無論情況多麼複雜,我們已經提示所有的干預步驟。魏爾斯特拉斯M檢驗法使我們能夠斷定f (x)是連續函數,並且準確地求出它的積分值,這是一個具有重大意義的成就。
我們終於完成了一切準備工作,搭建起數學史上行將演繹的一個轟動事件的舞台。
魏爾斯特拉斯病態函數
數學家們早就知道,一個可微的(「光滑的」)函數必定是連續的(「不間斷的」)函數,但是,反之不然。例如,一個像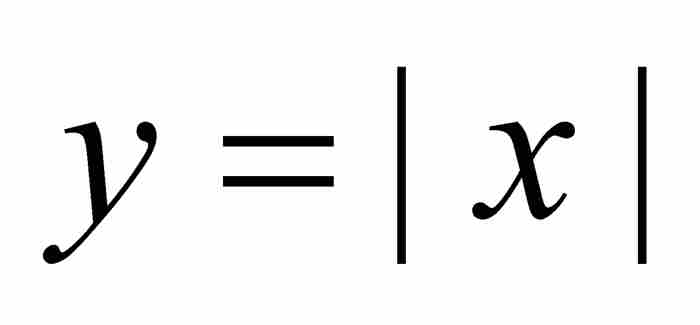 這樣的V字型函數是處處連續的函數,但是它在x = 0處是不可微的,它的圖形在那裡突然改變方向,形成一個拐角。
這樣的V字型函數是處處連續的函數,但是它在x = 0處是不可微的,它的圖形在那裡突然改變方向,形成一個拐角。
然而,人們曾經認為連續函數必定「多半」是光滑的。赫赫有名的安德烈·馬裡·安培(1775—1836)對連續函數通常是可微的命題曾經提出過一個證明,而且在19世紀整個前半期,微積分學教科書都支持這種見解。1
1 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, pp. 43-44。
這無疑是有吸引力的。任何人可以想像這樣一幅連續的「鋸齒」狀圖形,平滑地上升到一個齒角,然後下降到下一個齒角,接著再上升到另一個齒角,如此延續下去。當我們壓縮「鋸齒」時,得到越來越多不可微的點。儘管如此,似乎必定繼續存在使函數圖形從一個齒角平滑地上升或者下降到另一個齒角的區間。由此可見,幾何圖形表明,任何連續函數必定存在大量可微的點。
因此,當魏爾斯特拉斯構造出處處連續但是無處可微的函數時,引起巨大震驚,這是一個稀奇古怪的函數實體,它看起來是連續的,卻是處處參差不齊的。這個函數被大多數人視為難以想像的,它不僅推翻了安培的「定理」,而且把幾何直觀作為微積分的可靠基礎的主張逐出了歷史舞台。
人們普遍認為,魏爾斯特拉斯是在19世紀60年代構造出他的例子的,並且在1872年7月18日把這個例子提交給柏林科學院。按照以往的習慣,魏爾斯特拉斯沒有匆忙公佈他的發現;直到1875年,這個病態函數才由保羅·杜布瓦·雷蒙(1831—1889)首次發表。
毋庸置疑,一個如此特殊的函數自然遠非初等函數。就其學術上的複雜程序而言,它或許是本書中要求最苛刻的結果。但是,由於這個函數獨具的違反直覺的特性,努力構造它是非常值得的,更不用說它具有的歷史意義了。下面我們倣傚魏爾斯特拉斯的論證,但是改變了他的記號,同時為了清晰起見,間或添加了某些細節。
我們從一個引理開始,這個引理是魏爾斯特拉斯在證明中需要使用的。他用一個三角恆等式證明這個引理,但是我們給出利用微積分的一個證明。
引理 如果B > 0,那麼
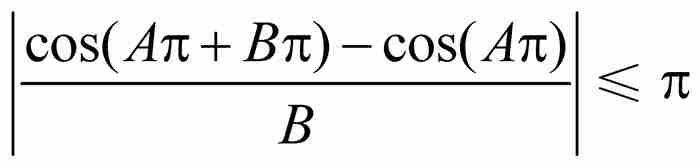
證明 令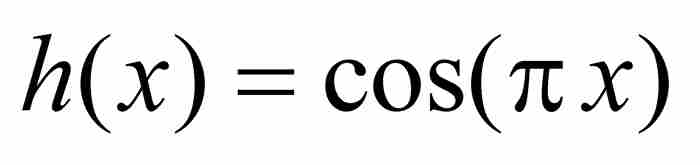 是區間[A, A + B]上的函數。根據中值定理,在A和A + B之間存在一點c,使得
是區間[A, A + B]上的函數。根據中值定理,在A和A + B之間存在一點c,使得
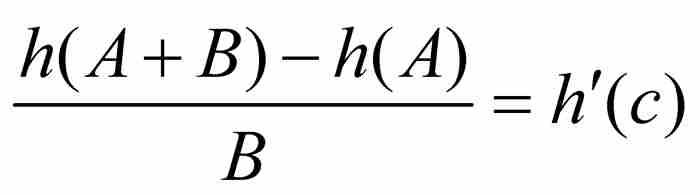
這個結果等價於
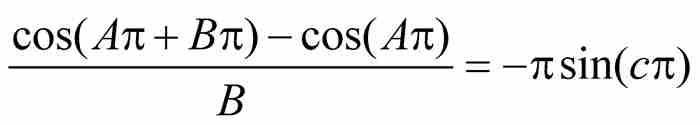
由此推出
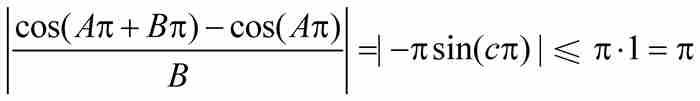
現在我們用魏爾斯特拉斯本人當初的表達方式介紹他的著名反例。
定理 如果 a ≥ 3 是一個奇數,b是嚴格介於0與1之間的一個常數且滿足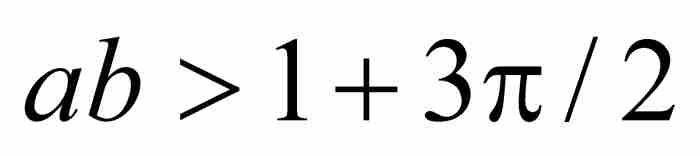 ,那麼函數
,那麼函數
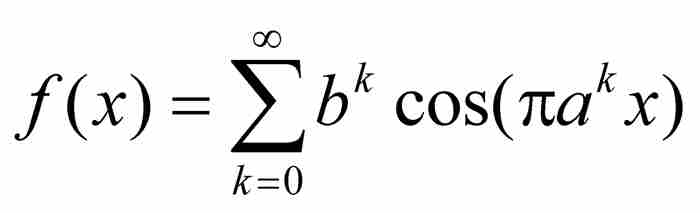
是處處連續的和無處可微的。2
2 Karl Weierstrass, Mathematische Werke, vol. 2, Berlin, 1895, pp. 71-74。

魏爾斯特拉斯病態函數(1872)
證明 顯然,魏爾斯特拉斯在對a和b設置這些離奇的約束條件之前,已經進行了大量收集材料的準備工作。為了簡化討論,我們將取a = 21和b = 1/3。這種選擇滿足定理中設定的條件,因為 a ≥ 3 是一個奇數,b位於區間(0, 1)內,並且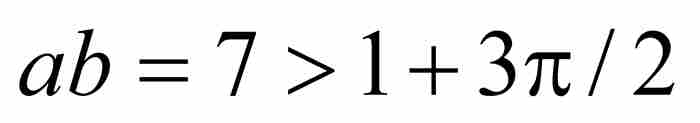 。所以,我們的特定函數將是
。所以,我們的特定函數將是
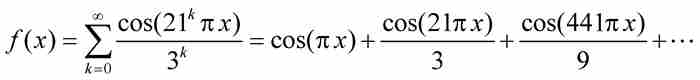 (3)
(3)
為了證明f的連續性,只需應用M檢驗法。顯而易見,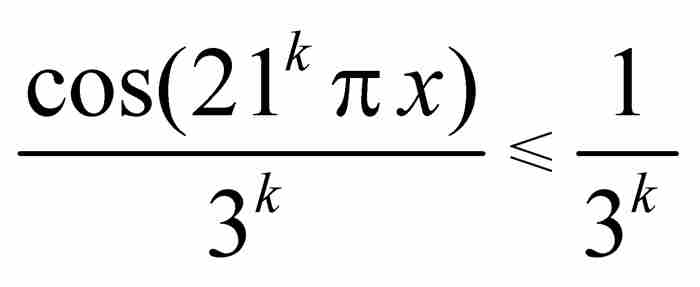 ,而
,而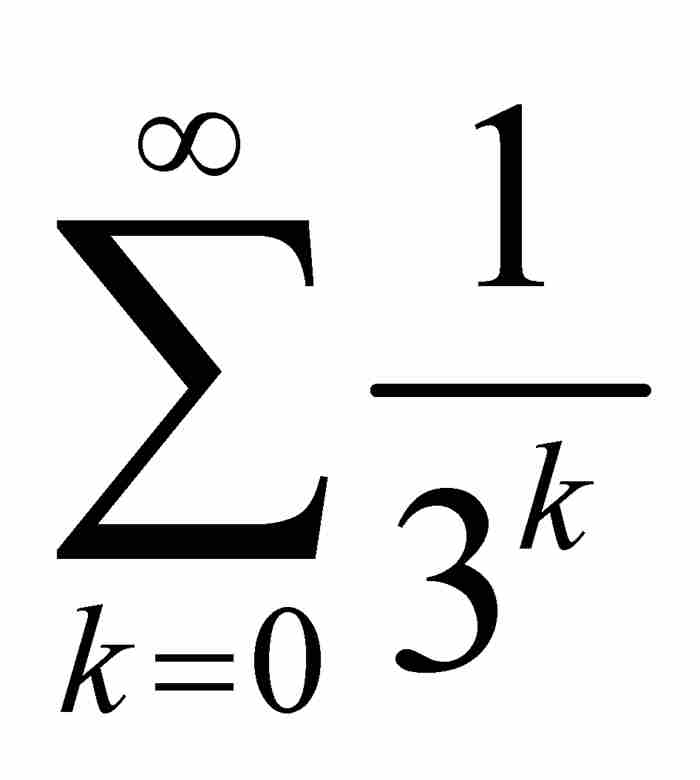 收斂於3/2。因此,這個級數一致收斂於f。由於每個直和項
收斂於3/2。因此,這個級數一致收斂於f。由於每個直和項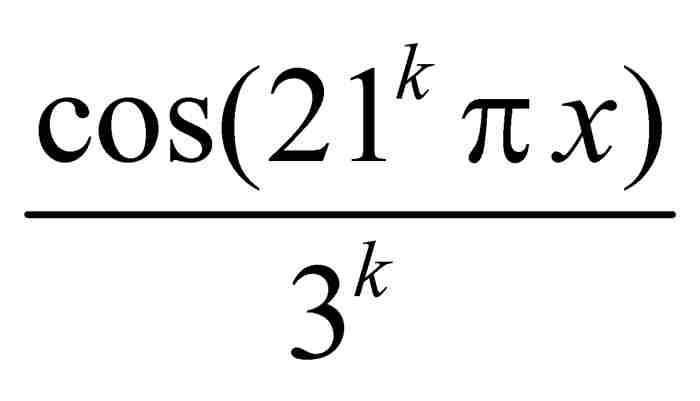 是處處連續的,所以根據前面的定理1,f也是處處連續的。
是處處連續的,所以根據前面的定理1,f也是處處連續的。
對於證明函數f是處處連續的和無處可微的,看起來我們已做了一半工作,然而,證明它是「無處可微的」部分卻是難上加難的。為此目的,我們從固定一個實數r開始。我們的目標在於證明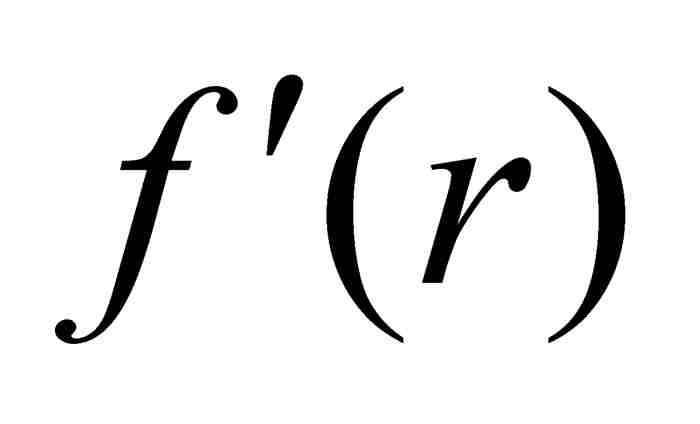 是不存在的。由於r是任意的,這個結果也就證實f無論在什麼點都是不可微的。
是不存在的。由於r是任意的,這個結果也就證實f無論在什麼點都是不可微的。
在下述魏爾斯特拉斯推理中,彙集一些看上去沒有聯繫的問題的若干結果是有益的。毫無疑問,其中每個結果都會在他的盛大演出的某個場合扮演重要角色。
首先,魏爾斯特拉斯注意到,對於每個m = 1, 2, 3, …,實數21 mr(像任何實數一樣)處於同它最接近的整數的半個單位的範圍內。因此,對於每個整數m,存在這樣一個整數αm,使得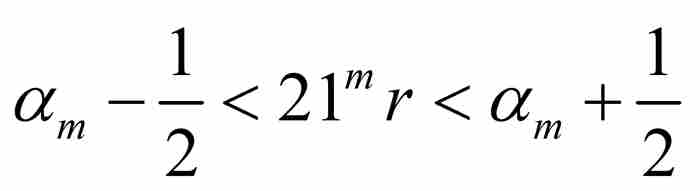 (參見圖9-7)。令
(參見圖9-7)。令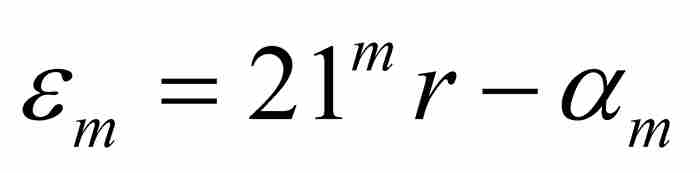 為
為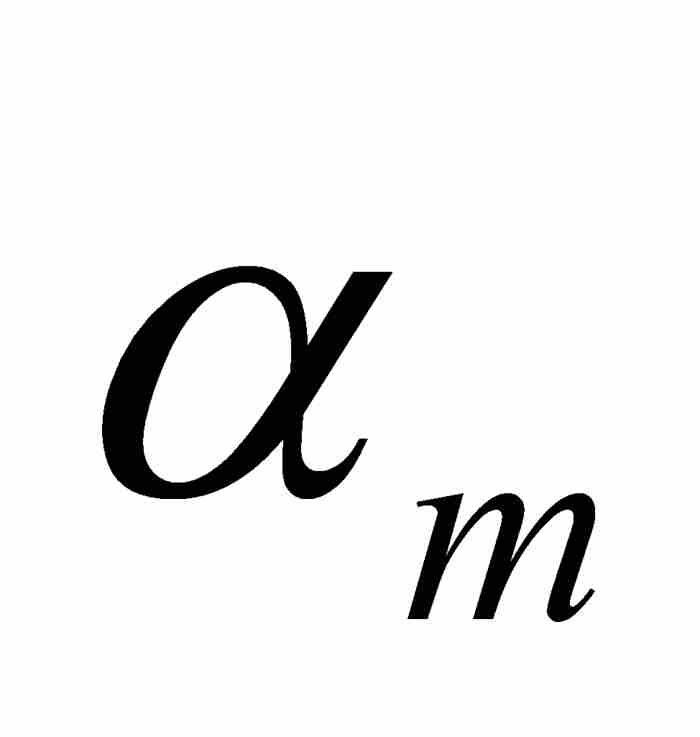 同21 mr之間的間距,我們看出
同21 mr之間的間距,我們看出
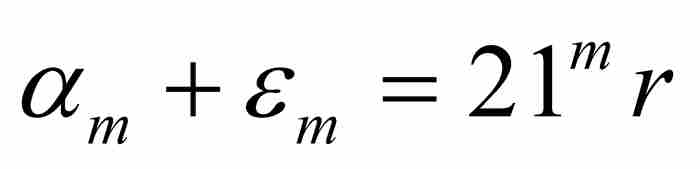 (4)
(4)

圖 9-7
由於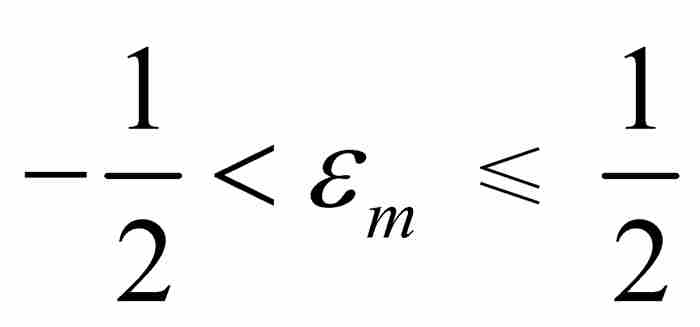 ,所以
,所以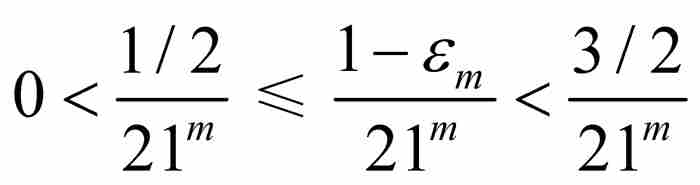 。為了便於表示,我們引入
。為了便於表示,我們引入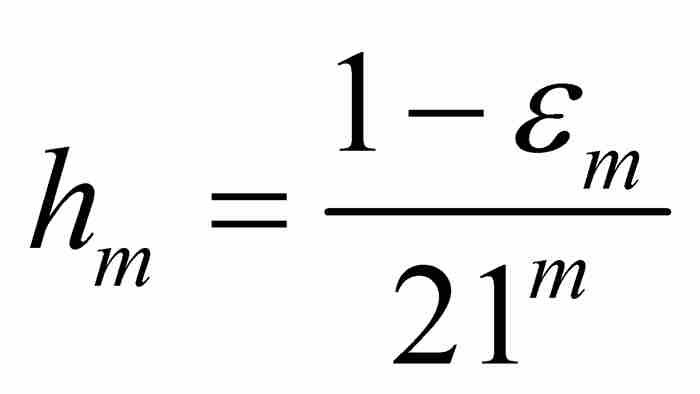 ,並且注意
,並且注意
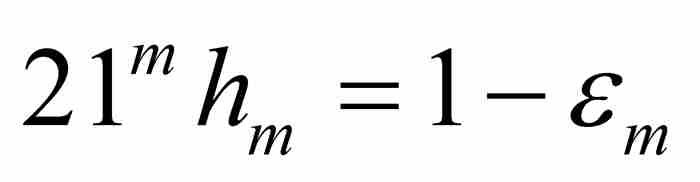 和
和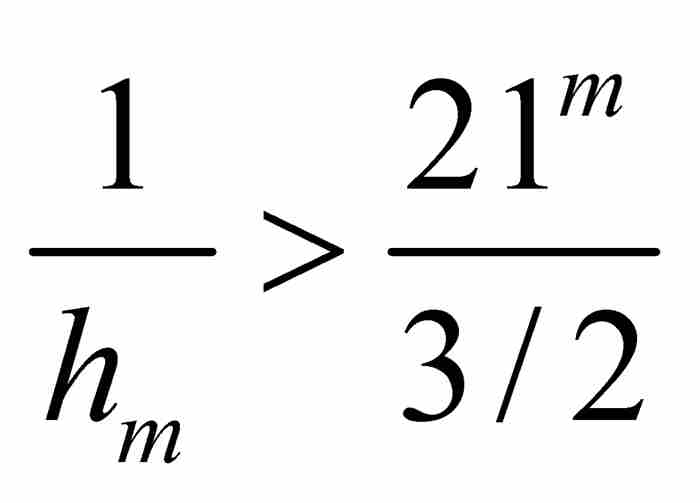 (5)
(5)
現在,根據擠壓定理,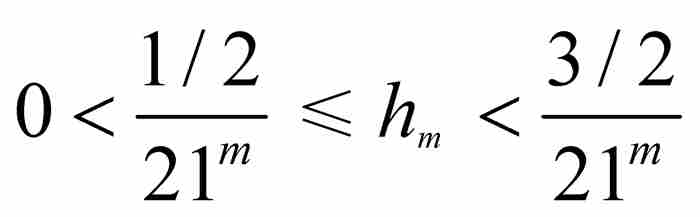 足以保證
足以保證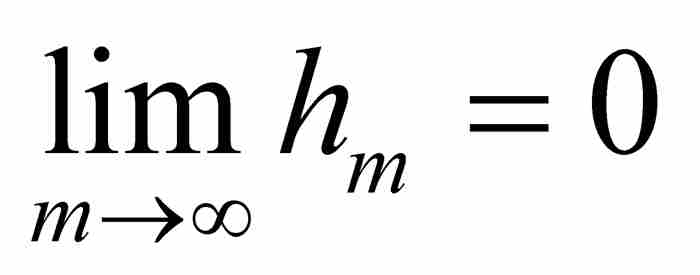 。這個正數項序列將在證實f (x)的不可微性中起決定性作用。
。這個正數項序列將在證實f (x)的不可微性中起決定性作用。
這時,我們(暫且)固定整數m。像魏爾斯特拉斯所做的那樣,我們利用式(3),並且考察微商:
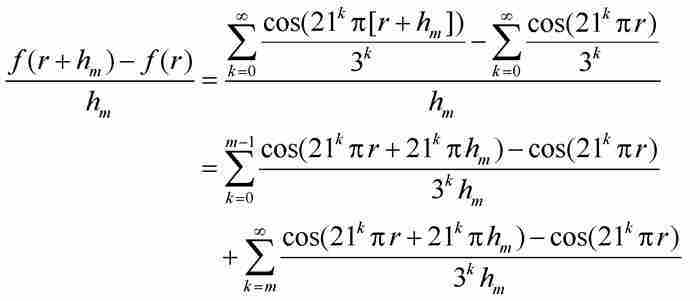
(6)
在此,無窮級數已經被分成兩部分。魏爾斯特拉斯將分別考察每一部分的絕對值。
對於第一個級數,我們應用引理,並取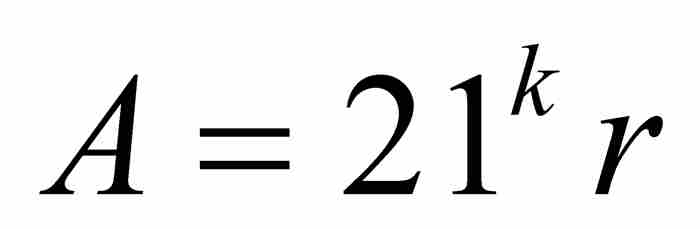 和
和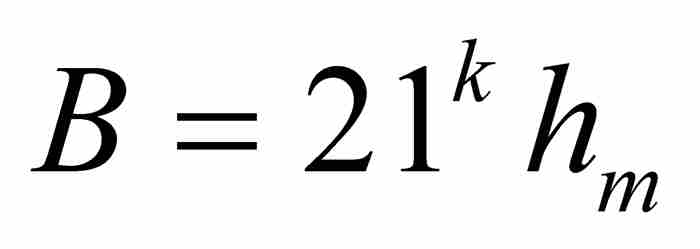 ,確定每個直和項的界如下:
,確定每個直和項的界如下:
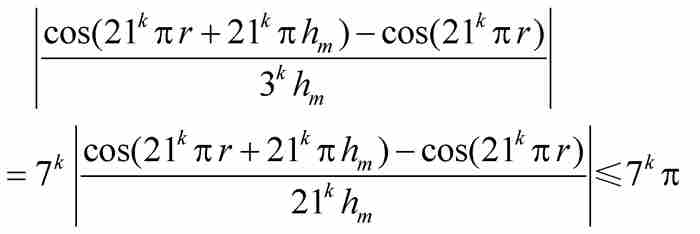
於是,由三角不等式,我們得到第一個級數的一個上界:
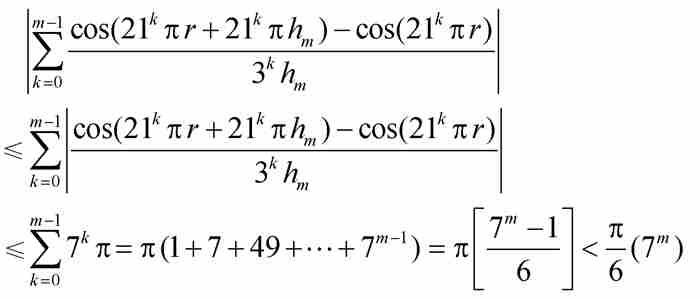
(7)
式(6)中的第二個級數提出一個更大的挑戰。為了確定它的絕對值,我們進行四項相關的考察:
(A)如果k≥m,由式(4)和式(5)看出
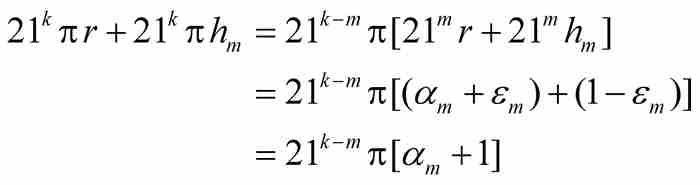
但是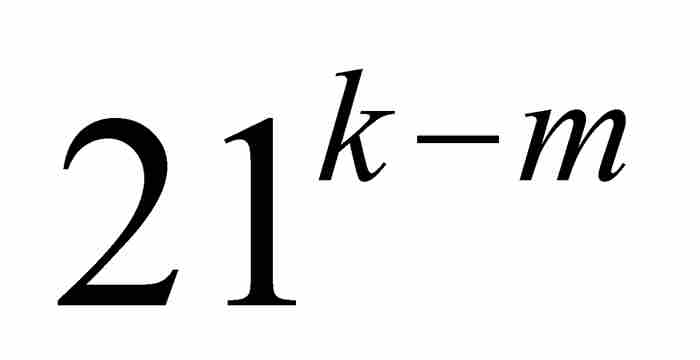 是一個奇數,而αm也是一個整數。因此,
是一個奇數,而αm也是一個整數。因此,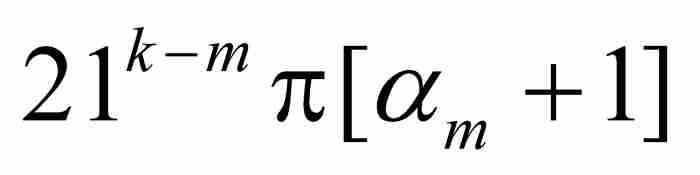 等於 π 的偶數倍或者奇數倍,這取決於
等於 π 的偶數倍或者奇數倍,這取決於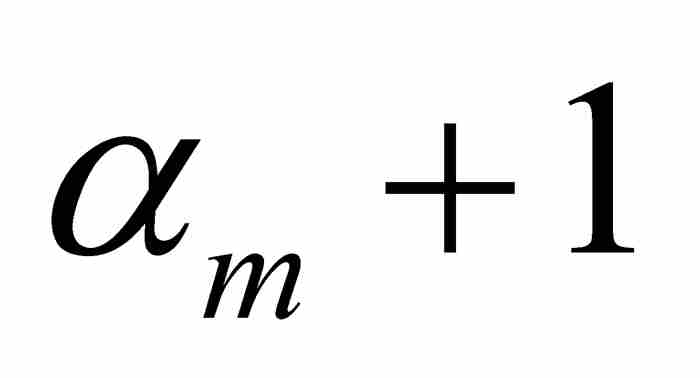 為偶數或者奇數。由此推出
為偶數或者奇數。由此推出
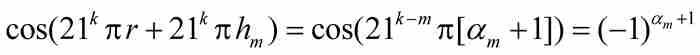
(B)我們再限定k≥m,並且利用式(4),得到
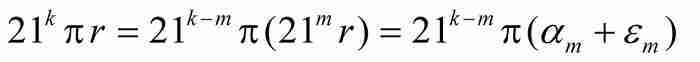
由一個眾所周知的三角恆等式,我們得到
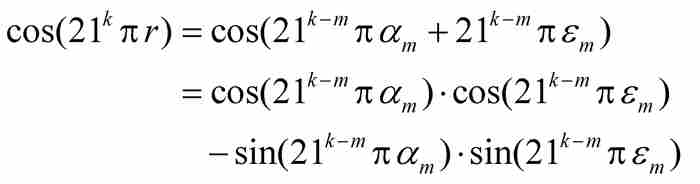
此處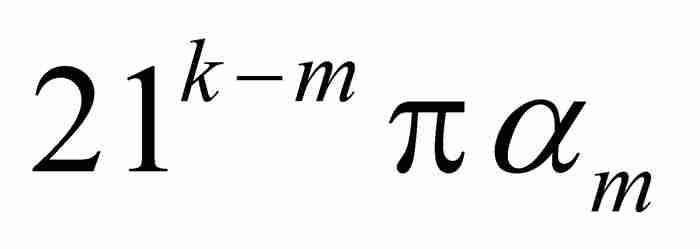 等於π的偶數倍或者奇數倍,這取決於
等於π的偶數倍或者奇數倍,這取決於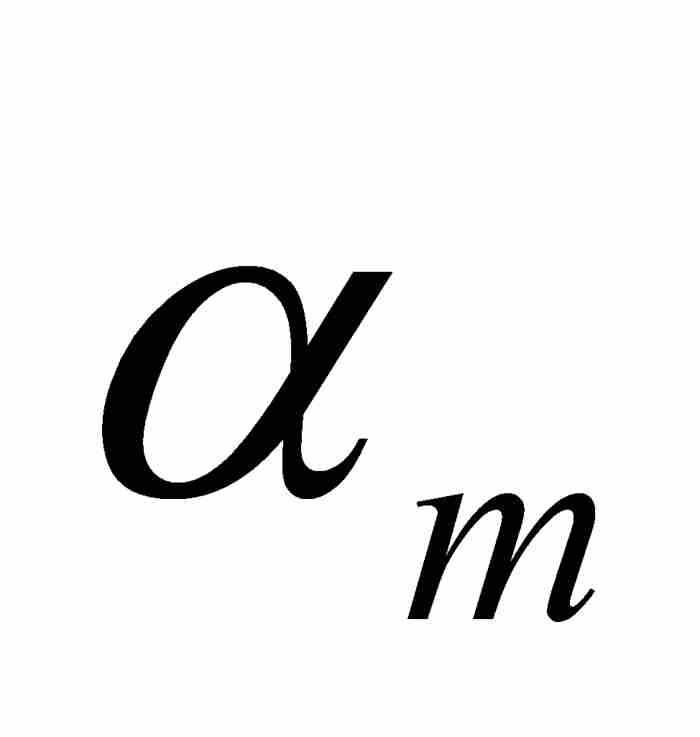 為偶數或者奇數,所以
為偶數或者奇數,所以
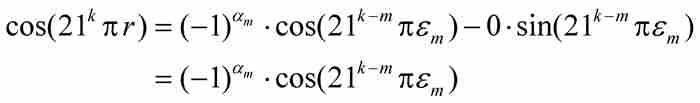
(C)(這是一項容易求得的結果)由於餘弦的性質,
(D)由於 ,可知
,可知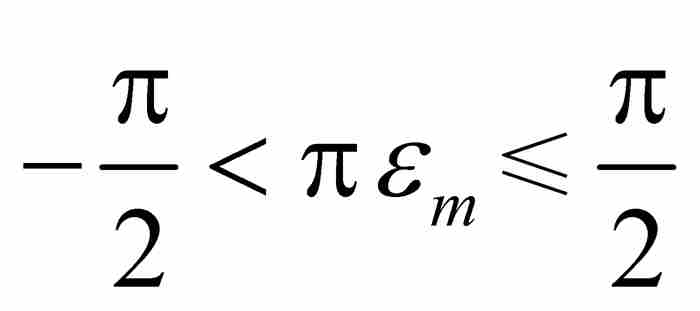 ,所以
,所以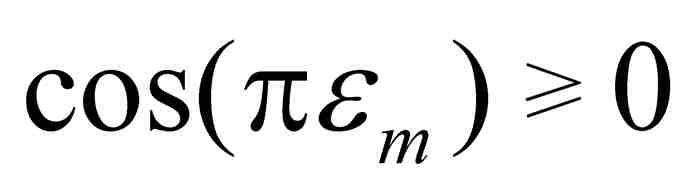 。
。
現在,對於式(6)中第二個級數應用(A)和(B)的結果,得到它的絕對值的一個下界:

最後一個等式成立是因為根據(C),級數中的每一項取非負值。
這個非負項級數的和必定大於它的第一項(其中k = m),所以根據(D)和式(5),我們得到
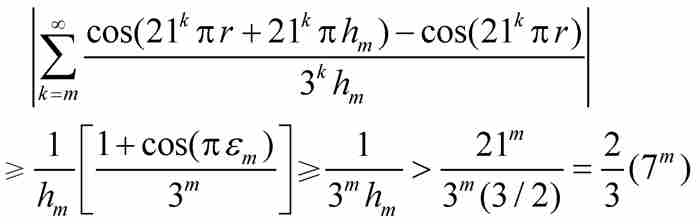
以上全部推導,落下了正劇之前的冗長序幕。魏爾斯特拉斯此時導出了關鍵性的不等式,他從剛才證明的結果開始,最終確定函數f (x)的微商的界限:
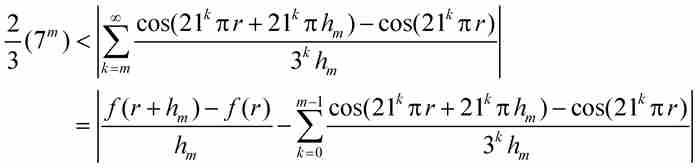
(根據式(6))
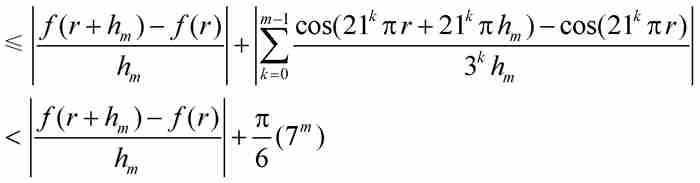
(根據式(7))
從這一串不等式中的第一個和最後一個,我們推出
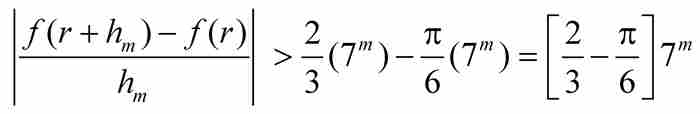 (8)
(8)
表達式(8)具有兩個主要特性:第一,數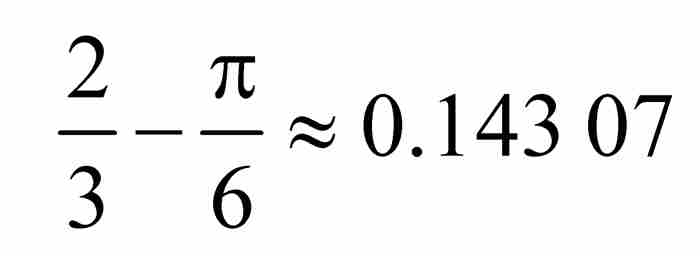 是一個正常數。第二,式(8)中的不等式對於我們所取的固定的自然數m成立,而m是隨意取的。考慮到這一點,我們現在「不固定」m,並且取極限:
是一個正常數。第二,式(8)中的不等式對於我們所取的固定的自然數m成立,而m是隨意取的。考慮到這一點,我們現在「不固定」m,並且取極限:
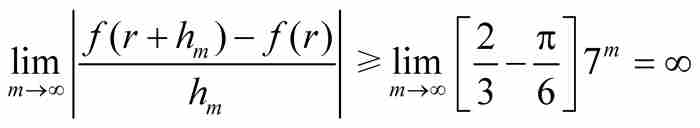
但是我們注意到,當 時
時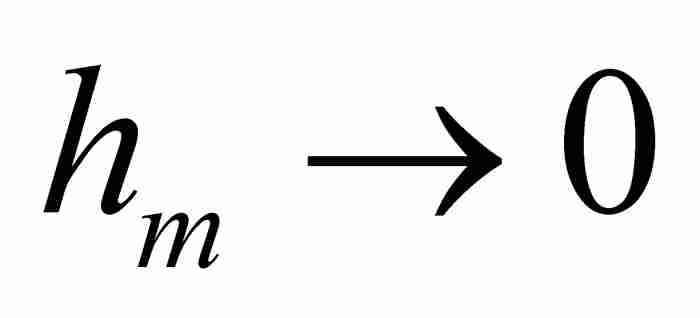 。因此,
。因此,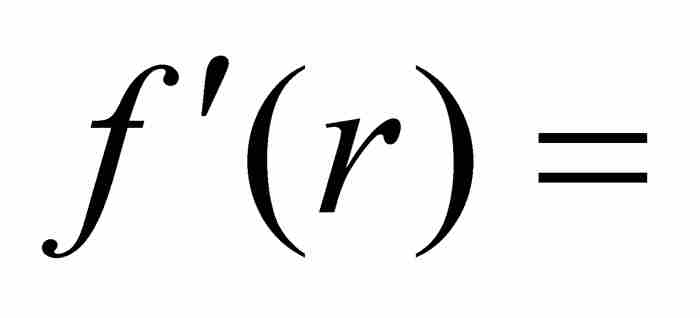
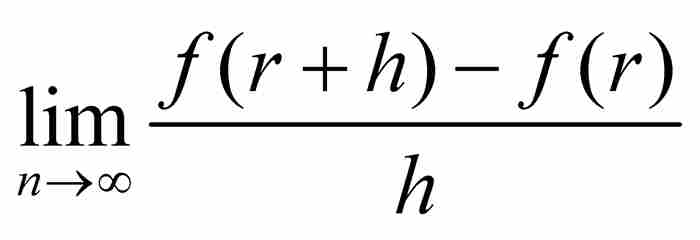 不能作為一個有限量存在。簡單地說(簡單嗎?)
不能作為一個有限量存在。簡單地說(簡單嗎?)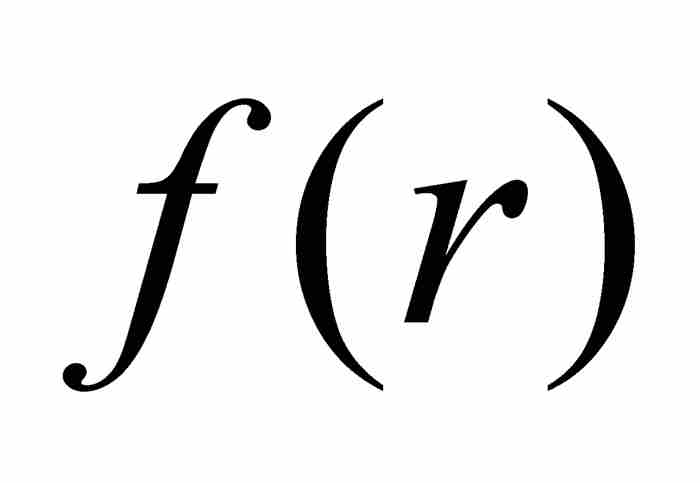 在x = r是不可微的。同時,由於r是一個未指定的實數,這就證實魏爾斯特拉斯定義的函數是無處可微的,儘管它是處處連續的函數。
在x = r是不可微的。同時,由於r是一個未指定的實數,這就證實魏爾斯特拉斯定義的函數是無處可微的,儘管它是處處連續的函數。
當讀者從魏爾斯特拉斯論證的震撼下恢復平靜時,多半會產生一些反應。反應之一會是對他所表現的才能萬分驚訝。他在整合這個證明中顯示出的天賦是出類拔萃的。
另一個反應是可能產生某種不安的感覺,因為我們恰好證實了一個連續函數可以不存在可微性點。函數的圖形無處是平滑地上升的或者下降的。在它的圖形上沒有一點存在一條切線。這是一個離奇的函數,它的每個點好似一個尖角,然而它又是處處連續的。
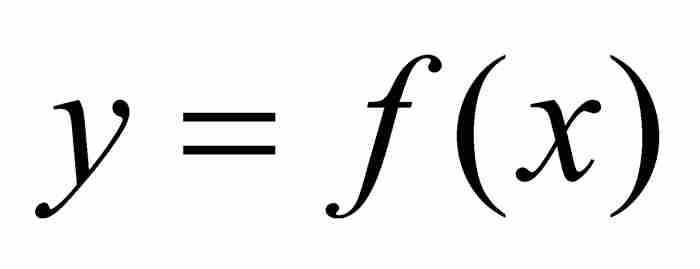 的圖形是否會給我們一些啟發呢?很遺憾,由於f是函數項的一個無窮級數,我們只能停留於畫出部分函數和的圖形。例如,我們在圖9-8中僅畫出第3個部分和
的圖形是否會給我們一些啟發呢?很遺憾,由於f是函數項的一個無窮級數,我們只能停留於畫出部分函數和的圖形。例如,我們在圖9-8中僅畫出第3個部分和
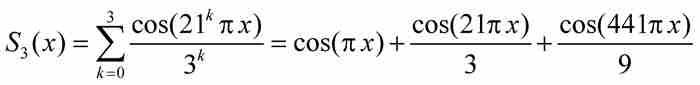
的圖形。這個圖形顯示出大量的方向改變以及某種急劇上升和下降的特性,但是沒有尖角。事實上,魏爾斯特拉斯函數的任何部分和只包含有限的餘弦項,因而是處處可微的。無論畫出哪個部分和的圖形,我們都不能從中找到一個角點。然而,當我轉向求極限產生f本身時,必定處處出現角點。魏爾斯特拉斯函數超出我們直覺所能理解的範圍,是遠非可以用幾何圖形畫在黑板上的。但是從上面的證明看出,它的存在是毋庸置疑的。
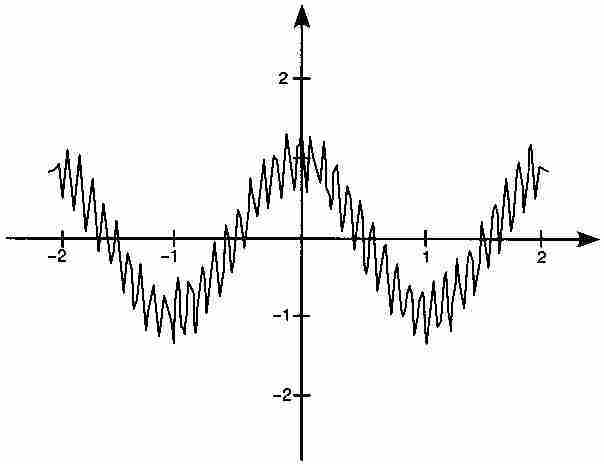
圖 9-8
對於魏爾斯特拉斯這個論證的最後一個反應必然是為它的高度嚴格的標準喝采。猶如一位音樂大師指揮一支著名的管絃樂隊,魏爾斯特拉斯把基本定義、絕對值以及大量的不等式融合成一個協調的整體。在他的證明中,看不出任何處理是隨心所欲的,不存在絲毫憑直覺的痕跡。所以後代的分析學家們對他的最高讚譽是這個證明展現了「魏爾斯特拉斯的嚴格性」。
毫無疑問,對於一個如此病態的函數,並非人人都會感到興奮。某些批評者毅然反對存在一個把不等式作為對付直覺的王牌的數學世界。我們在前面一章介紹過的查爾斯·埃爾米特,對於這個發現黯然神傷,哀歎道:「從這場令人惋惜的沒有導數的函數災難中,我深感震驚和恐怖」。3 亨利·龐加萊(1854—1912)把魏爾斯特拉斯舉出的病態函數的例子稱為「一種對常識的蹂躪」。4 受到的觸怒的埃米爾·皮卡(1856—1941)則這樣表達他的憤慨:「要是牛頓和萊布尼茨曾經想到連續函數不一定存在導數,…… 他們就無需發明微分法了。」 5 不過,這些彷彿從伊甸園走出來的數學家信以為真的建立在直覺形式和幾何基礎上的微積分已經永遠消失了。
3 引自Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 973。
4 E. Hairer and G. Wanner, Analysis by Its History, Springer- Verlag, 1996, p. 261。
5 引自Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 1040。
但是,魏爾斯特拉斯的推理是嚴密的。只要不拋棄極限、連續性和可微性的定義,或者不拒絕賦予分析學家們引進無限過程的權利,那些批評家就注定要失敗。倘若遇到像一個連續而又無處可微的函數這種直覺上的困難,那麼學者們理應修正他們的直覺,而不是拋棄他們面前的數學。分析學的嚴格性因為柯西而提高,又因為魏爾斯特拉斯而達一個新的頂峰。無論人們是否喜歡它,逆轉終歸是不可能的。
在持續不斷的起伏中,數學家們建立起雄偉的理論體系,然後尋找足以揭示他們的思想界限的恰當反例。這種理論與反例的對照成為正確推理的引擎,憑借這種工具,數學得以進步。因為我們唯有知道某些特性是如何喪失的,方能瞭解它們是怎樣發揮作用的。同樣,我們唯有認清直覺是如何把人引入歧途的,方能如實地評價推理的威力。
