第11章 康托爾

格奧爾格·康托爾（1845—1918）

格奧爾格·康托爾於1883年寫下這樣的名句：「數學的本質在於它超然的自主性。」 1 在數學家中很少有人如此徹底地信奉這個原則，也很少有人像康托爾那樣如此從根本上改變了這門學科的性質。Joseph Dauben在對康托爾著作的研究中，把他描繪成「數學史上最富於想像力的和最有爭議的人物之一」。2 在這一章，我們要證實這種評價為什麼說是公允的。

1 Georg Cantor, Gesammelte Abhandlungen, Georg Olms Hildesheim, 1962, p. 182。

2 Joseph Dauben, Georg Cantor: His Mathematics and Philosophy of the Infinite, Princeton University Press, 1979, p. 1。

康托爾出生在一個音樂世家，在他的性情中，更多的是浪漫的藝術家那一面，而不是務實的技術專家這一面。他從事的研究工作最終使他超越數學領域而進入形而上學和神學的疆界。他提出了很多驚世駭俗的論斷。例如，他聲稱莎士比亞的真作是弗朗西斯·培根寫成的；再有，他認定自己關於無窮性的理論證明了上帝的存在。康托爾堅定不移地鼓吹這樣一些信念，使他走上一條疏遠支持者和助長反對者的道路。

與此同時，他在生活中也遇到麻煩。他曾一次又一次地遭受嚴重抑鬱症的折磨，以至最後釀成反覆發作的躁狂抑鬱症，使他喪失一向追求的「精神活力」。3 康托爾一次又一次地被送往人們通常所說的神經病院，在那裡接受他們提供的治療。康托爾於1918年病逝在一家精神病醫療機構，走完了他鬱鬱寡歡的人生路。

3 Joseph Dauben, Georg Cantor: His Mathematics and Philosophy of the Infinite, Princeton University Press, 1979, p. 136。

這樣的坎坷無損於康托爾在數學上取得成功。儘管遭遇不幸，他依然徹底改變了這門學科，而數學的自主性是康托爾情有獨鍾的。

實數的完備性

青年時代的康托爾就讀於柏林大學，成為魏爾斯特拉斯的門生。在學習期間，他於1867年寫了一篇關於數論的專題論文，這是一個完全不同於後來使他聞名於世的領域。他的研究工作把它引向傅裡葉級數並且最終轉到分析學的基礎理論。

正如我們所知，19世紀把微積分的研究直接建立在極限的基礎之上。這時已經清楚地看到，極限本身要依賴於實數系的性質，其中最為重要的一個性質就是我們現在所說的完備性。如今，學生們可能接觸到以不同形式表達的實數的完備性，然而它們在邏輯上是等價的，例如：

C1　任何有界的非減序列收斂於某個實數；

C2　任何柯西序列存在極限；

C3　任何具有上界的非空實數集有一個上確界。

對於需要快速回憶的讀者，我們提醒一下，一個柯西序列{x_k}是指對於每個ε > 0，存在一個正整數N，只要m和n是大於或者等於N的正整數，就有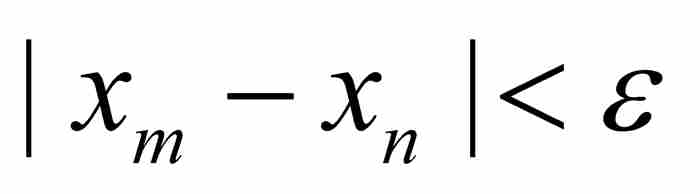。換句話說，柯西序列是這樣一種序列，它們的項之間變得越來越接近並且保持下去。我們在第6章簡要地陳述過這種思想。

同樣，稱M為一個非空集合A的上界，是指對於A中的所有元素a，有a≤M；稱λ為A的最小上界或者上確界，是指(1) λ是A的一個上界，(2) 如果M是A的任意上界，那麼λ ≤M。對於這些概念，任何一本數學分析教科書中都介紹過。

還有一種用區間套術語定義的完備性，它在下面幾章中將扮演一個重要角色。此外，為了闡明接下來做什麼工作，我們需要幾個定義。

一個閉區間[a, b]嵌套在[A, B]內，是指[a, b]是[A, B]的一個子集。這無異於說滿足條件A≤a≤b≤B。我們進一步假定存在一個有界閉區間的序列，其中每個區間嵌套在它前面那個區間內，如像[a_{1, b1] ⊇ [a2, b2] ⊇ [a3, b3] ⊇…⊇ [ak, bk] ⊇…。這樣一個區間序列稱為遞減序列。利用這種序列我們可以引進實數完備性定義的另外一種形式：}

C4　任何有界閉區間的遞減序列必定有同屬於所有區間的公共點。

值得回顧一下，為什麼我們討論的區間必需同時是閉區間和有界區間。請看，閉區間（但不是有界區間）的遞減序列

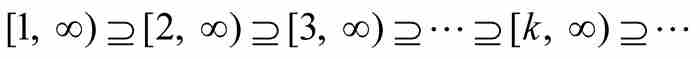
沒有同屬於它們之中所有區間的點；同樣，有界區間（但不是閉區間）的遞減序列

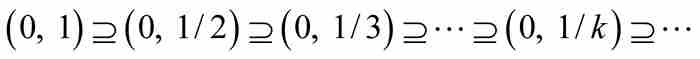
（用集合論中的術語）只有一個空的交集。儘管在19世紀，分析學界的前輩們通常忽略這樣的差別，不過我們在應用C4之前而準備的區間將同時為閉區間和有界區間。

在實數完備性的這四種體現形式中，每一種都保證存在某個實數，它是一個序列收斂的極限，或者成為一個集合所具有的最小上界，或者是一個嵌套區間集中所有區間的公共點。在數學家們探索微積分的邏輯基礎的過程中，他們認識到，這種存在對於他們在理論上追求的目標而言通常已經足夠了。無須明確地求出一個實數，只要得知某處存在一個實數可能就足夠了。實數的完備性所提供的就是這種保證。

人們也許會問：實數的完備性既然如此重要，那麼我們如何證明這種性質的存在？為了回答這個問題，需要數學家們對實數系本身瞭如指掌。從自然數出發，一項直接的任務是定義整數，包括正整數、負整數和數零，再從整數定義有理數。但是我們能夠從更基本的數系建立實數嗎，正如通過整數定義有理數那樣？

對於這個問題，給出肯定回答的是康托爾，同時，他的朋友理查德·戴德金（1831—1916）也獨立地給出這種回答。

康托爾的實數系的結構以有理數的柯西序列的等價類為基礎。戴德金的方法則採用把有理數分為不相交類的劃分，也就是通常所說的「戴德金分割」。對於這些問題的徹底討論將會使我們遠離正題，對本書而言，用有理數構造實數是一個略微深奧的主題，而且對大多數分析學教程來說，這實際上也是頗為神秘的。然而，康托爾和戴德金成功地完成了這種構造，然後運用他們的思想證明實數的完備性，作為他們新開闢的領域的一個定理。

可以把這個成就視為微積分同幾何學分離的決定性步驟。戴德金和康托爾最終回歸到算術的基礎——自然數，由此到達實數，然後證實它的完備性，而最終使全部分析學得以建立起來。他們取得的這個成就使他們兩人獲得一個貼切的但是拗口的綽號：「分析學的算術化家」。

區間的不可數性

康托爾在1874年寫了一篇題為「論全體實代數數的總體性質」的論文。1 在這篇文章中他採用「區間的不可數性」作為標題，選擇這個標題並不是為了定義實數。這是數學史上的一座里程碑，用Joseph Dauben的話說，這展示了康托爾「對於提出深刻的問題以及不時探索始料未及的解法以至尋求非正統答案的天賦」。2

1 Georg Cantor, Gesammelte Abhandlungen, Georg Olms Hildesheim, 1962, pp. 115-118。

2 Joseph Dauben, Georg Cantor: His Mathematics and Philosophy of the Infinite, Princeton University Press, 1979, p. 45。

很奇怪，這篇論文的重要意義被它的標題掩蓋了，因為關於代數數的結果只不過是文章的真正革命性思想的一個推論，儘管是最有價值的推論。簡單地說，這個思想就是一個序列不能窮舉一個開區間中的全部實數。正如我們將會看到的那樣，康托爾的論證包含了實數的完備性性質，因此把它放在實分析的領域是恰當的。

定理　如果{x_k}是不同實數的一個序列，那麼實數的任何有界開區間（α, β）含有不包括在{x_k}中的一點。

證明　工康托爾從一個區間（α, β）開始，並且按照連貫的次序x_{1, x2, x3, x4, …考察序列。如果在這些項中沒有一個或者僅有一個落入（α, β）內的無窮多實數中間，那麼定理顯而易見是正確的。}

撇開這種情況不談，假定區間（α, β）至少包含序列中的兩個點。這時我們來確定其中的前面兩項，即具有最小下標的兩項。我們用A_{1表示較小的項，用B1表示較大的項。這個步驟在圖11-1中說明。請注意，序列的起初幾項落在（α, β）之外，但是x4和x7落到區間內。按照我們的定義，A1 = x7（較小的項），B1 = x4（較大的項）。}

圖　11-1

我們作兩點簡單然而非常重要的說明：

1. α < A_{1 < B2 < β；}

2. 如果某個序列項x_k落入開區間（A_{1, B1）內，那麼k ≥3。}

上面第二個結論認定，在確定A_{1和B1時至少要用到序列的兩個項，所以嚴格位於A1和B1之間的項必須具有k = 3或者k > 3的下標。在圖11-1中，下一個這種候選項將是x8。}

康托爾然後檢查區間（A_{1, B1）並且考慮同樣的兩種情形：這個開區間不包含序列{xk}中的任何項或只包含{xk}的一項；或者（A1, B1）至少包含{xk}中的兩項。在第一種情形，定理是成立的，因為在（A1, B1）中，因而在（α, β）中，存在無窮多不屬於序列{xk}的其他點。在第二種情形，康托爾重複原先的過程，選擇序列中接下來的兩項，即落入區間（A1, B1）的具有最小下標的兩項。他把其中較小的項標記為A2，較大的項標記為B2。如果我們考查圖11-2（圖中包含比圖11-1更多的序列項），看出A2 = x10和B2 = x11。}

圖　11-2

在此顯然也有兩個結果：

(1) α < A_{1 < A2 < B1 < B2 < β；}

(2) 如果x_k落入開區間（A_{2, B2）內，那麼k ≥5。}

同前面一樣，得出第二個結果是因為在求A_{1，B1和A2，B2時必須用到序列{xk}中的四個項。}

康托爾繼續採用這種方式。在任何一步，如果在開子區間內只剩下序列的一項或者沒有序列的項，那麼他能夠立即求出屬於（α, β）但是不屬於序列{x_k}的一點——實際上存在無窮多這樣的點。唯一潛在的困難將出現在這個過程永不終止時，這種情況下會產生這樣兩個無窮序列{A_r}和{B_r}：

1. α < A_{1 < A2 < A3 < … < Ar < … < Br< … < B3 < B2 < B1 < β；}

2. 如果x_k落入開區間（A_r, B_r）內，那麼k ≥ 2 r + 1。

這樣一來，我們得到一個閉有界區間的序列[A_{1, B1] ⊇ [A2, B2] ⊇ [A3, B3] ⊇…，其中每個區間嵌套在它前面的一個區間內。根據實數的完備性（C4），至少存在所有區間[Ar, Br]的一個公共點。就是說，存在一點c屬於所有r ≥1的區間[Ar, Br]。為了最終完成證明，我們只需要確定c落入區間（α, β）之中而又不是序列{xk}的一項。}

我們立即證實第一個結論，因為c是在[A_{1, B1]⊂（α, β）中，所以c確實落入原來的開區間（α, β）之內。}

至於第二點，c有可能是序列{x_k}的一項嗎？如果可能，那麼對於某個下標N有c = x_N。由於c落入所有閉區間內，它必定落入[A_{N+1，BN+1]內，因此}

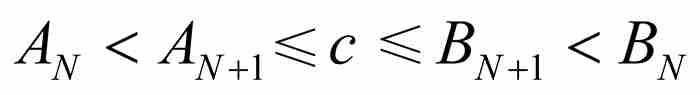
由此推出c = x_N落入開區間（A_N, B_N）內，所以根據上面第(2) 個結果，N≥2 N+1。自然，這是荒謬的。我們由此推斷c不可能是序列{x_k}中的項。

總之，康托爾證實了在區間（α, β）內存在不出現在原來序列{x_k}之中的一點，這就是定理要證明的結果。

而今，在這個定理前面通常要加上少許術語。如果一個集合同自然數集之間能夠一一對應，我們把它定義為可數集。序列顯然是可數的，因為所需的對應表現為下標同自然數的對應。不能同自然數集一一對應的無窮集稱為不可數集。於是，我們把上述結果的特徵描述為實數的任何開區間是不可數的。

康托爾關於這個問題的思想演變是很有趣的。在整個19世紀70年代初期，他都在冥思苦索實數的基本性質，試圖建立完全同有理數分離的實數。顯而易見，完備性是一個關鍵性的差別，這種性質在某種程度上體現了由實數的「連續統」所指的意思。

但是康托爾開始猜測這兩種集合在元素數量的充裕性上存在差異，如今我們把這種充裕性稱為它們的「基數性」。康托爾於1873年11月，把他對自然數同實數可能以某種一一對應方式匹配的懷疑告訴戴德金。這個懷疑隱含這樣的意思，儘管兩種集合都是無限的，但是實數集的元素要多得多。

在經過所有可能的嘗試後，康托爾未能對他的直覺猜測提供證明。他帶著某種受挫的心理寫信給戴德金說：「我異常強烈地傾向於這樣一種判斷，在自然數同實數之間不容許出現這樣的一一對應，但是我沒有找到理由。」 3 僅在一個月之後，康托爾取得了一次突破。他把他的證明作為一份聖誕節禮物寄給戴德金，並且在收到這位朋友的建議後加以整理和發表，這就是我們在上面所見的證明。持久不懈的探索終究獲得報賞。

3 Joseph Dauben, Georg Cantor: His Mathematics and Philosophy of the Infinite, Princeton University Press, 1979, p. 49。

對於康托爾後來關於非可數性的「對角化」證明有所瞭解的讀者，可能會驚奇地發現，他在1874年給出的推理是全然不同的。對角化論證出現在康托爾1891年的一篇論文中，他把它描述為一種「非常簡單的證明」。4 正如我們所見，在1874年的證明中引用了完備性性質，而對角化證明適用於與完備性不相干的情形，完全不同於真正的分析約束條件。

4 Georg Cantor, Gesammelte Abhandlungen, Georg Olms Hildesheim, 1962, p. 278。

雖然後一種論證更為常見，但是前一種論證代表歷史的開端，所以在這裡介紹它。我們再次強調，康托爾當初的證明沒有使用像可數性一類的術語，也未提出關於無限基數的特別問題。所有這些都是後來引進的。在1874年，他只證明了一個序列不可能窮舉一個開區間。

但是，為什麼任何人都應予關注呢？這是一個很有價值的問題，而康托爾得到了一個引人注目的答案。

再論超越數的存在

回憶一下，康托爾的論文所冠的標題是「論全體實代數數的總體性質」。到這時，已經提到了代數數，但是對於這個標題所指的這些數的「特性」尚未作任何說明。現在到了澄清這些遺漏問題的時候了。

我們已經知道，如果一個實數是某個整係數多項式方程的解，那麼它是代數數。有無窮多這樣的數（例如任何有理數），並且對於劉維爾來說，尋找置身於這個代數數家族之外的一個數，曾經是一件非常困難的事情。

在對這個問題深思熟慮的基礎上，康托爾斷言可能用一個序列列舉出這種代數數。乍看起來，這似乎是十分荒謬的結論。為了證實他的斷言，需要生成具有兩個密切相關性質的一個序列：(1) 序列的每一項都是代數數，(2) 每個代數數均處於序列的某個位置上。要做到這一點，一種聰明的方法必然是採用某種有序的和窮舉的方式，然而康托爾似乎不那麼聰明。他卻從引進一種新思想入手。

定義　如果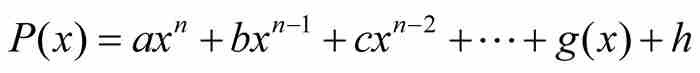是一個整係數n次多項式，我們把它的高度定義為。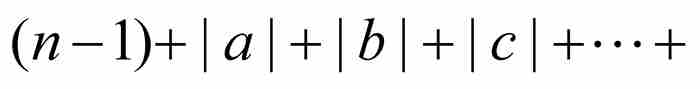

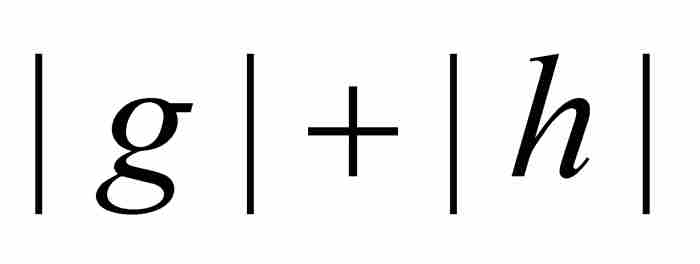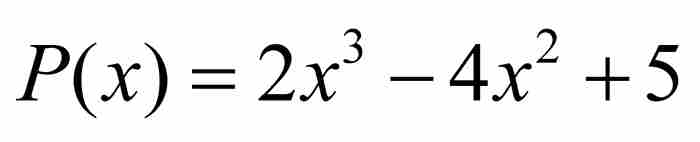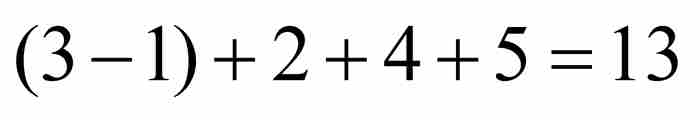例如，的高度為，而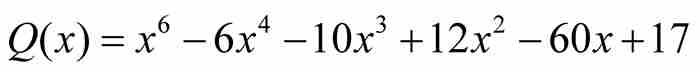的高度為(6 - 1) + 1 + 6 + 10 + 12 + 60 + 17 = 111。

顯然，一個整係數多項式的高度必定是一個自然數。不僅如此，任何代數數有一個次數最小的多項式，我們可以假定在它的係數之間不存在除1之外的公因數。這些約定將會簡化即將提出的任務。

康托爾依次收集全部代數數：首先是高度為1的多項式產生的代數數，其次是高度為2的多項式產生的代數數，然後是高度為3的多項式產生的代數數，如此進行下去。這樣做是把代數數排列成一個無窮序列的關鍵步驟，在此用{a_k}表示這個序列。

為了看清這個操作過程，我們注意高度為1的唯一的整係數多項式是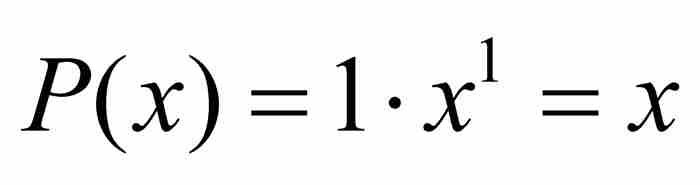。相應的方程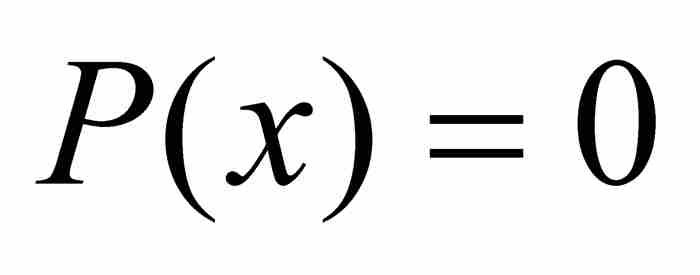的解是第一個代數數，即 。

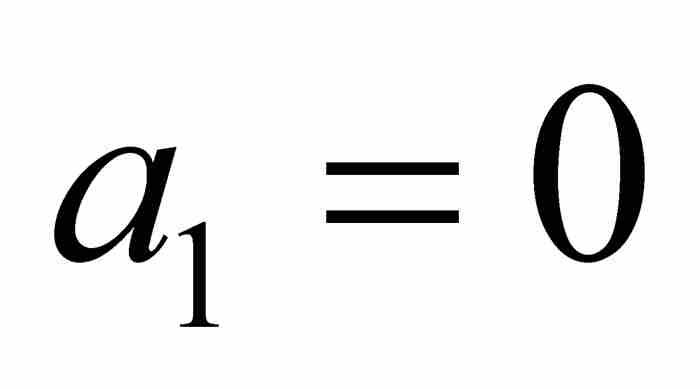高度為2的多項式共有4個：

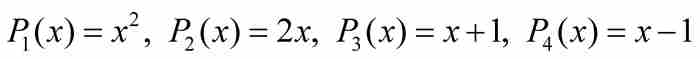
置其中第一個和第二個多項式為零，產生解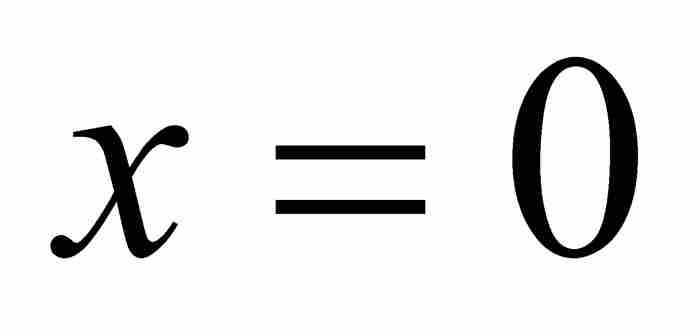，我們不再考慮這個解。置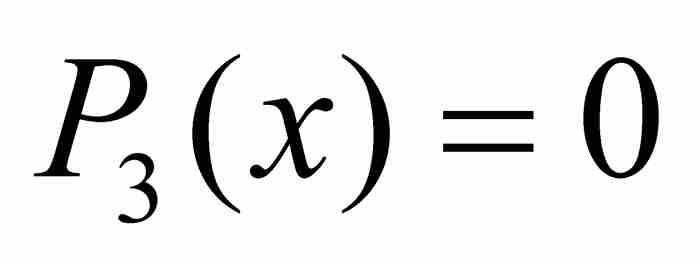，給出第二個代數數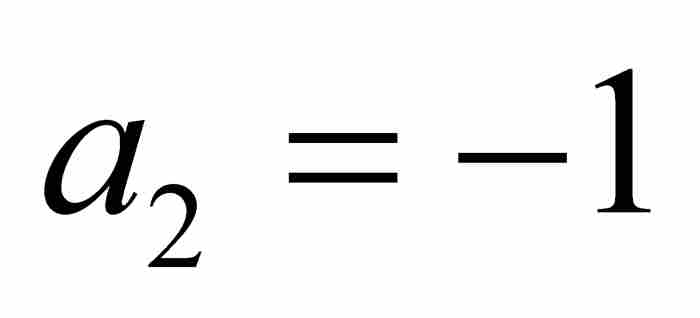；置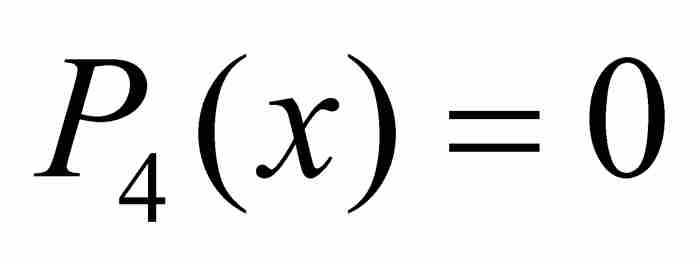，給出第三個代數數。

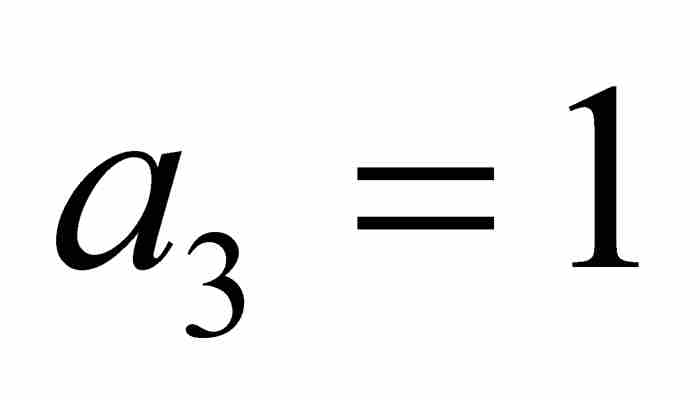我們繼續進行。高度為3的多項式共有11個：

,

,

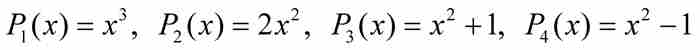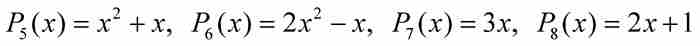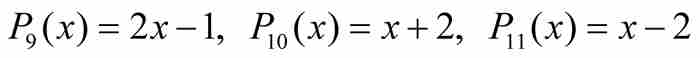
當置這些多項式為零時，我們求解出4個新的代數數：

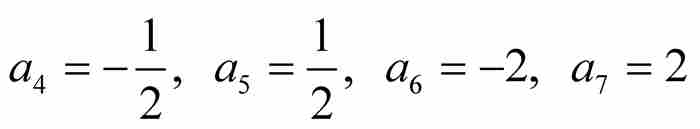
正如康托爾在其文章的標題中指出的那樣，他的關注點僅限於實代數數，所以方程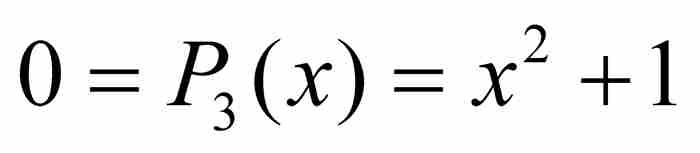的複數解對這個集合不添加新元素。

我們再往下進行。高度為4的多項式共有28個，從這些多項式可獲得另外12代數數，其中有幾個是無理數。例如，多項式是高度為4的多項式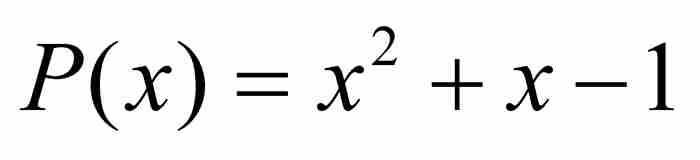，由它產生的代數數是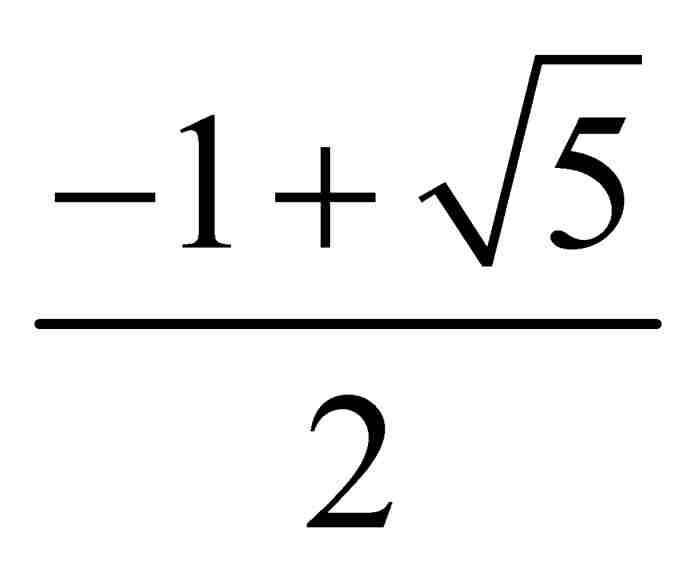和。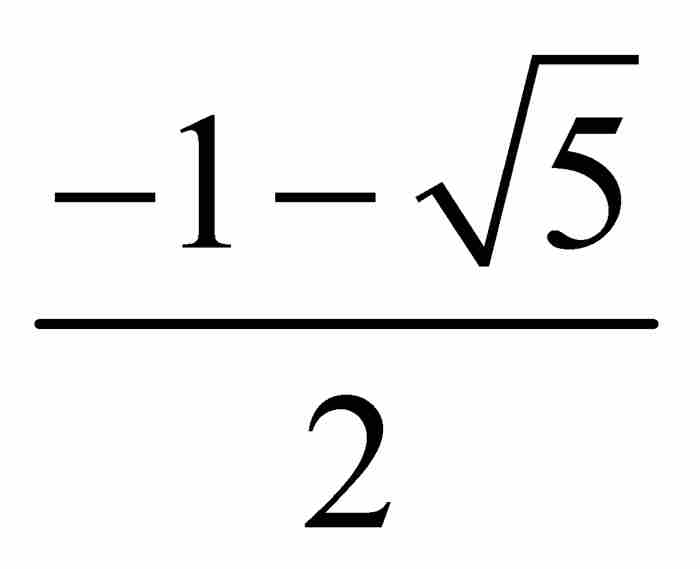

隨著多項式高度的增加，將產生越來越多的代數數。反過來說，任何一個特定的代數數，必定出自某個整係數多項式，而這個多項式本身具有某個高度。例如，我們在第8章遇到的代數數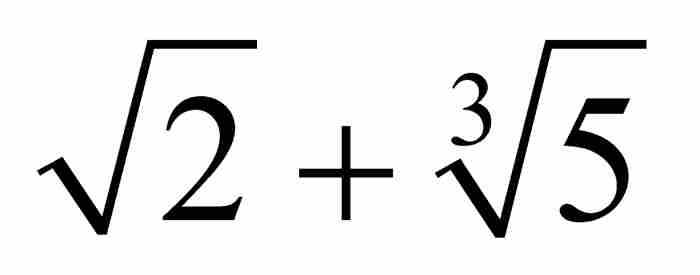是多項式方程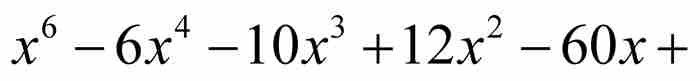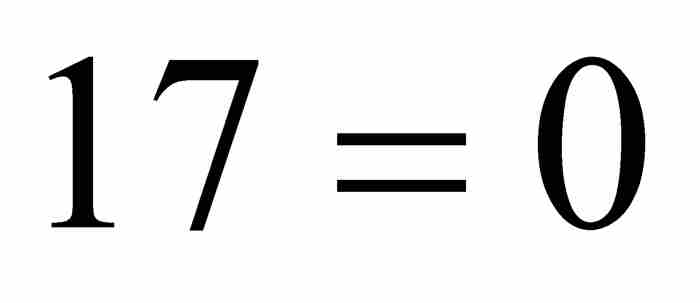的一個解，這個多項式的高度為111。

下面所作的幾點簡單說明使康托爾得以完成他的論證：

• 對於一個給定的高度，僅存在有限個整係數多項式。

• 每個這樣的多項式僅可能產生有限個代數數（因為一個n次多項式方程具有的解不會超出n個）。

• 因此，對於每個高度，僅可能添加有限個新的代數數。

這就意味著，在尋找代數數的過程中，當我們從一個給定的高度「進入」時，必定在有限步之後從那個高度退出。我們不可能「陷進」這個高度的深淵，在那裡試圖列舉出無限個代數數。

由此可見，具有多項式高度111的代數數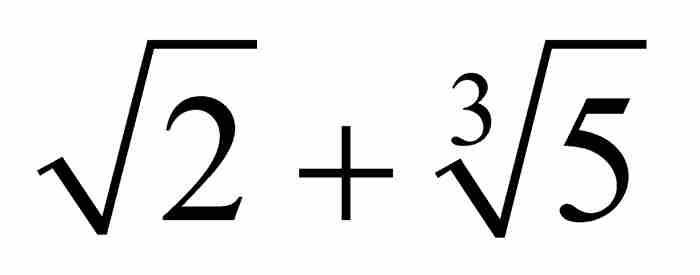必定在序列{a_k}中的某處出現。當然，確定它在序列中的位置還要花費一些時間，但是這個過程必定在有限步之後把我們引向到高度111，然後在遍歷這個高度的多項式過程中，再經過有限步之後到達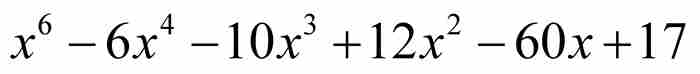。這將會決定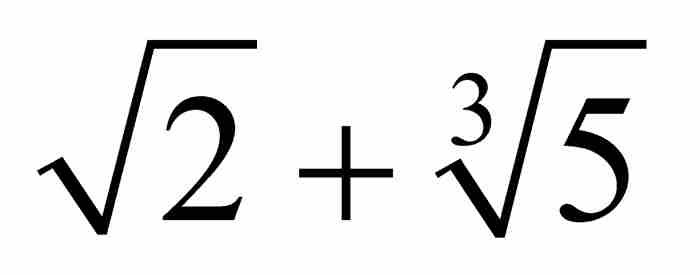在序列{x_k}中的位置。對於任何一個實代數數，我們可以作出同樣的論斷。所以，在康托爾的文章標題中提及的代數數的那個「總體特性」，按照現代的說法就是代數數的「可數性」。

至此，康托爾把他獲得的兩個結果結合起來：首先，一個序列不可能窮舉一個區間中的全部點；其次，所有代數數構成一個序列。單獨而言，這兩個結果都是很有趣的。把它們結合在一起，更使他能夠推斷所有代數數不會佔據一個開區間上的全部點。因此，在任何一個開區間（α, β）內，必定存在一個超越數。

或者，可以直截了當地說存在超越數。

自然，這是劉維爾在幾十年之前已經論證的結果，那時他證明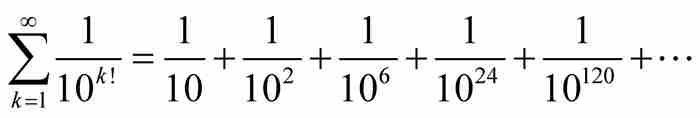是超越數。為了證實超越數的存在，劉維爾不懈地努力並且找到了一個超越數。

康托爾通過完全不同的方法達到同一目標。他早在1874年發表的論文中就曾許諾「對劉維爾首次證明的定理給出一個新的證明」，無疑他實踐了自己的諾言。1然而，正如我們所見，在他的論證中沒有包含一個特定超越數的例子。這顯然是一種非直接的證明。

1 Georg Cantor, Gesammelte Abhandlungen, Georg Olms Hildesheim, 1962, p. 116。

為了對比這兩種證明方法，我們用在一個乾草堆中尋找一根針來作類比。我們可以想像，極端勤勞的劉維爾，穿上他的舊衣衫，徒步來到田間，在炎炎烈日之下圍繞乾草堆四處翻騰。幾個小時過去了，他汗流浹背，逃避的獵物——一根針突然刺痛了他的手指。相形之下，康托爾則從容不迫，躲在屋子裡運用純粹的邏輯推理方法，證明乾草堆的質量超過其中乾草的質量。他由此推斷乾草堆中一定還隱藏著別的東西，就是說，質量的超出是由一根針引起的。不像劉維爾那樣，康托爾依然涼爽如初和一塵不染。

有些數學家受到一種非結構性證明的困擾，這種證明依賴於無窮集合的性質。同劉維爾所做的冗長論證相比，康托爾的證明則顯得過於容易，幾乎像變戲法一樣。年輕的伯特蘭·羅素（1872—1970）對於康托爾的思想作出的第一反應，在數學家當中也許不是絕無僅有的。他在其自傳中寫道：

我曾經花費很長時間研究格奧爾格·康托爾的論文，並且把他論述的各種要點記到一個筆記本中。那時，我錯誤地認為他所作的全部論證在邏輯上是謬誤的。儘管如此，我仍然從最微小的細節上深入考察了他的全部證明。後來，當我發現所有謬誤竟然屬於自己時，這反倒令我獲益匪淺。2

2 Bertrand Russell, The Autobiography of Bertrand Russell, vol. 1, Allen and Unwin, 1967, p. 127。

像羅素一樣，數學家們對於作為一位革新者的康托爾給予高度讚揚。他在1874年發表的那篇論文開創了分析學的一個新時代，其中集合論思想在應用上同魏爾斯特拉斯發明的ε - δ 方法並駕齊驅。

康托爾的工作取得許多重要結果，其中不少確實令人驚歎。例如，很容易證明，如果代數數和超越數都是可數的，那麼它們的並集，即全體實數的集合，必然也是可數的。由於這個結論是不正確的，康托爾由此識破超越數構成一個不可數的集合，因此在數量上遠遠超過它們的「表親」代數數。對於這兩種數的多寡之分，Eric Temple Bell給出這樣的描述：「代數數猶如鑲嵌在長空夜幕下的點點繁星，而濃黑的萬里長空則是超越數的蒼穹。」 3 這是一種令人陶醉的難以想像的感受，因為充足的數似乎是稀疏的，而稀疏的數似乎是充足的。在一定的意義上，康托爾證明了超越數是乾草堆中的乾草而不是掉進草堆中的針。

3 Eric Temple Bell, Men of Mathematics, Simon & Schuster, 1937, p.569。

還有一個相關的但意義更深遠的結果，那就是 「小」無窮集合同「大」無窮集合之間的區別。康托爾證明了，一個可數集儘管是無窮的，然而當把它和不可數集相比時，它的無窮性卻是無足輕重的。隨著他的思想的確立，數學家們逐漸認識到，在解決重要問題中，如此不值一提的可數集無疑是值得使用的。

我們將會看出，小集合和大集合之間的對立也會出現在其他的分析學環境中。在19世紀初，勒內·貝爾發現了一種「大」與「小」的對比，這種分歧出現在他所說的集合的「類型」中，而亨利·勒貝格在他稱為「測度」的度量中發現了另外一種對比。雖然基數、類型和測度是不同範疇的概念，但是它們都提供一種比較集合的手段，在數學分析中被證實是很有價值的。

康托爾還致力於解決有關無窮集合的其他問題。其中之一是：「存在比區間的基數更大的不可數集嗎？」關於這個問題他給出肯定的回答。另外一個問題是：「存在基數介於可數序列和不可數區間之間的一種無窮集合嗎？」在解決這個問題時，他沒有取得成功。由於康托爾的遠見卓識和不斷的研究，集合論迎來了它自身的發展時期，在這個階段它完全脫離固有分析學所關注的問題。不過，這一切都源於1874年康托爾所寫的那篇論文。

同許多推翻歷史的革命家不一樣，康托爾在有生之年親眼見到他的思想被廣大學術界接受。一位最早的推崇者是上面提到羅素，他把康托爾描繪為「19世紀最偉大的知識分子之一」。4 這是出自一位數學家、哲學家和諾貝爾獎得主的非同尋常的讚譽。

4 Bertrand Russell, The Autobiography of Bertrand Russell, vol. 1, Allen and Unwin, 1967, p. 217。

康托爾的另外一位讚頌者是意大利的數學奇才維托·沃爾泰拉。他的工作將魏爾斯特拉斯的分析學同康托爾的集合論巧妙地結合在一起，這正是我們在下面一章要討論的主題。