線性代數中最基本的數據類型是矩陣。矩陣由行和列組成。
圖B-1給出了一個簡單的矩陣樣例。該矩陣由3行3列組成。行通常從上到下編號,而列則從左到右編號。第一行的值分別是9、9和77。類似地,第3列的值分別是77、18和10。在NumPy當中可以通過調用numpy.shape(myMat)來得到給定矩陣myMat的行列大小。上述調用返回的結果形式是(行數,列數)。

圖B-1 一個簡單的3x3矩陣,圖中給出了行、列的方向
本書每一章都用到了向量,而向量是一個特殊的矩陣,其行或列數目為1。通常情況下,提到向量時不會特別說是行向量還是列向量。如果這樣,則假設是列向量。圖B-2左部給出了一個列向量,是一個3×1的矩陣。而在圖B-2右部給出的是一個1×3的行向量。在矩陣的運算過程中跟蹤矩陣的大小十分重要,比如矩陣乘法。

圖B-2 左邊給出了一個列向量,右邊給出了一個行向量
矩陣的一個最基本的運算是轉置,即按照對角線翻轉矩陣。原來的行變成列、列變成行。圖B-3給出了矩陣B的一個轉置過程示意圖。轉置運算通過矩陣上標的一個大寫的T來表示。轉置運算常用來對矩陣處理使之更加容易計算。
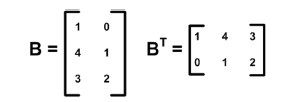
圖B-3 矩陣的轉置過程,轉置後行變成列
可以用一個數字去加或者乘以矩陣,這相當於對矩陣的每個元素都獨立進行加法或乘法運算。由於矩陣元素之間的相對值沒有發生變化,而只有比例發生了變化,所以上述這類運算稱為標量運算(scalar operation)。如果想對矩陣進行常數放縮變換或者加上一個常數偏移值,就可以使用矩陣標量乘法或加法運算。圖B-4給出了標量乘法和加法的兩個例子。

圖B-4 矩陣上的標量運算,最後的結果是每個元素乘上或者加上某個標量
接下來看一些矩陣運算。如何對兩個矩陣求和?首先,兩個矩陣行列數必須要相同才能進行求和運算。矩陣求和相當於每個位置上對應元素求和。圖B-5給出了一個例子。矩陣減法運算與此類似,只不過將剛才的加法變成減法即可。

圖B-5 矩陣求和
一個更有趣的運算是矩陣乘法。兩個矩陣相乘不像標量乘法那麼簡單。兩個矩陣要相乘,前一個矩陣的列數必須要等於後一個矩陣的行數。例如,兩個分別為3×4和4×1的矩陣可以相乘,但是3×4的矩陣不能和1×4的矩陣相乘。而3×4的矩陣和4×1的矩陣相乘會得到3×1的結果矩陣。有一種方法可以快速檢查兩個矩陣能否相乘以及結果矩陣大小,將它們的大小連在一起的寫法 (3×4)(4×1)。由於中間的值相等,因此可以進行乘法運算。去掉中間的值之後,就可以得到結果矩陣的大小3×1。圖B-6給出了一個矩陣乘法的例子。

圖B-6 一個矩陣乘法的示意圖,圖中3x2矩陣乘以2x1矩陣得到一個3x1矩陣
本質上來說,圖B-6中所做的是將3×2矩陣的每一行旋轉之後與2×1矩陣的每一列對齊,然後計算對應元素的乘積並最終求和。矩陣相乘還可以看成是列的加權求和(參見圖B-7)。

圖B-7 矩陣乘法可以看成是列的加權求和
在上面第二種看法下,最終的結果雖然一樣但是採用了不同的組織方式。將矩陣乘法看成是列加權求和對於某些算法很有用,比如矩陣相乘的MapReduce版本。一般來說,兩個矩陣X和Y的乘法定義為:

如果對上述兩種做法的一致性存疑,那麼總是可以採用上式來對矩陣求積。
機器學習中的一個常用運算是對向量求內積(也稱點積)。比如第6章支持向量機中就需要對向量進行內積計算。兩個向量進行內積計算時,相應元素相乘然後求和得到最終向量。圖B-8給出了一個示意圖。

圖B-8 兩個向量的內積計算
通常來說,向量內積還有一層物理含義,比如某個向量沿著另一個向量的移動量。向量的內積可以用於計算兩個向量的夾角餘弦值。在任意支持矩陣乘法的程序中,可以通過X的轉置乘以Y實現兩個向量X和Y的內積計算。如果向量X和Y的長度都是m,那麼兩個向量都可以看成m×1的矩陣,因此XT是1×m的矩陣,XT*Y是1×1的矩陣。
