線性回歸
優點:結果易於理解,計算上不複雜。 缺點:對非線性的數據擬合不好。 適用數據類型:數值型和標稱型數據。
回歸的目的是預測數值型的目標值。最直接的辦法是依據輸入寫出一個目標值的計算公式。假如你想要預測姐姐男友汽車的功率大小,可能會這麼計算:
HorsePower = 0.0015*annualSalary - 0.99*hoursListeningToPublicRadio
這就是所謂的回歸方程(regression equation),其中的0.0015和-0.99稱作回歸係數(regression weights),求這些回歸係數的過程就是回歸。一旦有了這些回歸係數,再給定輸入,做預測就非常容易了。具體的做法是用回歸係數乘以輸入值,再將結果全部加在一起,就得到了預測值1。
1. 此處的回歸係數是一個向量,輸入也是向量,這些運算也就是求出二者的內積。——譯者注
說到回歸,一般都是指線性回歸(linear regression),所以本章裡的回歸和線性回歸代表同一個意思。線性回歸意味著可以將輸入項分別乘以一些常量,再將結果加起來得到輸出。需要說明的是,存在另一種稱為非線性回歸的回歸模型,該模型不認同上面的做法,比如認為輸出可能是輸入的乘積。這樣,上面的功率計算公式也可以寫做:
HorsePower = 0.0015*annualSalary/hoursListeningToPublicRadio
這就是一個非線性回歸的例子,但本章對此不做深入討論。
回歸的一般方法
- 收集數據:採用任意方法收集數據。
- 準備數據:回歸需要數值型數據,標稱型數據將被轉成二值型數據。
- 分析數據:繪出數據的可視化二維圖將有助於對數據做出理解和分析,在採用縮減法求得新回歸係數之後,可以將新擬合線繪在圖上作為對比。
- 訓練算法:找到回歸係數。
- 測試算法:使用R2或者預測值和數據的擬合度,來分析模型的效果。
- 使用算法:使用回歸,可以在給定輸入的時候預測出一個數值,這是對分類方法的提升,因為這樣可以預測連續型數據而不僅僅是離散的類別標籤。
「回歸」一詞的來歷
今天我們所知道的回歸是由達爾文(Charles Darwin)的表兄弟Francis Galton發明的。Galton於1877年完成了第一次回歸預測,目的是根據上一代豌豆種子(雙親)的尺寸來預測下一代豌豆種子(孩子)的尺寸。Galton在大量對像上應用了回歸分析,甚至包括人的身高。他注意到,如果雙親的高度比平均高度高,他們的子女也傾向於比平均高度高,但尚不及雙親。孩子的高度向著平均高度回退(回歸)。Galton在多項研究上都注意到這個現象,所以儘管這個英文單詞跟數值預測沒有任何關係,但這種研究方法仍被稱作回歸2。
2. Ian Ayres, Super Crunchers (Bantam Books, 2008), 24.
應當怎樣從一大堆數據裡求出回歸方程呢?假定輸入數據存放在矩陣X中,而回歸係數存放在向量w中。那麼對於給定的數據X1,預測結果將會通過 給出。現在的問題是,手裡有一些
給出。現在的問題是,手裡有一些X和對應的y,怎樣才能找到w呢?一個常用的方法就是找出使誤差最小的w。這裡的誤差是指預測y值和真實y值之間的差值,使用該誤差的簡單累加將使得正差值和負差值相互抵消,所以我們採用平方誤差。
平方誤差可以寫做:
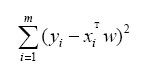
用矩陣表示還可以寫做 。如果對
。如果對w求導,得到 ,令其等於零,解出
,令其等於零,解出w如下:

w上方的小標記表示,這是當前可以估計出的w的最優解。從現有數據上估計出的w可能並不是數據中的真實w值,所以這裡使用了一個「帽」符號來表示它僅是w的一個最佳估計。
值得注意的是,上述公式中包含(XTX)-1,也就是需要對矩陣求逆,因此這個方程只在逆矩陣存在的時候適用。然而,矩陣的逆可能並不存在,因此必須要在代碼中對此作出判斷。
上述的最佳w求解是統計學中的常見問題,除了矩陣方法外還有很多其他方法可以解決。通過調用NumPy庫裡的矩陣方法,我們可以僅使用幾行代碼就完成所需功能。該方法也稱作OLS,意思是「普通最小二乘法」(ordinary least squares)。
下面看看實際效果,對於圖8-1中的散點圖,下面來介紹如何給出該數據的最佳擬合直線。

圖8-1 從ex0.txt得到的樣例數據
程序清單8-1可以完成上述功能。打開文本編輯器並創建一個新的文件regression.py,添加其中的代碼。
程序清單8-1 標準回歸函數和數據導入函數
from numpy import *
def loadDataSet(fileName):
numFeat = len(open(fileName).readline.split(\'t\')) - 1
dataMat = ; labelMat =
fr = open(fileName)
for line in fr.readlines:
lineArr =
curLine = line.strip.split(\'t\')
for i in range(numFeat):
lineArr.append(float(curLine[i]))
dataMat.append(lineArr)
labelMat.append(float(curLine[-1]))
return dataMat,labelMat
def standRegres(xArr,yArr):
xMat = mat(xArr); yMat = mat(yArr).T
xTx = xMat.T*xMat
if linalg.det(xTx) == 0.0:
print \"This matrix is singular, cannot do inverse\"
return
ws = xTx.I * (xMat.T*yMat)
return ws
第一個函數loadDataSet與第7章的同名函數是一樣的。該函數打開一個用tab鍵分隔的文本文件,這裡仍然默認文件每行的最後一個值是目標值。第二個函數standRegres用來計算最佳擬合直線。該函數首先讀入x和y並將它們保存到矩陣中;然後計算XTX,然後判斷它的行列式是否為零,如果行列式為零,那麼計算逆矩陣的時候將出現錯誤。NumPy提供一個線性代數的庫linalg,其中包含很多有用的函數。可以直接調用linalg.det來計算行列式。最後,如果行列式非零,計算並返回w。如果沒有檢查行列式是否為零就試圖計算矩陣的逆,將會出現錯誤。NumPy的線性代數庫還提供一個函數來解未知矩陣,如果使用該函數,那麼代碼ws=xTx.I * (xMat.T*yMat)應寫成ws=linalg.solve(xTx, xMat.T*yMatT)。
下面看看實際效果,使用loadDataSet將從數據中得到兩個數組,分別存放在X和Y中。與分類算法中的類別標籤類似,這裡的Y是目標值。
>>> import regression
>>> from numpy import *
>>> xArr,yArr=regression.loadDataSet(\'ex0.txt\')
首先看前兩條數據:
>>> xArr[0:2]
[[1.0, 0.067732000000000001], [1.0, 0.42781000000000002]]
第一個值總是等於1.0,即X0。我們假定偏移量就是一個常數。第二個值X1,也就是我們圖中的橫坐標值。
現在看一下standRegres函數的執行效果:
>>> ws = regression.standRegres(xArr,yArr)
>>> ws
matrix([[ 3.00774324],
[ 1.69532264]])
變量ws存放的就是回歸係數。在用內積來預測y的時候,第一維將乘以前面的常數X0,第二維將乘以輸入變量X1。因為前面假定了X0=1,所以最終會得到y=ws[0]+ws[1]*X1。這裡的y實際是預測出的,為了和真實的y值區分開來,我們將它記為yHat。下面使用新的ws值計算yHat:
>>> xMat=mat(xArr)
>>> yMat=mat(yArr)
>>> yHat = xMat*ws
現在就可以繪出數據集散點圖和最佳擬合直線圖:
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure
>>> ax = fig.add_subplot(111)
>>> ax.scatter(xMat[:,1].flatten.A[0], yMat.T[:,0].flatten.A[0])
<matplotlib.collections.CircleCollection object at 0x04ED9D30>
上述命令創建了圖像並繪出了原始的數據。為了繪製計算出的最佳擬合直線,需要繪出yHat的值。如果直線上的數據點次序混亂,繪圖時將會出現問題,所以首先要將點按照升序排列:
>>> xCopy=xMat.copy
>>> xCopy.sort(0)
>>> yHat=xCopy*ws
>>> ax.plot(xCopy[:,1],yHat)
[<matplotlib.lines.Line2D object at 0x0343F570>]
>>> plt.show
我們將會看到類似於圖8-2的效果圖。

圖8-2 ex0.txt的數據集與它的最佳擬合直線
幾乎任一數據集都可以用上述方法建立模型,那麼,如何判斷這些模型的好壞呢?比較一下圖8-3的兩個子圖,如果在兩個數據集上分別作線性回歸,將得到完全一樣的模型(擬合直線)。顯然兩個數據是不一樣的,那麼模型分別在二者上的效果如何?我們當如何比較這些效果的好壞呢? 有種方法可以計算預測值yHat序列和真實值y序列的匹配程度,那就是計算這兩個序列的相關係數。

圖8-3 具有相同回歸係數(0和2.0)的兩組數據。上圖的相關係數是0.58,而下圖的相關係數是0.99
在Python中,NumPy庫提供了相關係數的計算方法:可以通過命令corrcoef(yEstimate, yActual)來計算預測值和真實值的相關性。下面我們就在前面的數據集上做個實驗。
與之前一樣,首先計算出y的預測值yMat:
>>> yHat = xMat*ws
再來計算相關係數(這時需要將yMat轉置,以保證兩個向量都是行向量):
>>> corrcoef(yHat.T, yMat)
array([[ 1. , 0.98647356],
[ 0.98647356, 1. ]])
該矩陣包含所有兩兩組合的相關係數。可以看到,對角線上的數據是1.0,因為yMat和自己的匹配是最完美的,而YHat和yMat的相關係數為0.98。
最佳擬合直線方法將數據視為直線進行建模,具有十分不錯的表現。但是圖8-2的數據當中似乎還存在其他的潛在模式。那麼如何才能利用這些模式呢?我們可以根據數據來局部調整預測,下面就會介紹這種方法。
